Giải Toán 8 trang 79 tập 1 Kết nối tri thức
Giải Toán 8 trang 79 Tập 1
Giải Toán 8 trang 79 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 79.
Luyện tập 3 trang 79 Toán 8 tập 1 Kết nối
Tìm các độ dài x, y trong Hình 4.6.
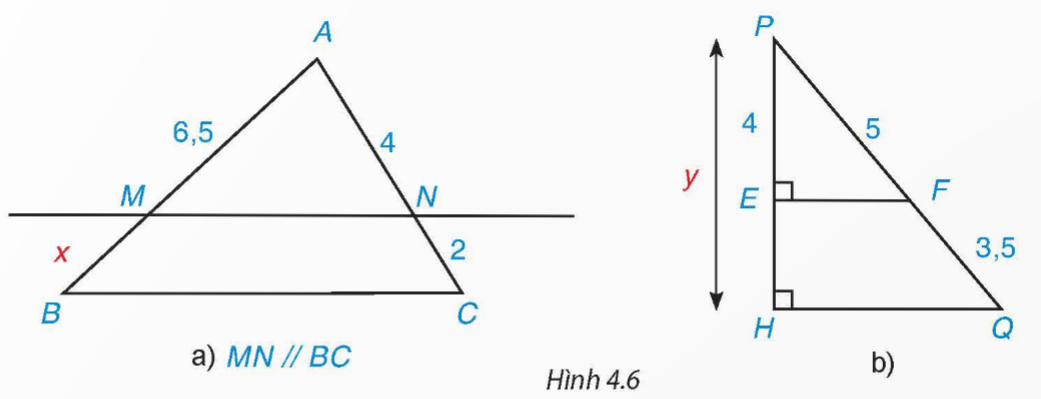
Hướng dẫn giải:
a) Xét tam giác ABC có MN // BC
⇒ 
\(\frac{AM}{MB}=\frac{AN}{NC}\) (định lí Thalès)
\(\Rightarrow \frac{6,5}{x}=\frac{4}{2}=2\)
Vậy x = 6,5 : 2 = 3,25
b) Ta có FE ⊥ PH, QH ⊥ PH nên EF // HQ
Xét tam giác PHQ có EF // HQ:
⇒ \(\frac{PE}{PH}=\frac{PF}{PQ}\) (định lí Thalès)
\(\Rightarrow \frac{4}{y}=\frac{5}{5+3,5}\Rightarrow y=6,8\)
Hoạt động 4 trang 79 Toán 8 tập 1 Kết nối
Cho ∆ ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 4 cm, AC' = 6 cm (H.4.7).
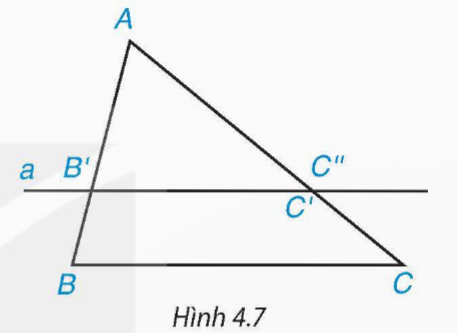
• So sánh các tỉ số \(\frac{AB'}{AB}\) và \(\frac{AC'}{AC}\)
• Vẽ đường thẳng a đi qua B' và song song với BC, đường thẳng a cắt AC tại điểm C''. Tính độ dài đoạn thẳng AC''.
• Nhận xét gì về hai điểm C', C'' và hai đường thẳng B'C', BC?
Hướng dẫn giải:
Ta có: \(\frac{AB'}{AB}=\frac{4}{6}=\frac{2}{3}\)
\(\frac{AC'}{AC}=\frac{6}{9}=\frac{2}{3}\)
Do đó \(\frac{AB'}{AB}=\frac{AC'}{AC}\)
Xét tam giác ABC có B'C'' // BC:
⇒ \(\frac{AB'}{AB}=\frac{AC''}{AC}\) (theo định lí Thalès)
\(\Rightarrow \frac{4}{6}=\frac{AC''}{9}\Rightarrow AC''=6\)
Nhận xét: C' và C" trùng nhau nên BC' // BC.
-----------------------------------------------
Lời giải Toán 8 trang 79 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức bài 15: Định lí Thalès trong tam giác, được VnDoc biên soạn và đăng tải!
