Giải Toán 8 trang 90 tập 2 Kết nối tri thức
Giải Toán 8 trang 90 Tập 2
Giải Toán 8 trang 90 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 90.
Bài 9.5 trang 90 Toán 8 tập 2 Kết nối
Khẳng định nào sau đây chứng tỏ rằng hai tam giác đồng dạng?
a) Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
b) Hai cạnh của tam giá này tỉ lệ với hai cạnh của tam giác kia và có một cặp góc bằng nhau.
c) Hai góc của tam giác này bằng hai góc của tam giác kia.
d) Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.
Hướng dẫn giải:
Các khẳng định chứng tỏ hai tam giác đồng dạng là: a) và c).
Bài 9.6 trang 90 Toán 8 tập 2 Kết nối
Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?
a) 6 cm, 12 cm, 15 cm
b) 8 cm, 16 cm, 20 cm
c) 6 cm, 9 cm, 18 cm
d) 8 cm, 10 cm, 15 cm
Hướng dẫn giải:
Ta có 6 + 12 + 15 = 33 cm và 
\(\frac{4}{6}=\frac{8}{12}=\frac{10}{15}=\frac{2}{3}\) nên bộ ba trong câu a) thỏa mãn yêu cầu.
Các phương án khác không có tổng bằng 33 cm hoặc không có tỉ lệ tương ứng với (4 : 8 : 10) nên không thỏa mãn.
Bài 9.7 trang 90 Toán 8 tập 2 Kết nối
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng Δ A'B'C' ∽ Δ ABC.
Chứng minh rằng \(\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}\).
Hướng dẫn giải:
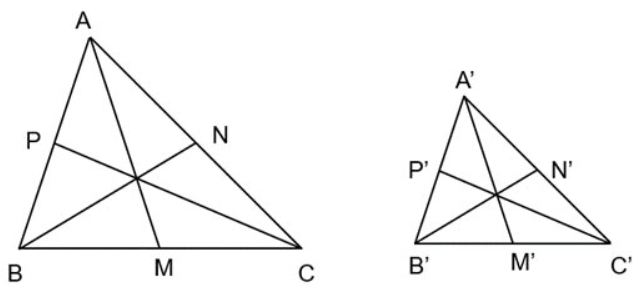
Vì Δ A'B'C' ∽ Δ ABC nên \(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\) (1)
⇒ \(\widehat{A'B'C'} =\widehat{ABC},\ \widehat{B'C'A'}=\widehat{BCA}, \ \widehat{C'A'B'}=\widehat{CAB}\)
Hai tam giác A'B'M' và ABM có:
\(\frac{B'M'}{BM}=\frac{\frac{B'C'}{2}}{\frac{BC}{2}}=\frac{B'C'}{BC}=\frac{B'A'}{BA}\)
\(\widehat{A'B'M'} =\widehat{A'B'C'}=\widehat{ABC}=\widehat{ABM}\)
⇒ Δ A'B'M' ∽ Δ ABM (c.g.c).
⇒ \(\frac{B'M'}{BM}=\frac{B'A'}{BA}\) (2)
Tương tự: Δ A'B'N' ∽ Δ ABN và \(\frac{B'N'}{BN}=\frac{B'C'}{BC}\) (3);
Δ C'A'P' ∽ Δ CAP và \(\frac{C'P'}{CP}=\frac{A'C'}{AC}\) (4).
Từ (1), (2), (3) và (4) suy ra \(\frac{A'M'}{AM}=\frac{B'N'}{BN}=\frac{C'P'}{CP}\).
Bài 9.8 trang 90 Toán 8 tập 2 Kết nối
Cho tam giác ABC có AB = 12 cm , AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10 cm, AN = 8 cm. Chứng minh rằng Δ ABC ∽ Δ ANM
Hướng dẫn giải:
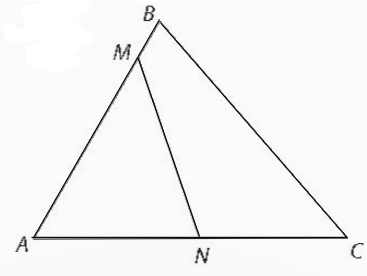
Xét tam giác ABC và tam giác ANM, có
\(\frac{AB}{AN}=\frac{AC}{AM} = \frac{3}{ 2}\)
Góc A chung
⇒ Δ ABC ∽ Δ ANM (c . g . c)
Bài 9.9 trang 90 Toán 8 tập 2 Kết nối
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\)
a) Chứng minh rằng Δ ABN ∽ Δ ACM
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB . IN = IC . IM
Hướng dẫn giải:
Đang cập nhật...
Bài 9.10 trang 90 Toán 8 tập 2 Kết nối
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
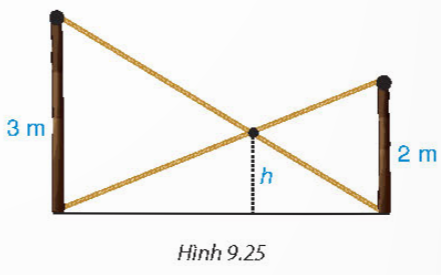
Hướng dẫn giải:
Đang cập nhật...
-----------------------------------------------
Lời giải Toán 8 trang 90 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 34: Ba trường hợp đồng dạng của hai tam giác, được VnDoc biên soạn và đăng tải!
