Giải Toán 8 trang 87 tập 2 Kết nối tri thức
Giải Toán 8 trang 87 Tập 2
Giải Toán 8 trang 87 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 87.
Luyện tập 2 trang 87 Toán 8 tập 2 Kết nối
Cho Δ A'B'C' ∽ Δ ABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho 
\(\frac{MC}{MB}=\frac{M'C'}{MB}\). Chứng minh rằng Δ A'B'M' ∽ Δ ABM.
Hướng dẫn giải:
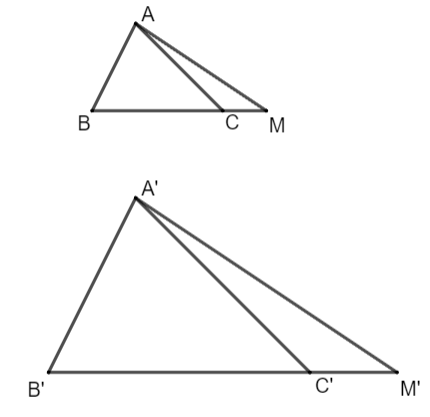
Vì Δ A'B'C' ∽ Δ ABC nên \(\widehat{A'B'C'}=\widehat{ABC}\) và \(\frac{A'B'}{AB}=\frac{B'C'}{BC}\).
⇒ \(\frac{M'B'}{MB}=\frac{M'C'}{MC}=\frac{M'B'-M'C'}{MB-MC}=\frac{B'C'}{BC}\)
Hai tam giác A'B'M' và ABM có \(\frac{A'B'}{AB}=\frac{B'M'}{BM}\) và \(\widehat{A'B'M'}=\widehat{ABM}\)
Vậy Δ A'B'M' ∽ Δ ABM (c.g.c).
-----------------------------------------------
Lời giải Toán 8 trang 87 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 34: Ba trường hợp đồng dạng của hai tam giác, được VnDoc biên soạn và đăng tải!
