Toán 8 Cánh diều bài 2: Các phép tính với đa thức nhiều biến

Giải Toán 8 Cánh diều trang 11, 12, 13, 14

Giải Toán 8 Cánh diều bài 2: Các phép tính với đa thức nhiều biến hướng dẫn giải bài tập trong sách giáo khoa Toán 8 Cánh diều, giúp các em nắm vững kiến thức được học và nâng cao kỹ năng giải Toán 8. Mời các em cùng tham khảo chi tiết sau đây.

Bài 2: Các phép tính với đa thức nhiều biến

Khởi động trang 11 Toán 8 Tập 1:
I. Cộng hai đa thức
- Hoạt động 1 trang 11 sgk Toán 8 tập 1 CD:
- Luyện tập 1 trang 11 sgk Toán 8 tập 1 CD:
II. Trừ hai đa thức
- Hoạt động 2 trang 12 sgk Toán 8 tập 1 CD:
- Luyện tập 2 trang 13 sgk Toán 8 tập 1 CD:
III. Nhân hai đa thức
- Hoạt động 3 trang 13 sgk Toán 8 tập 1 CD:
- Luyện tập 3 trang 13 sgk Toán 8 tập 1 CD:
2. Nhân đơn thức với đa thức
- Hoạt động 4 trang 13 sgk Toán 8 tập 1 CD:
- Luyện tập 4 trang 14 sgk Toán 8 tập 1 CD:
3. Nhân hai đa thức
- Hoạt động 5 trang 14 sgk Toán 8 tập 1 CD:
- Luyện tập 5 trang 14 sgk Toán 8 tập 1 CD:
IV. Chia đa thức cho đơn thức
- Hoạt động 6 trang 15 sgk Toán 8 tập 1 CD:
- Luyện tập 6 trang 15 sgk Toán 8 tập 1 CD:
2. Phép chia hết một đa thức cho một đơn thức.
- Hoạt động 7 trang 16 sgk Toán 8 tập 1 CD:
- Luyện tập 7 trang 16 sgk Toán 8 tập 1 CD:
V. Giải bài tập trang 16 sgk Toán 8 tập 1 CD:
Trắc nghiệm Toán 8 bài 2 Cánh diều

Khởi động trang 11 Toán 8 Tập 1:

Ở lớp 7, ta đã học cách thực hiện phép cộng, phép trừ, phép nhân, phép chia các đa thức một biến.

Các phép tính với đa thức (nhiều biến) được thực hiện như thế nào?

Hướng dẫn giải

Sau bài học này chúng ta giải quyết bài toán này như sau:

Các phép tính với đa thức (nhiều biến) được thực hiện tương tự các phép tính với đa thức một biến.

I. Cộng hai đa thức

Hoạt động 1 trang 11 sgk Toán 8 tập 1 CD:

Cho hai đa thức: $P = x^{2} + 2xy + y^{2}; Q = x^{2} - 2xy + y^{2}$ $P = x^{2} + 2xy + y^{2}; Q = x^{2} - 2xy + y^{2}$

a) Viết tổng P + Q theo hàng ngang.

b) Nhóm các đơn thức đồng dạng với nhau.

c) Tính tổng P + Q bằng cách thực hiện phép tính trong từng nhóm.

Hướng dẫn giải

a) Viết tổng P + Q theo hàng ngang:

$P+Q = (x^{2} + 2xy + y^{2} )+ (x^{2} - 2xy + y^{2})$ $P+Q = (x^{2} + 2xy + y^{2} )+ (x^{2} - 2xy + y^{2})$

b) Nhóm các đơn thức đồng dạng với nhau:

$P+Q = (1+1)x^{2} + (2-2)xy + (1+1)y^{2}$ $P+Q = (1+1)x^{2} + (2-2)xy + (1+1)y^{2}$

c) Tính tổng P + Q bằng cách thực hiện phép tính trong từng nhóm:

$P+Q = 2x^{2} + 2y^{2}$ $P+Q = 2x^{2} + 2y^{2}$

Luyện tập 1 trang 11 sgk Toán 8 tập 1 CD:

Tính tổng của hai đa thức: $M= x^{3}+ y^{3}; N= x^{3}- y^{3}$ $M= x^{3}+ y^{3}; N= x^{3}- y^{3}$

Hướng dẫn giải

Tổng: $M + N = (x^{3}+ y^{3}) + (x^{3}- y^{3})$ $M + N = (x^{3}+ y^{3}) + (x^{3}- y^{3})$

$= x^{3}+y^{3} + x^{3}- y^{3} = 2x^{3}$ $= x^{3}+y^{3} + x^{3}- y^{3} = 2x^{3}$

II. Trừ hai đa thức

Hoạt động 2 trang 12 sgk Toán 8 tập 1 CD:

Cho hai đa thức: $P = x^{2} + 2xy + y^{2}; Q = x^{2} - 2xy + y^{2}$ $P = x^{2} + 2xy + y^{2}; Q = x^{2} - 2xy + y^{2}$

a) Viết hiệu P - Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc.

b) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức đồng dạng với nhau.

c) Tính hiệu P - Q bằng cách thực hiện phép tính trong từng nhóm.

Hướng dẫn giải

a) Viết hiệu P - Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc:

$P - Q =x^{2} + 2xy + y^{2} - (x^{2} - 2xy + y^{2})$ $P - Q =x^{2} + 2xy + y^{2} - (x^{2} - 2xy + y^{2})$

b) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức đồng dạng với nhau:

$P - Q = x^{2} + 2xy + y^{2} - x^{2} + 2xy - y^{2}$ $P - Q = x^{2} + 2xy + y^{2} - x^{2} + 2xy - y^{2}$

$= (x^{2} -x^{2} )+(2xy +2xy )+ (y^{2}-y^{2})$ $= (x^{2} -x^{2} )+(2xy +2xy )+ (y^{2}-y^{2})$

c) Tính hiệu P - Q bằng cách thực hiện phép tính trong từng nhóm: P - Q = 4xy

Luyện tập 2 trang 13 sgk Toán 8 tập 1 CD:

Với 3 đa thức A,B,C trong ví dụ 3, hãy tính:

a. B-C

b. (B-C)+A

Với: $A= x^{2} - 2xy + y^{2}; B= 2x^{2} - y^{2}; C= x^{2} - 3xy$ $A= x^{2} - 2xy + y^{2}; B= 2x^{2} - y^{2}; C= x^{2} - 3xy$

Hướng dẫn giải

$a. B-C = (2x^{2} - y^{2}) - (x^{2} - 3xy)$ $a. B-C = (2x^{2} - y^{2}) - (x^{2} - 3xy)$

$= 2x^{2} - y^{2} - x^{2} + 3xy$ $= 2x^{2} - y^{2} - x^{2} + 3xy$

$= (2x^{2}-x^{2}) - y^{2}+ 3xy = x^{2}+3xy-y^{2}$ $= (2x^{2}-x^{2}) - y^{2}+ 3xy = x^{2}+3xy-y^{2}$

$b. (B-C)+A = x^{2}+3xy-y^{2}+x^{2} - 2xy + y^{2}$ $b. (B-C)+A = x^{2}+3xy-y^{2}+x^{2} - 2xy + y^{2}$

$= (x^{2}+x^{2}) + (3xy-2xy) - (y^{2}-y^{2}) = 2x^{2}+xy$ $= (x^{2}+x^{2}) + (3xy-2xy) - (y^{2}-y^{2}) = 2x^{2}+xy$

III. Nhân hai đa thức

Hoạt động 3 trang 13 sgk Toán 8 tập 1 CD:

a. Tính tích: $3x^{2}.8x^{4}$ $3x^{2}.8x^{4}$

b. Nêu quy tắc nhân hai đơn thức một biến.

Hướng dẫn giải

a. Tính tích:

$3x^{2}.8x^{4} = 3.8.x^{2+4} = 24x^{6}$ $3x^{2}.8x^{4} = 3.8.x^{2+4} = 24x^{6}$

b. Nêu quy tắc nhân hai đơn thức một biến:

- Nhân các hệ số với nhau, và nhân các phần biến với nhau.

- Thu gọn đơn thức thu được ở tích.

Luyện tập 3 trang 13 sgk Toán 8 tập 1 CD:

Tính tích của hai đơn thức: $x^{3}y^{7}; -2x^{5}y^{3}$ $x^{3}y^{7}; -2x^{5}y^{3}$

Hướng dẫn giải

$(x^{3}y^{7}). (-2x^{5}y^{3})$ $(x^{3}y^{7}). (-2x^{5}y^{3})$

$= (1.(-2)). (x^{3}.x^{5}). (y^{7}.y^{3}) = (-2). x^{8}y^{10}$ $= (1.(-2)). (x^{3}.x^{5}). (y^{7}.y^{3}) = (-2). x^{8}y^{10}$

2. Nhân đơn thức với đa thức

Hoạt động 4 trang 13 sgk Toán 8 tập 1 CD:

a. Tính tích: $x^{3}(x^{2}-x+1)$ $x^{3}(x^{2}-x+1)$

b. Nêu quy tắc nhân đơn thức với đa thức trong trường hợp một biến.

Hướng dẫn giải

a. Tính tích:

$x^{3}(x^{2}-x+1)= x^{3}.x^{2} - x^{3}.x + x^{3}.1$ $x^{3}(x^{2}-x+1)= x^{3}.x^{2} - x^{3}.x + x^{3}.1$

$= x^{3+2} - x^{3+1} + x^{3} = x^{5} - x^{4} + x^{3}$ $= x^{3+2} - x^{3+1} + x^{3} = x^{5} - x^{4} + x^{3}$

b. Quy tắc nhân đơn thức với đa thức trong trường hợp một biến: ta nhân đơn thức đó với từng đa thức rồi cộng các kết quả với nhau.

Luyện tập 4 trang 14 sgk Toán 8 tập 1 CD:

Tính tích: $(-\frac{1}{2}xy)(8x^{2}-5xy+2y^{2})$ $(-\frac{1}{2}xy)(8x^{2}-5xy+2y^{2})$

Hướng dẫn giải

Tính tích:

$(-\frac{1}{2}xy)(8x^{2}-5xy+2y^{2})$ $(-\frac{1}{2}xy)(8x^{2}-5xy+2y^{2})$

$= (-\frac{1}{2}xy.8x^{2}) - (-\frac{1}{2}xy).5xy + (-\frac{1}{2}xy).2y^{2}$ $= (-\frac{1}{2}xy.8x^{2}) - (-\frac{1}{2}xy).5xy + (-\frac{1}{2}xy).2y^{2}$

$= (-\frac{1}{2}.8)xy.x^{2}+(-\frac{1}{2}.5)xy.xy+(-\frac{1}{2}).2xy.y^{2}$ $= (-\frac{1}{2}.8)xy.x^{2}+(-\frac{1}{2}.5)xy.xy+(-\frac{1}{2}).2xy.y^{2}$

$= -4x^{3}+\frac{5}{2}x^{2}y^{2}-xy^{3}$ $= -4x^{3}+\frac{5}{2}x^{2}y^{2}-xy^{3}$

3. Nhân hai đa thức

Hoạt động 5 trang 14 sgk Toán 8 tập 1 CD:

a. Tính tích:

b. Nêu quy tắc nhân hai đa thức trong trường hợp một biến.

Hướng dẫn giải

a. Tính tích:

$(x+1)(x^{2}-x+1)$ $(x+1)(x^{2}-x+1)$

$= x.x^{2}+x.(-x)+x.1+1.x^{2}+1.(-x)+1.1$ $= x.x^{2}+x.(-x)+x.1+1.x^{2}+1.(-x)+1.1$

$=x^{2+1}-x^{2}+x+x^{2}-x+1=x^{3}+1$ $=x^{2+1}-x^{2}+x+x^{2}-x+1=x^{3}+1$

b. Nêu quy tắc nhân hai đa thức trong trường hợp một biến: Ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các kết quả lại với nhau.

Luyện tập 5 trang 14 sgk Toán 8 tập 1 CD:

Tính (x-y)(x-y)

Hướng dẫn giải

Tính:

$(x-y)(x-y) = x.x-x.y-y.x+y.y = x^{2}-2xy+y^{2}$ $(x-y)(x-y) = x.x-x.y-y.x+y.y = x^{2}-2xy+y^{2}$

IV. Chia đa thức cho đơn thức

Hoạt động 6 trang 15 sgk Toán 8 tập 1 CD:

Tính tích: $9x^{5}y^{4}.2x^{4}y^{2}$ $9x^{5}y^{4}.2x^{4}y^{2}$

Hướng dẫn giải

Tính tích:

$9x^{5}y^{4}.2x^{4}y^{2}$ $9x^{5}y^{4}.2x^{4}y^{2}$

$= (9.2).(x^{5}.x^{4}).(y^{4}.y^{2}) = 18.x^{5+4}. y^{4+2}$ $= (9.2).(x^{5}.x^{4}).(y^{4}.y^{2}) = 18.x^{5+4}. y^{4+2}$

$= 18x^{9}y^{6}$ $= 18x^{9}y^{6}$

Luyện tập 6 trang 15 sgk Toán 8 tập 1 CD:

Cho $P = (21x^{4}y^{5}):(7x^{3}y^{3})$ $P = (21x^{4}y^{5}):(7x^{3}y^{3})$. Tính giá trị của biểu thức P tại x= -0,5; y= -2

Hướng dẫn giải

Ta có:

$P = (21x^{4}y^{5}):(7x^{3}y^{3})$ $P = (21x^{4}y^{5}):(7x^{3}y^{3})$

$= (21:7).(x^{4}:x^{3}).(y^{5}:y^{3})$ $= (21:7).(x^{4}:x^{3}).(y^{5}:y^{3})$

$= 3.x^{4-3}.y^{5-3}$ = 3.x.y^{2}.$ $= 3.x^{4-3}.y^{5-3}$ = 3.x.y^{2}.$

Tại x= -0,5; y= -2, giá trị của $P = 3.x.y^{2} = 3.(-0,5).(-2)^{2}$ $P = 3.x.y^{2} = 3.(-0,5).(-2)^{2}$ = -1,5.4=-6

2. Phép chia hết một đa thức cho một đơn thức.

Hoạt động 7 trang 16 sgk Toán 8 tập 1 CD:

Tính tích (3xy).(x+y)

Hướng dẫn giải

Tính tích:

$(3xy).(x+y) =3xy.x+3xy.y = 3x^{2}y+3xy^{2}$ $(3xy).(x+y) =3xy.x+3xy.y = 3x^{2}y+3xy^{2}$

Luyện tập 7 trang 16 sgk Toán 8 tập 1 CD:

Tìm thương trong phép chia đa thức: $12x^{3}y^{3}- 6x^{4}y^{3}+21x^{3}y^{4}$ $12x^{3}y^{3}- 6x^{4}y^{3}+21x^{3}y^{4}$cho đơn thức $3x^{3}y^{3}$ $3x^{3}y^{3}$

Hướng dẫn giải

Tìm thương trong phép chia đa thức:

$(12x^{3}y^{3}- 6x^{4}y^{3}+21x^{3}y^{4}): (3x^{3}y^{3})$ $(12x^{3}y^{3}- 6x^{4}y^{3}+21x^{3}y^{4}): (3x^{3}y^{3})$

$= (12x^{3}y^{3}: 3x^{3}y^{3}) - (6x^{4}y^{3}:3x^{3}y^{3})+(21x^{3}y^{4}:3x^{3}y^{3})$ $= (12x^{3}y^{3}: 3x^{3}y^{3}) - (6x^{4}y^{3}:3x^{3}y^{3})+(21x^{3}y^{4}:3x^{3}y^{3})$

$= (12:3)(x^{3}y^{3}: x^{3}y^{3}) - (6:3)(x^{4}y^{3}:3x^{3}y^{3}) + (21:3).(x^{3}y^{4}:x^{3}y^{3})$ $= (12:3)(x^{3}y^{3}: x^{3}y^{3}) - (6:3)(x^{4}y^{3}:3x^{3}y^{3}) + (21:3).(x^{3}y^{4}:x^{3}y^{3})$

$= 4.1-2x+7y=4-2x+7y$

V. Giải bài tập trang 16 sgk Toán 8 tập 1 CD:

Bài tập 1 trang 16 sgk Toán 8 tập 1 CD:

Thực hiện phép tính:

$a. (-xy)(-2x^{2}y+3xy-7x)$ $a. (-xy)(-2x^{2}y+3xy-7x)$

$b. (\frac{1}{6}x^{2}y^{2})(-0,3x^{2}y-0,4xy+1)$ $b. (\frac{1}{6}x^{2}y^{2})(-0,3x^{2}y-0,4xy+1)$

$c. (x+y)(x^{2}+2xy+y^{2})$ $c. (x+y)(x^{2}+2xy+y^{2})$

$d. (x-y)(x^{2}-2xy+y^{2})$ $d. (x-y)(x^{2}-2xy+y^{2})$

Hướng dẫn giải

$a. (-xy)(-2x^{2}y+3xy-7x)$ $a. (-xy)(-2x^{2}y+3xy-7x)$

$= (-1)(-2).(xy.x^{2}y+(-1).3.xy.xy+(-1)(-7).xy.x$ $= (-1)(-2).(xy.x^{2}y+(-1).3.xy.xy+(-1)(-7).xy.x$

$= 2.x^{2+1}y^{2}-3.x^{2}y^{2}+7.x^{2}y$ $= 2.x^{2+1}y^{2}-3.x^{2}y^{2}+7.x^{2}y$

$= 2x^{3}y^{2}-3.x^{2}y^{2}+7.x^{2}y$ $= 2x^{3}y^{2}-3.x^{2}y^{2}+7.x^{2}y$

$b. (\frac{1}{6}x^{2}y^{2})(-0,3x^{2}y-0,4xy+1)$ $b. (\frac{1}{6}x^{2}y^{2})(-0,3x^{2}y-0,4xy+1)$

$= \frac{1}{6}.(-0,3).x^{2}.x^{2}.y^{2}.y-(\frac{1}{6}.0,4).x^{2}.x.y^{2}.y+\frac{1}{6}.x^{2}.y^{2}$ $= \frac{1}{6}.(-0,3).x^{2}.x^{2}.y^{2}.y-(\frac{1}{6}.0,4).x^{2}.x.y^{2}.y+\frac{1}{6}.x^{2}.y^{2}$

$= (-0,05).x^{4}.y^{3}-\frac{0,4}{6}.x^{3}.y^{3}+\frac{1}{6}.x^{2}.y^{2}$ $= (-0,05).x^{4}.y^{3}-\frac{0,4}{6}.x^{3}.y^{3}+\frac{1}{6}.x^{2}.y^{2}$

$c. (x+y)(x^{2}+2xy+y^{2})$ $c. (x+y)(x^{2}+2xy+y^{2})$

$= x.x^{2}+1.2.x.x.y+x.y^{2}+y.x^{2}+1.2.x.y.y+y.y^{2}$ $= x.x^{2}+1.2.x.x.y+x.y^{2}+y.x^{2}+1.2.x.y.y+y.y^{2}$

$= x^{3}+2.x^{2}.y+x.y^{2}+y.x^{2}+2.x.y^{2}+y^{3}$ $= x^{3}+2.x^{2}.y+x.y^{2}+y.x^{2}+2.x.y^{2}+y^{3}$

$= x^{3}+3.x^{2}.y+3x.y^{2}+y^{3}.$ $= x^{3}+3.x^{2}.y+3x.y^{2}+y^{3}.$

$d. (x-y)(x^{2}-2xy+y^{2})$ $d. (x-y)(x^{2}-2xy+y^{2})$

$=x.x^{2}-1.2.x.x.y+x.y^{2}-y.x^{2}+(-1)(-2).y.x.y-y.y^{2}$ $=x.x^{2}-1.2.x.x.y+x.y^{2}-y.x^{2}+(-1)(-2).y.x.y-y.y^{2}$

$= x^{3}-2.x^{2}.y+x.y^{2}-y.x^{2}+2.x.y^{2}-y^{3}$ $= x^{3}-2.x^{2}.y+x.y^{2}-y.x^{2}+2.x.y^{2}-y^{3}$

$= x^{3}-3.x^{2}.y+3x.y^{2}-y^{3}$ $= x^{3}-3.x^{2}.y+3x.y^{2}-y^{3}$

Bài tập 2 trang 16 sgk Toán 8 tập 1 CD:

Thực hiện phép tính:

$a. (39x^{5}y^{7}):(13x^{2})$ $a. (39x^{5}y^{7}):(13x^{2})$

$b. (x^{2}y^{2}+\frac{1}{6}x^{3}y^{2}-x^{5}y^{4}):(\frac{1}{2}xy^{2})$ $b. (x^{2}y^{2}+\frac{1}{6}x^{3}y^{2}-x^{5}y^{4}):(\frac{1}{2}xy^{2})$

Hướng dẫn giải

Thực hiện phép tính:

$a. (39x^{5}y^{7}):(13x^{2}) = (39:3)(x^{5}:x^{2})(y^{7}:y)$ $a. (39x^{5}y^{7}):(13x^{2}) = (39:3)(x^{5}:x^{2})(y^{7}:y)$

$= 13.x^{5-2}.y^{7-1} = 13.x^{3}.y^{6}$ $= 13.x^{5-2}.y^{7-1} = 13.x^{3}.y^{6}$

$b. (x^{2}y^{2}+\frac{1}{6}x^{3}y^{2}-x^{5}y^{4}):(\frac{1}{2}xy^{2})$ $b. (x^{2}y^{2}+\frac{1}{6}x^{3}y^{2}-x^{5}y^{4}):(\frac{1}{2}xy^{2})$

$= (x^{2}y^{2} : \frac{1}{2}xy^{2}) + (\frac{1}{6}x^{3}y^{2} : \frac{1}{2}xy^{2}) - (x^{5}y^{4}:\frac{1}{2}xy^{2})$ $= (x^{2}y^{2} : \frac{1}{2}xy^{2}) + (\frac{1}{6}x^{3}y^{2} : \frac{1}{2}xy^{2}) - (x^{5}y^{4}:\frac{1}{2}xy^{2})$

$= (1:\frac{1}{2})(x^{2}:x)(y^{2}:y^{2})+(\frac{1}{6}:\frac{1}{2})(x^{3}:x)(y^{2}:y^{2})-(1:\frac{1}{2})(x^{5}:x)(y^{4}:y^{2})$ $= (1:\frac{1}{2})(x^{2}:x)(y^{2}:y^{2})+(\frac{1}{6}:\frac{1}{2})(x^{3}:x)(y^{2}:y^{2})-(1:\frac{1}{2})(x^{5}:x)(y^{4}:y^{2})$

$= 2(x^{2-1}y^{2-2})+(\frac{1}{3}x^{3-1}y^{2-2})-(2x^{5-1}y^{4-2})$ $= 2(x^{2-1}y^{2-2})+(\frac{1}{3}x^{3-1}y^{2-2})-(2x^{5-1}y^{4-2})$

$= 2x^{1}+\frac{1}{3}x^{2}-2x^{4}y^{2}$ $= 2x^{1}+\frac{1}{3}x^{2}-2x^{4}y^{2}$

Bài tập 3 trang 17 sgk Toán 8 tập 1 CD:

Rút gọn biểu thức.

$a. (x-y)(x^{2}+xy+y^{2})$ $a. (x-y)(x^{2}+xy+y^{2})$

$b. (x+y)(x^{2}-xy+y^{2})$ $b. (x+y)(x^{2}-xy+y^{2})$

$c. (4x-1)(6y+1)-3x(8y+\frac{4}{3})$ $c. (4x-1)(6y+1)-3x(8y+\frac{4}{3})$

$d. (x+y)(x-y)+ (xy^{4}-x^{3}y^{2}):(xy^{2})$ $d. (x+y)(x-y)+ (xy^{4}-x^{3}y^{2}):(xy^{2})$

Hướng dẫn giải

Rút gọn biểu thức.

$a. (x-y)(x^{2}+xy+y^{2})$ $a. (x-y)(x^{2}+xy+y^{2})$

$= x.x^{2}+x.x.y+x.y^{2}-y.x^{2}-x.y^{2}-y^{3}$ $= x.x^{2}+x.x.y+x.y^{2}-y.x^{2}-x.y^{2}-y^{3}$

$= x^{3}+x^{2}.y+x.y^{2}-y.x^{2}-x.y^{2}-y^{3} = x^{3}-y^{3}$ $= x^{3}+x^{2}.y+x.y^{2}-y.x^{2}-x.y^{2}-y^{3} = x^{3}-y^{3}$

$b. (x+y)(x^{2}-xy+y^{2})$ $b. (x+y)(x^{2}-xy+y^{2})$

$= x.x^{2}-x.xy+x.y^{2}+y.x^{2}-y.xy+y.y^{2}$ $= x.x^{2}-x.xy+x.y^{2}+y.x^{2}-y.xy+y.y^{2}$

$= x^{2+1}-x^{2}y+x.y^{2}+y.x^{2}-xy^{2}+y^{2+1} = x^{3}+y^{3}$ $= x^{2+1}-x^{2}y+x.y^{2}+y.x^{2}-xy^{2}+y^{2+1} = x^{3}+y^{3}$

$c. (4x-1)(6y+1)-3x(8y+\frac{4}{3})$ $c. (4x-1)(6y+1)-3x(8y+\frac{4}{3})$

$=(4.6.x.y+4x-1)-3.8.x.y-3.(\frac{4}{3})x$ $=(4.6.x.y+4x-1)-3.8.x.y-3.(\frac{4}{3})x$

$= 24xy+4x-1-24xy-4x = -1$

$d. (x+y)(x-y)+ (xy^{4}-x^{3}y^{2}):(xy^{2})$ $d. (x+y)(x-y)+ (xy^{4}-x^{3}y^{2}):(xy^{2})$

$= x.x-x.y+y.x-y.y+(x:x)(y^{4}:y^{2})-(x^{3}:x)(y^{2}:y^{2})$ $= x.x-x.y+y.x-y.y+(x:x)(y^{4}:y^{2})-(x^{3}:x)(y^{2}:y^{2})$

$= x^{2}-xy+y.x-y^{2}+1.y^{4-2}-x^{3-1}.1$ $= x^{2}-xy+y.x-y^{2}+1.y^{4-2}-x^{3-1}.1$

$= x^{2}-xy+y.x-y^{2}+y^{2}-x^{2} = 0$ $= x^{2}-xy+y.x-y^{2}+y^{2}-x^{2} = 0$

Bài tập 4 trang 17 sgk Toán 8 tập 1 CD:

a. Rút gọn rồi tính giá trị của biểu thức.

$P = (5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$ $P = (5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$, khi x=1,2 và x+y=6,2

b. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

$(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$ $(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$

Hướng dẫn giải

a. Rút gọn rồi tính giá trị của biểu thức.

$P = (5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$ $P = (5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$

$= 5x^{2}-2xy+y^{2}-x^{2}-y^{2}-4x^{2}+5xy-1$ $= 5x^{2}-2xy+y^{2}-x^{2}-y^{2}-4x^{2}+5xy-1$

$= (5x^{2}-x^{2}-4x^{2})-(2xy-5xy)+(y^{2}-y^{2})-1$ $= (5x^{2}-x^{2}-4x^{2})-(2xy-5xy)+(y^{2}-y^{2})-1$

$= 0+3xy-1 = 3xy$

Khi x=1,2 và x+y=6,2 =>y = 6,2-1,2=5.

Vậy giá trị của P = 3.1,2.5=18

b. Ta có:

$(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$ $(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$

$= x^{2}.2x+x^{2}.3-5.2.x.x-5x.3+4.2x+4.3-(2x^{2}.x-2.(-3).x^{2}-x.x+3x-10x+10.3)$ $= x^{2}.2x+x^{2}.3-5.2.x.x-5x.3+4.2x+4.3-(2x^{2}.x-2.(-3).x^{2}-x.x+3x-10x+10.3)$

$= 2x^{2+1}+3x^{2}-10x^{2}-15x+8x+12-2x^{2+1}+6.x^{2}+x^{2}-3x+10x-30$ $= 2x^{2+1}+3x^{2}-10x^{2}-15x+8x+12-2x^{2+1}+6.x^{2}+x^{2}-3x+10x-30$

$= (2x^{3}-2x^{3})+(3x^{2}+6.x^{2}+x^{2}-10x^{2})-(15x-8x+3x-10x)-30+12$ $= (2x^{3}-2x^{3})+(3x^{2}+6.x^{2}+x^{2}-10x^{2})-(15x-8x+3x-10x)-30+12$

$= -18.$

Như vậy giá trị của biểu thức luôn là 18 và không phụ thuộc vào giá trị của biến x

Bài tập 5 trang 17 sgk Toán 8 tập 1 CD:

a. Chứng minh rằng biểu thức $P=5x(2-x)-(x+1)(x+9)$ luôn nhận giá trị âm với mọi giá trị của biến x.

b. Chứng minh rằng biểu thức $Q = 3x^{2}+x(x-4y)-2x(6-2y)+12x+1$ $Q = 3x^{2}+x(x-4y)-2x(6-2y)+12x+1$ luôn nhận giá trị dương với mọi giá trị của biến x và y.

Hướng dẫn giải

a. Ta có:

$P = 5x(2-x)-(x+1)(x+9)$

$= 5.2.x - 5.x.x - (x.x+x.9+1.x+1.9)$

$= 10x-5x^{2}-x^{2}-9x-x-9 = -6x^{2}-9$ $= 10x-5x^{2}-x^{2}-9x-x-9 = -6x^{2}-9$

Vì $x^{2}\geq 0 =>-6x^{2} \leq 0 =>-6x^{2}-9\leq 0$ $x^{2}\geq 0 =>-6x^{2} \leq 0 =>-6x^{2}-9\leq 0$

Vậy P luôn nhận giá trị âm với mọi giá trị của biến x.

b. Ta có:

$Q = 3x^{2}+x(x-4y)-2x(6-2y)+12x+1$ $Q = 3x^{2}+x(x-4y)-2x(6-2y)+12x+1$

$= 3x^{2}+x.x-4.x.y-2.6.x+2.2.x.y+12x+1$ $= 3x^{2}+x.x-4.x.y-2.6.x+2.2.x.y+12x+1$

$= 3x^{2}+x^{2}-4xy-12x+4xy+12x+1 = 4x^{2}+1$ $= 3x^{2}+x^{2}-4xy-12x+4xy+12x+1 = 4x^{2}+1$

Vì $x^{2}\geq 0 =>4x^{2}\geq 0 =>4x^{2}+1\geq 1$ $x^{2}\geq 0 =>4x^{2}\geq 0 =>4x^{2}+1\geq 1$

Vậy Q luôn nhận giá trị dương với mọi giá trị của biến x và y.

Bài tập 6 trang 17 sgk Toán 8 tập 1 CD:

Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lân lượt là 6 (cm), 8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ dài cạnh góc vuông 8 (cm) thêm y (cm) (Hình 3). Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y.

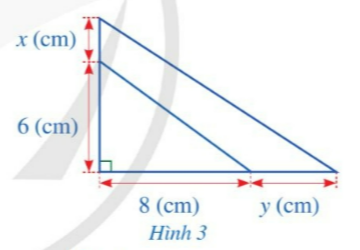
Giải bài tập 6 trang 17 sgk Toán 8 tập 1 CD

Hướng dẫn giải

Diện tích của miếng bìa theo dự định lúc đầu là: $S_{1} = \frac{1}{2}.6.8 = 24 (cm^{2}).$ $S_{1} = \frac{1}{2}.6.8 = 24 (cm^{2}).$

Diện tích của miếng bìa sau khi tăng thêm các cạnh góc vuông là:

$S_{2} = \frac{1}{2}.(6+x).(8+y)$ $S_{2} = \frac{1}{2}.(6+x).(8+y)$

$= \frac{1}{2}.6.8+\frac{1}{2}.6.y+\frac{1}{2}.8.x+\frac{1}{2}.x.y$ $= \frac{1}{2}.6.8+\frac{1}{2}.6.y+\frac{1}{2}.8.x+\frac{1}{2}.x.y$

$= 24+3y+4x+\frac{1}{2}xy (cm^{2}).$ $= 24+3y+4x+\frac{1}{2}xy (cm^{2}).$

Vậy phần diện tích tăng thêm sẽ là: $3y+4x+\frac{1}{2}xy (cm^{2}).$ $3y+4x+\frac{1}{2}xy (cm^{2}).$

Bài tập 7 trang 17 sgk Toán 8 tập 1 CD:

Khu vườn của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (Hình 4). Biết diện tích của mảnh đất không trồng rau bằng 475 $m^{2}$. Tính độ dài cạnh x(m) của khu vườn đó.

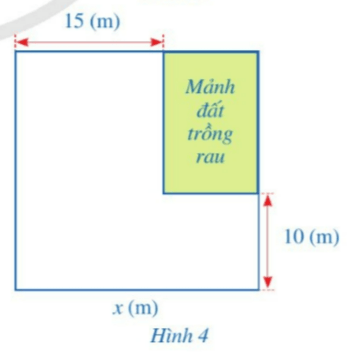
Giair bài tập 7 trang 17 sgk Toán 8 tập 1 CD