Toán 8 Bài 1: Định lí Thalès trong tam giác
Giải Toán 8 Bài 1: Định lí Thalès trong tam giác được VnDoc tổng hợp và đăng tải sau đây bao gồm đáp án và hướng dẫn giải chi tiết cho các câu hỏi trong SGK Toán 8 Cánh diều tập 2, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.
Giải Toán 8 Cánh diều Bài 1: Định lí Thalès trong tam giác
Bài 1 trang 57 Toán 8 Cánh diều tập 2
Cho tam giác ABC có AB = 4,5 cm, AC = 6 cm. Các điểm M, N lần lượt thuộc các cạnh AB, AC thỏa mãn AM = 3 cm và MN // BC. Tính độ dài đoạn thẳng AN.
Hướng dẫn giải
Vì MN // BC nên 
\(\frac{AM}{AB}=\frac{AN}{AC}\) hay \(\frac{3}{4,5}=\frac{AN}{6}\)
Suy ra: AN = 4.
Bài 2 trang 57 Toán 8 Cánh diều tập 2
Cho hình thang ABCD (AB //CD) có AB = 4cm, CD = 6 cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{AM}{MD}=\frac{BN}{NC}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
Hướng dẫn giải
a) Tam giác ACD có MP // CD: \(\frac{AM}{MD}=\frac{AP}{PC}\) (1)
Tam giác ABC có PN // AB: \(\frac{BN}{NC}=\frac{AP}{PC}\) (2)
Từ (1)(2) suy ra: \(\frac{AM}{MD}=\frac{BN}{NC}\).
b) Ta có: MD = 2MA nên \(\frac{AM}{MD}=\frac{1}{2}\) hay \(\frac{AM}{AD}=\frac{1}{3}\)
Mà \(\frac{MP}{CD}=\frac{AM}{AD}\) (MP // CD)
Suy ra: \(\frac{MP}{CD}=\frac{1}{3}\) mà CD = 6 nên MP = 2.
Vì \(\frac{AM}{MD}=\frac{BN}{NC}\) (câu a) nên \(\frac{BN}{NC}=\frac{1}{2}\) hay \(\frac{CN}{BC}=\frac{2}{3}\)
Mà \(\frac{PN}{AB}=\frac{CN}{BC}\)
Suy ra: \(\frac{PN}{AB}=\frac{2}{3}\) mà AB = 4 nên PN = \(\frac{8}{3}\)
Do đó: MN = MP + PN = 2 + \(\frac{8}{3}\) = \(\frac{14}{3}\)
Bài 3 trang 57 Toán 8 Cánh diều tập 2
Trong Hình 15, cho MN //AB, NP // BC. Chứng minh MP // AC.
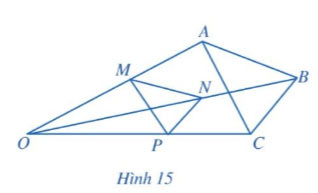
Hướng dẫn giải
MN // AB nên \(\frac{OM}{OA}=\frac{ON}{OB}\)
NP // BC nên \(\frac{OP}{OC}=\frac{ON}{OB}\)
Do đó: \(\frac{OM}{OA}=\frac{OP}{OC}\)
Suy ra: MP // AC (định lí Thalès).
Bài 4 trang 57 Toán 8 Cánh diều tập 2
Trong Hình 16, độ dài đoạn thẳng A'C' mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A', A', B). Giả sử AC = 2m, AB = 1,5 m, A'B = 4,5 m. Tính chiều cao của cây.
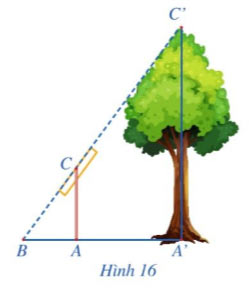
Hướng dẫn giải
Do AC // A'C' (cùng vuông góc với A'B) nên \(\frac{AC}{A'C'}=\frac{AB}{A'B}\)
Suy ra: \(\frac{2}{A'C'}=\frac{1,5}{4,5}\). Do đó A'C' = 6.
Vậy chiều cao của cây là 6 cm.
Bài 5 trang 57 Toán 8 Cánh diều tập 2
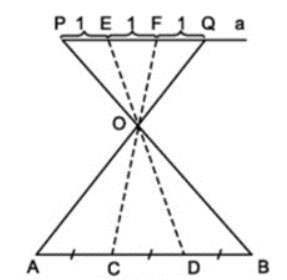
Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không dùng thước để đo.
Hướng dẫn giải
- Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
- E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và AQ.
- Vẽ các đường thẳng EO, FO cắt AB tại C, D.
- Theo hệ quả định lí Thalès ta có:
Tam giác OAC có FQ // AC (F \(\in\) OC, Q \(\in\) OA)
Suy ra: \(\frac{AC}{FQ}=\frac{OA}{OQ}=\frac{OC}{OF}\) (1)
Chứng minh tương tự ta được: \(\frac{CD}{EF}=\frac{OC}{OF}=\frac{OD}{OE}\) (2)
\(\frac{BD}{PE}=\frac{OD}{OE}=\frac{OB}{OP}\) (3)
Từ (1)(2)(3) suy ra: \(\frac{AC}{FQ}=\frac{CD}{EF}=\frac{BD}{PE}\)
Mà PE = EF = FQ = 1. Do đó: AC = CD = BD. (đpcm)
Ngoài Giải Toán 8 Bài 1: Định lí Thalès trong tam giác CD tập 2, mời các bạn tham khảo thêm Đề thi giữa kì 2 lớp 8 hay Đề thi học kì 2 lớp 8 để giúp các bạn học sinh học tốt hơn.
Bài tiếp theo: Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác
