Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Câu hỏi trang 98 Toán 8 Tập 2

Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:

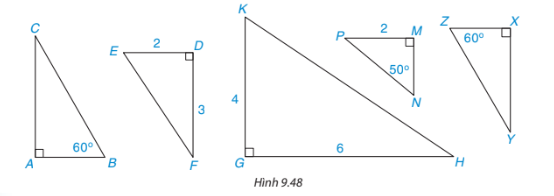
Hướng dẫn giải:

Các cặp tam giác vuông đồng dạng:

\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)

Luyện tập 1 trang 99 Toán 8 Tập 2

Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6m và bóng của Việt dài 70cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy" Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được.

Ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai canh góc vuông của tam giác A'B'C' vuông tại đỉnh A'. Vì các tia sáng mặt trời tạo với hai cái bóng các góc bằng nhau nên \(\widehat B = \widehat {B'}\)

a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?

b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?

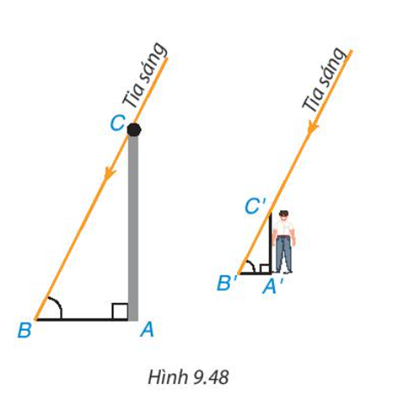
Hướng dẫn giải:

a) Hai tam giác vuông ABC và A'B'C' có \(\widehat B = \widehat {B'}\)

=> ΔABC ∽ ΔA′B′C′

b) Vì ΔABC ∽ ΔA′B′C′

=> \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)

=> \(\frac{{0,7}}{6} = \frac{{1,4}}{{AC}}\)

=> AC=12(m)

Thử thách nhỏ trang 100 Toán 8 Tập 2

Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chấn đến mắt người ấy là 1,6m(H9.51)

A: Vị trí đỉnh cây

B: Vị trí gốc cây

C: Vị trí đỉnh cột.

D: Vị trí mắt

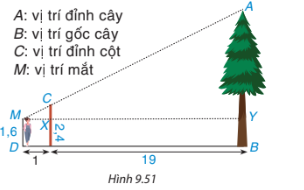
Hướng dẫn giải:

Ta có: CX = 2,4 – 1,6 = 0,8(m)

MN = 1 + 19 = 20 (cm)

Xét tam giác MXC và tam giác MYA có: góc M chung; \(\widehat {M{\rm{X}}C} = \widehat {MY{\rm{A}}}\)

\(\begin{array}{l} \Rightarrow \Delta M{\rm{X}}C \backsim \Delta MY{\rm{A}}\\ \Rightarrow \frac{{M{\rm{X}}}}{{MY}} = \frac{{XC}}{{Y{\rm{A}}}}\\ \Rightarrow \frac{1}{{20}} = \frac{{0,8}}{{Y{\rm{A}}}} \Rightarrow Y{\rm{A}} = 20.0,8 = 16(cm)\\ \Rightarrow AB = BY + Y{\rm{A}} = 1,6 + 16 = 17,6(cm)\end{array}\)

HĐ1 trang 100 Toán 8 Tập 2

Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB=13m, A′B′=6,5m và độ cao lần lượt là BH=5m, B′H′=2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'

- Nhận xét về hai đại lượng \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}}\)

- Dùng định lí Pythagore để tính AH và A'H'

- So sánh các đại lượng \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}}\)

- Hai tam giác vuông A'H'B' và AHB có đồng dạng không

Hướng dẫn giải:

- Có \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)

- Áp dụng định lý Pythagore có \(AH = 12 ;A'H' = 6\)

- Có \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)

=> Hai tam giác vuông A'H'B' và AHB đồng dạng

\(\Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv)\)

Luyện tập 2 trang 102 Toán 8 Tập 2

Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD=6m, AB=4m, HA=2m, AC=1m. Chứng tỏ \(\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\).

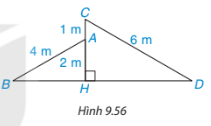
Hướng dẫn giải:

Xét hai tam giác vuông HBA và tam giác HDC nhận thấy:

\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)

=> Hai tam giác đồng dạng

\(\Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)

Vận dụng trang 102 Toán 8 Tập 2

Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không? (Biết rằng 1 inch = 2,54m).

Hướng dẫn giải:

- Gọi chiều ngang của chiếc ti vi mới là x

- Có 55 inch =139,7 cm

- Chiếc ti vi cũ có: chiều ngang màn hình là 72 cm

đường chéo của ti vi là: 32.2,54=81,28 (cm)

Có \(\frac{{81,28}}{{139,7}} = \frac{{72}}{x}\) => x=123,75cm=1,2375m

Vậy không thể đặt vừa chiếc ti vi vào khoảng trống hình vuông cạnh 1m

Bài 9.23 trang 102 Toán 8 KNTT tập 2

Điều kiện nào dưới đây chứng tỏ hai tam giác vuông đồng dạng

a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia

b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia

c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia

d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia

Hướng dẫn giải

Bài 9.24 trang 103 Toán 8 KNTT tập 2

Cặp tam giác vuông nào đồng dạng với nhau trong hình 9.55.

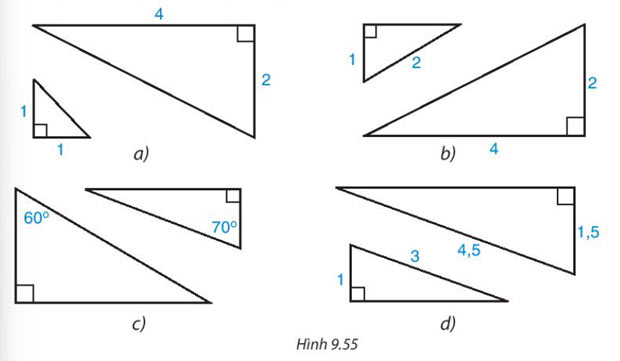
Hướng dẫn giải

Bài 9.25 trang 103 Toán 8 KNTT tập 2

Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh tam giác OAM đồng dạng với tam giác OBN

Hướng dẫn giải

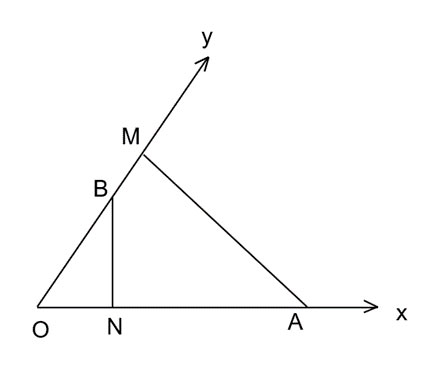
- Xét tam giác OBN có \(\widehat{BON}+\widehat{ONB}+\widehat{NBO}\)=\(180\)°

- Xét tam giác MOA có \(\widehat{MOA}+\widehat{OMA}+\widehat{OMA}\)=\(180\)°

mà \(\widehat{ONB}=\widehat{OMA}=90°\)

góc O chung

=> \(\widehat{NBO}=\widehat{OMA}\)

- Xét hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có: \(\widehat{NBO}=\widehat{OMA}\)

=> ΔOAM ~ ΔOBN

Bài 9.26 trang 103 Toán 8 KNTT tập 2

Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn \(AC=3AB\), \(B'D'=3A'B'\)

a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'

b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là \(2m^{2}\) thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu

Hướng dẫn giải

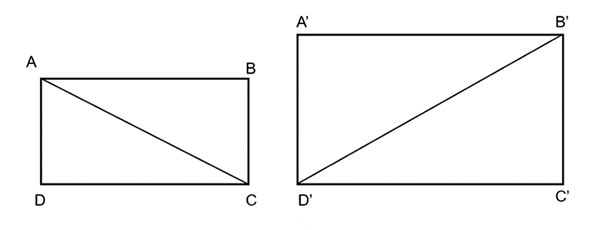
a) Có \(AC=3AB\) => \(\frac{AB}{AC}=\frac{1}{3}\)

- Có \(B'D'=3A'B'\) => \(\frac{A'B'}{B'D'}=\frac{1}{3}\)

=> \(\frac{AB}{A'B'}=\frac{AC}{B'D'}\)

Xét tam giác vuông ABC (vuông tại A) và tam giác vuông A'B'D' (vuông tại C) có

=> \(\frac{AB}{A'B'}=\frac{AC}{B'D'}\)

=> \(ΔABC ~ ΔC'D'B'\) (1)

- Xét \(ΔC'D'B'\) và \(ΔA'B'C'\)

Có B'C' chung, \(A'B'=C'D'\), \(A'C'=B'D'\) (hai hình chéo của chữ nhật)

=> \(ΔC'D'B'=ΔA'B'C'\) (2)

Từ (1) và (2) chung =>\(ΔABC ~ ΔA'B'C'\)

b) - Vì \(A'B'=2AB\) => \(\frac{AB}{A'B'}=\frac{1}{2}\)

mà ΔABC ~ ΔA'B'C' => \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{1}{2}\)

- Có diện tích ABCD là: \(AB.BC\)

Có diện tích A'B'C'D' là: \(A'B'.B'C'\)

=> Xét tỉ lệ hai tam giác ABCD và A'B'C'D', có

\(\frac{AB.BC}{A'B'.B'C'}=\frac{AB}{A'B'}\cdot \frac{BC}{B'C'}=\frac{1}{4}\)

=> \(S_{A'B'C'D'}=4S_{ABCD}\)

mà \(S_{ABCD}=2m^{2}\) => \(S_{A'B'C'D'}=8m^{2}\)

Bài 9.27 trang 103 Toán 8 KNTT tập 2

Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:

a)\(\frac{A'H'}{AH}=k\)

b) Diện tích tam giác A'B'C' bằng \(k^{2}\) lần diện tích tam giác ABC

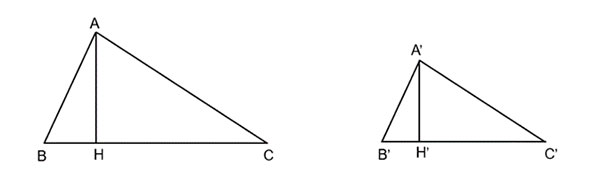
Hướng dẫn giải

a) Vì \(\Delta A'B'C'\) ~ \(\Delta ABC\)

=> \(\widehat{B}=\widehat{B'}\); \(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}=k\)

Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có:

\(\widehat{B}=\widehat{B'}\)

=> \(\Delta A'H'B'\) ~ \(\Delta AHB\)

=> \(\frac{A'H'}{AH}=\frac{A'B'}{AB}\)

mà \(\frac{A'B'}{AB}=k\)

=> \(\frac{A'H'}{AH}=k\)

b) Có diện tích tam giác ABC là: \(\frac{1}{2}AH.BC\)

Có diện tích tam giác A'B'C' là \(\frac{1}{2}A'H'.B'C'\)

Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có: \(\frac{\frac{1}{2}A'H'.B'C'}{\frac{1}{2}AH.BC}=\frac{A'H'}{AH}\cdot \frac{B'C'}{BC}=k.k=k^{2}\)

Bài 9.28 trang 103 Toán 8 KNTT tập 2

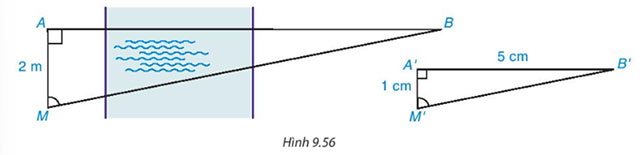
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có AM' = 1cm, \(\widehat{A'M'B'}=\widehat{AMB}\) và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?

Hướng dẫn giải

- Xét \(\Delta A'M'B'\) (vuông tại A) và \(\Delta AMB\) (vuông tại A') có \(\widehat{A'M'B'}=\widehat{AMB}\)

=> \(\Delta A'M'B'\) ~ \(\Delta AMB\)

=> \(\frac{A'M'}{AM}=\frac{A'B'}{AB}\)

=> \(\frac{1}{2}=\frac{5}{AB}\)

=> \(AB=10\) (cm)