Giải Toán 8 trang 82 tập 1 Kết nối tri thức
Giải Toán 8 trang 82 Tập 1
Giải Toán 8 trang 82 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 82.
Hoạt động 1 trang 82 Toán 8 tập 1 Kết nối
Cho DE là đường trung bình của tam giác ABC (H.4.15).
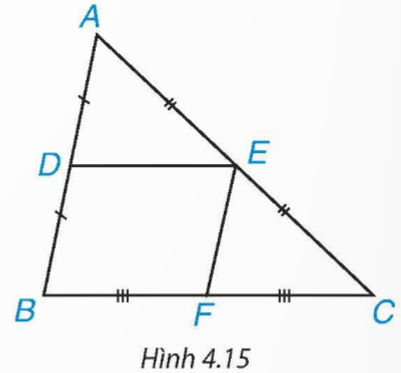
Sử dụng định lí Thales đảo, chứng minh rằng DE // BC.
Hướng dẫn giải:
Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB và AC
Xét tam giác ABC có 
\(\frac{AD}{AB}=\frac{AE}{AC} =\frac{1}{2}\) nên DE // BC (định lí Thales đảo).
Hoạt động 2 trang 82 Toán 8 tập 1 Kết nối
Cho DE là đường trung bình của tam giác ABC (H.4.15).
Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra \(DE=\frac{1}{2}BC\).
Hướng dẫn giải:
Vì DE là đường trung bình của tam giác ABC nên D, E lần lượt là trung điểm của AB và AC.
Xét tam giác ABC có \(\frac{CE}{CA}=\frac{CF}{CB} =\frac{1}{2}\) nên EF // AB (định lí Thales đảo).
Xét tứ giác BDEF có DE // BF và EF // BD nên BDEF là hình bình hành (dhnb).
Do đó DE = BF
Mà \(BF=\frac{1}{2}BC\) nên \(DE=\frac{1}{2}BC\) (đpcm).
-----------------------------------------------
Lời giải Toán 8 trang 82 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức bài 16: Đường trung bình của tam giác, được VnDoc biên soạn và đăng tải!
