Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Toán 8 Luyện tập chung trang 91

Giải Toán 8 Kết nối tri thức tập 2

Bài trước

Tải về

Bài sau

Lớp: Lớp 8

Môn: Toán

Dạng tài liệu: Soạn bài

Bộ sách: Kết nối tri thức với cuộc sống

Loại File: PDF

Phân loại: Tài liệu Tính phí

Giải Toán 8: Luyện tập chung trang 91 trong SGK Toán 8, tập 2, Kết nối tri thức, được biên soạn nhằm hướng dẫn chi tiết cách giải các bài tập trong sách. Tài liệu giúp học sinh luyện tập, củng cố kiến thức đã học, rèn kỹ năng giải toán và nắm chắc các phương pháp, công thức quan trọng. Qua các hướng dẫn cụ thể, các em có thể tự ôn tập, kiểm tra kết quả, đồng thời nâng cao khả năng vận dụng lý thuyết vào bài tập thực hành, từ đó học tốt môn Toán và tự tin chuẩn bị cho các bài học tiếp theo.

Giải Toán 8 KNTT Luyện tập chung trang 91

Bài 9.11 trang 92 Toán 8 Tập 2
Bài 9.12 trang 92 Toán 8 Tập 2
Bài 9.13 trang 92 Toán 8 Tập 2
Bài 9.14 trang 92 Toán 8 Tập 2
Bài 9.15 trang 92 Toán 8 Tập 2

Bài 9.11 trang 92 Toán 8 Tập 2

Cho ΔABC ~ ΔDEF. Biết $\widehat{A}=60°, \widehat{E}=80°$ , hãy tính số đo các góc $\widehat{B}$ , $\widehat{C}$ , $\widehat{D}$ , $\widehat{F}$

Hướng dẫn giải

Vì ΔABC ~ ΔDEF => $\widehat{A}=\widehat{D}$ , $\widehat{B}=\widehat{E}$ , $\widehat{C}=\widehat{F}$

Mà $\widehat{A}=60°$ => $\widehat{D}=60°$

$\widehat{E}=80°$ => $\widehat{B}=80°$

Có $\widehat{A}+\widehat{B}+\widehat{C}=180°$

=> $\widehat{C}=\widehat{F}=180°- 60°- 80°=40°$

Bài 9.12 trang 92 Toán 8 Tập 2

Cho ΔABC ~ ΔA'B'C'. Biết , và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'

Hướng dẫn giải

Có $\frac{AB}{A'B'}=\frac{3}{6}=\frac{1}{2}$

=> ΔABC ~ ΔA'B'C' với tỉ số đồng dạng là $\frac{1}{2}$

=> Chu vi tam giác ABC bằng $\frac{1}{2}$ chu vi tam giác A'B'C'

=> Chu vi A'B'C' là: (cm)

Bài 9.13 trang 92 Toán 8 Tập 2

Cho hình thang ABCD (AB // CD) có $\widehat{DAB}=\widehat{DBC}$

a) Chứng minh rằng ΔABD ~ ΔBDC

b) Giả sử . Tính độ dài các cạnh BC và DC

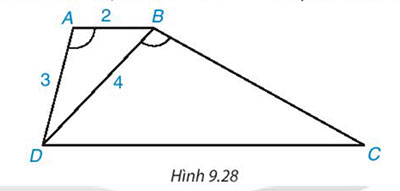
Bài 9.13

Hướng dẫn giải

a) Có AB // CD => $\widehat{ABD}=\widehat{BDC}$

- Xét ΔABD và ΔBDC

Có $\widehat{ABD}=\widehat{BDC}$ , $\widehat{DAB}=\widehat{DBC}$

=> ΔABD ~ ΔBDC (g.g)

b) Có $\frac{AB}{BD}=frac{2}{4}=\frac{1}{2}$

ΔABD ~ ΔBDC với tỉ số $\frac{1}{2}$

=> $\frac{3}{BC}=\frac{4}{DC}=\frac{1}{2}$

=> (cm)

(cm)

Bài 9.14 trang 92 Toán 8 Tập 2

Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, cm, cm. Chứng minh rằng $\Delta AEF$ ~ $\Delta ECD$ và tính tỉ số đồng dạng

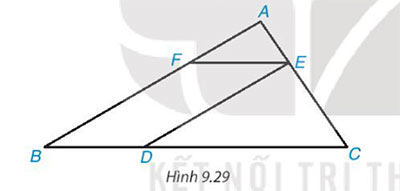
Bài 9.14

Hướng dẫn giải

- Có EF // BC => $\widehat{AEF}=\widehat{ACD}$ (2 góc đồng vị) (1)

- Có EF // BD (vì EF // BC)

DE // FB (vì MN // BC)

=> EFBD là hình bình hành

=> $\widehat{EFB}=\widehat{EDB}$

Mà $\widehat{EFB}+\widehat{AFE}=180°$

$\widehat{EDB}+\widehat{EDC}=180°$

=> $\widehat{AFE}=\widehat{EDC}$ (2)

Từ (1) và (2) => ΔAEF ~ ΔECD (g.g)

Có $\frac{AF}{ED}=\frac{2}{4}=\frac{1}{2}$

=> Đồng dạng với tỉ số $\frac{1}{2}$

Bài 9.15 trang 92 Toán 8 Tập 2

Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng $\widehat{BAC}=\widehat{CDB}$ . Chứng minh rằng ΔAED ~ ΔBEC.

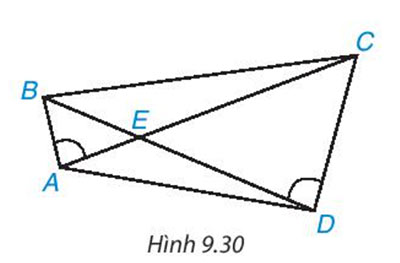
Bài 9.15

Hướng dẫn giải

Xét hai tam giác AEB và DEC có:

$\widehat {BAC} = \widehat {C{\rm{D}}B}$ (giả thiết)

$\widehat {AEB} = \widehat {DEC}$ (đối đỉnh)

Suy ra $\Delta A{\rm{E}}B \backsim \Delta DEC$ (g.g) suy ra:

$\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}$

Xét hai tam giác AED và BEC có:

$\widehat {A{\rm{ED}}} = \widehat {BEC}$ (đối đỉnh)

$\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}$

Suy ra ΔAED ∽ ΔBEC (c.g.c)

Tải về

Chọn file muốn tải về: