Đề cương ôn tập học kì 2 môn Toán lớp 8 năm 2025

Đề cương ôn tập học kì 2 Toán 8 năm 2025 bộ 3 sách mới Chân trời sáng tạo, Kết nối tri thức, Cánh diều tóm tắt lý thuyết kèm bài tập ôn tập đi kèm, dưới dạng trắc nghiệm và tự luận cho các em tham khảo, lên kế hoạch ôn thi, chuẩn bị cho kì thi cuối học kì 2 Toán 8 sắp tới.

Lưu ý: Toàn bộ nội dung đề cương được để trong file tải, mời các bạn tải về tham khảo trọn bộ.

1. Đề cương học kì 2 Toán 8 CTST cấu trúc mới năm 2025

ĐỀ CƯƠNG ÔN TẬP KIỂM TRA HỌC KÌ II MÔN TOÁN 8.

NĂM HỌC 2024 - 2025

A. CÁC KIẾN THỨC TRỌNG TÂM

I. ĐẠI SỐ:

Chương 5: Hàm số và đồ thị

- Khái niệm hàm số. Tọa độ của một điểm và đồ thị của hàm số

- Hàm số bậc nhất y = ax + b (a ¹ 0) . Hệ số góc của đường thẳng

Chương 6: Phương trình

- Phương trình bậc nhất một ẩn

- Giải bài toán bằng cách lập phương trình

II. HÌNH HỌC:

Chương 7: Định lí Thalès

- Định lí Thalès trong tam giác.

- Đường trung bình của tam giác

- Tính chất đường phân giác của tam giác

Chương 8: Hình đồng dạng

- Tam giác đồng dạng

- Các trường hợp đồng dạng của tam giác

- Các trường hợp đồng dạng của hai tam giác vuông. Hình đồng dạng

III. MỘT SỐ YẾU TỐ XÁC SUẤT:

- Mô tả được xác suất bằng tỉ số

- Xác suất lí thuyết và xác suất thực nghiệm

B. CÁC ĐỀ THAM KHẢO

ĐỀ 1.

(Thời gian làm bài: 90 phút)

A. TRẮC NGHIỆM (7,0 điểm).

Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3,0 điểm).
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.

Câu 1: Một hộp đựng 10 tấm thẻ cùng loại được đánh số thứ tự từ 11 đến 20. Lấy ngẫu nhiên một thẻ từ hộp. Các kết quả thuận lợi cho biến cố “Số ghi trên thẻ lấy ra chia hết cho 2” là

A. {12;14;16;18}

B. {12;14;16;18; 20}

C. {12;14}

D. {12;14;16;18;19}

Câu 2: Một hộp chứa 10 tấm thẻ cùng loại được đánh số thứ tự 21 đến 30. Minh lấy ra ngẫu nhiên một thẻ từ hộp. Xác suất nghiệm của biến cố “thẻ chọn ra ghi số nguyên tố” là

A. 0,4

B. 0,3

C. 0,2

D. 0,1

Câu 3: Một hộp chứa 5 viên bi xanh, 3 viên bi đỏ, 6 viên bi vàng. Lấy ngẫu nhiên 1 viên bi.

Tỉ số mô tả xác suất thực nghiệm của biến cố “Viên bi lấy được là viên bi xanh” là

A. 5

9

B. 3

7

C. 3

14

D. 5

14

Câu 4. Một hộp chứa 5 lá thăm cùng loại được đánh số 10; 13; 15; 18; 28. Lấy ngẫu nhiên một lá thăm từ hộp. Xác suất thực nghiệm của biến cố “Lá thăm được lấy ra ghi số lẻ”

A. 0,6

B. 0,4

C. 0,5

D. 0,7

Câu 5. Điểm nào sau đây thuộc đồ thị hàm số y = 5x

A. A(0; 2)

B. B(-1; 5)

C. C(1; -5)

D. D(1; 5)

Câu 6. Tìm m để các hàm số bậc nhất y = mx - 7 và y = 5x + 2 có đồ thị là những đường thẳng song song với nhau

A. m ¹ 5 B. m = -5 C. m = 1 5

D. m = 5

Câu 7. Hãy chọn câu đúng

A. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng hai lần cạnh ấy.

B. Đường trung bình của tam giác thì bằng tổng độ dài ba cạnh của tam giác ấy.

C. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng cạnh ấy.

D. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Câu 8. Cho hình vẽ. Hãy chọn đáp án đúng

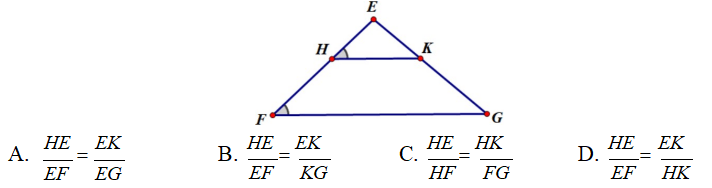
Câu 9. Cho tam giác ABC có AC = 14 cm. Gọi D, E lần lượt là trung điểm của AB, BC. Khi đó độ dài đoạn DE là…

A. 7 cm

B. 8 cm

C. 10 cm

D. 28 cm

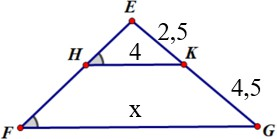
Câu 10: Cho hình vẽ dưới đây biết DE // NP. Độ dài x là

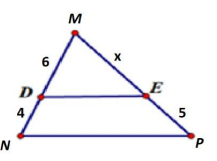
A. 7,5

B. 4,8

C. 8

D. 2,5

Câu 11: Trong các hình sau có bao nhiêu hình thể hiện tính đồng dạng

A. 1 hình

B. 2 hình

C. 3 hình

D. Không có hình nào

Câu 12: Trong các hình sau, hình đồng dạng với hình a là

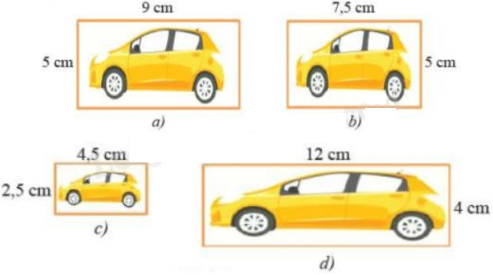
A. Hình b

B, Hình c

C. Hình d

D. Không có hình nào

Phần 2. Câu hỏi trắc nghiệm đúng sai (2,0 điểm)

Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Câu 13. Cho đường thẳng d: y = -2x + 4.

a) Đường thẳng d song song với đường thẳng d1: y = -2x – 4

b) Đường thẳng d đi qua điểm A (0; 4)

c) Đường thẳng d luôn đi qua gốc tọa độ O(0; 0)

d) Đường thẳng d cắt trục tung tại điểm có tung độ bằng - 4

Câu 14. Cho hàm số y = f (x) = x + 3

a. Bảng giá trị

x	0	1
y = x + 3	3	4

b. Đồ thị hàm số y = x + 3 đi qua điểm A(-1; 2)

c) f (-2) = 5

d) Đồ thị hàm số đã cho là đường thẳng song song với trục hoành

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)

Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Giải phương trình 5x + 20 = 0 ta được nghiệm là …

Câu 16. Giải phương trình - 3x - 7 = 2x + 13 ta được nghiệm là …

Câu 17. Cho hình vẽ dưới đây biết AD là đường phân giác. Độ dài x là …

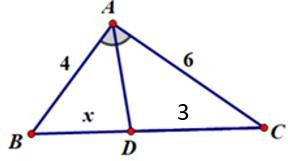
Câu 18. Cho hình vẽ. Độ dài x là …

TỰ LUẬN (3,0 điểm).

Bài 1. (1,0 điểm). Giải bài toán sau bằng cách lập phương trình:

Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 6m. Nếu giảm chiều rộng 2m và tăng chiều dài 4m thì diện tích khu vườn tăng thêm 40m². Tính chiều rộng và chiều dài lúc đầu của khu vườn.

Bài 2. (1,5 điểm). Cho tam giác DEF vuông tại D, kẻ đường cao DH. Chứng minh:

a. ΔDEF ∼ ΔDHDF

b. Biết EF = 15 cm, FH = 5,4 Tính độ dài đoạn thẳng DF

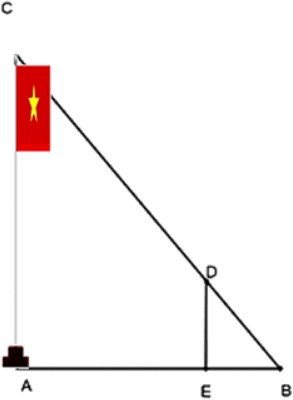
Bài 3. (0,5 điểm). Để đo chiều cao AC của một cột cờ, người ta cắm một cái cọc ED có chiều cao 2m vuông góc với mặt đất. Đặt vị trí quan sát tại B biết khoảng cách BE bằng 1,5 m và khoảng cách AB là 9 m. Tính chiều cao AC của cột cờ.

Mời các bạn xem tiếp Đề 2 trong file tải

2. Đề cương Toán 8 học kì 2 Cánh diều

Phần I. Tóm tắt nội dung kiến thức

A. Thống kê và xác suất

1. Thu thập và phân loại dữ liệu.

2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.

3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ.

4. Xác suất của biến cố ngẫu nhiêu trong một số trò chơi đơn giản.

5. Xác suất thực nghiệm của biến cố ngẫu nhiêu trong một số trò chơi đơn giản.

B. Đại số

1. Phương tình bậc nhất một ẩn.

2. Ứng dụng của phương tình bậc nhất một ẩn.

C. Hình học

1. Định lí Thalès trong tam giác.

2. Đường trung bình của tam giác.

3. Tính chất đường phân giác của tam giác.

4. Tam giác đồng dạng.

5. Các trường hợp đồng dạng của hai tam giác.

6. Các trường hợp đồng dạng của hai tam giác vuông.

7. Hình đồng dạng.

Phần II. Một số câu hỏi, bài tập tham khảo

A. Bài tập trắc nghiệm

Chọn câu trả lời đúng.

Câu 1. Trong các hình thức thu thập dữ liệu sau đây, đâu là hình thức thu thập dữ liệu trực tiếp?

A. Tìm tài liệu có sẵn trên Internet.

B. Quan sát.

C. Tìm thông tin từ trong sách, báo.

D. Tin tức từ TV.

Câu 2. Dữ liệu thu được về size áo bao gồm S, M, L của các nhân viên trong công ty là

A. Số liệu rời rạc.

B. Số liệu liên tục.

C. Dữ liệu không là số, có thể sắp thứ tự.

D. Dữ liệu không là số, không thể sắp thứ tự.

Câu 3. Dự báo quy mô dân số của Trung Quốc và Ấn Độ qua các năm được biểu diễn bằng biểu đồ sau:

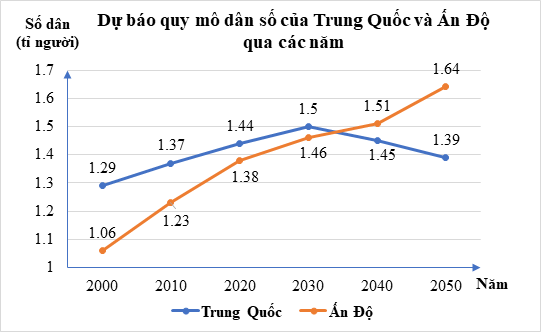
Nhận xét nào trong các nhận xét sau đây là đúng?

A. Dân số Trung Quốc luôn thấp hơn dân số Ấn Độ.

B. Dân số Trung Quốc luôn cao hơn dân số Ấn Độ.

C. Hiện tại dân số Trung Quốc cao hơn nhưng sẽ thấp hơn dân số Ấn Độ trong tương lai.

D. Hiện tại dân số Trung Quốc thấp hơn nhưng sẽ cao hơn dân số Ấn Độ trong tương lai.

Câu 4: Trong các phương trình sau, đâu là phương trình bậc nhất một ẩn

A. \(3x - y = 0\).

B. \(2y + 1 = 0\).

C. \(4 + 0.x = 0\).

D. \(3{x^2} = 0\).

Câu 5: Phương trình bậc nhất một ẩn \(ax + b = 0\) với hệ số b = 3 là phương trình nào

A. \(3x + 1 = 0\).

B. \(x - 3 = 0\).

C. \(- x + 3 = 0\).

D. \(3x - 3 = 0\).

Câu 6: Phương trình \(6x - 3 = 0\) có nghiệm là

A. \(x = 2\).

B. \(x = - \frac{1}{2}\).

C. \(x = - 2\).

D. \(x = \frac{1}{2}\).

Câu 7: Đưa phương trình \(2\left( {x + 2} \right) = 1 - 2x\) về dạng \(ax + b = 0\), ta được:

A. \(4x + 3 = 0\).

B. \(- 2x + 1 = 0\).

C. \(4x + 5 = 0\).

D. \(2x + 4 = 0\).

Câu 8: Tập nghiệm S của phương trình \(3\left( {x + 1} \right) + 2x = 7 + \left( {x - 2} \right)\) là:

A. \(S = \left\{ 0 \right\}\).

B. \(S = \left\{ {\frac{1}{2}} \right\}\).

C. \(S = \emptyset\).

D. \(S = \mathbb{R}\).

Câu 9: Phương trình \(2x + m - x + 4 = 0\) nhận \(x = - 3\) thì m là :

A. \(m = 1\).

B. \(m = 2\).

C. \(m = - 1\).

D. \(m = - 2\).

Câu 10: Chọn câu sai trong các câu sau:

A. Gọi số học sinh của một lớp là x (học sinh thì điều kiện là \(x \in N*\).

B. Gọi thời gian làm của một xưởng là x (ngày) thì điều kiện là \(x > 0\).

C. Gọi số bài tập của một học sinh làm trong một ngày là x thì điều kiện là \(x < 0\).

D. Gọi tốc độ của một xe ô tô là x thì điều kiện của x là \(x > 0\).

Câu 11: Xe máy đi từ A đến B với vận tốc \(x\left( {km/h} \right)\). Ô tô đi từ B về A với vận tốc nhanh hơn vận tốc của xe máy là \(15km/h\). Vậy vận tốc của ô tô được biểu diễn theo x là:

A. \(x - 15\left( {km/h} \right)\).

B. \(15x\left( {km/h} \right)\).

C. \(15 - x\left( {km/h} \right)\).

D. \(x + 15\left( {km/h} \right)\).

Câu 12: Trên một khúc sông, một chiếc thuyền chạy với vận tốc tối đa đang di chuyển xuôi dòng, một người đứng trên bờ đo được vận tốc của chiếc thuyền là 35km/h. Biết vận tốc dòng nước là 5km/h. Hỏi nếu thuyền đó chạy ngược dòng với vận tốc tối đa thì người đứng trên bờ đo được vận tốc của thuyền lúc đó là bao nhiêu?

A. 30km/h.

B. 35km/h.

C. 40km/h.

D. 70km/h.

Câu 13: Cho \(\Delta ABC\backsim \Delta DEF\) theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?

A. \(k = \frac{{AB}}{{BC}}\).

B. \(k = \frac{{AC}}{{DF}}\).

C. \(k = \frac{{DE}}{{AB}}\).

D. \(k = \frac{{DE}}{{DF}}\).

Câu 14: Điểm nằm trên trục hoành có tung độ bằng bao nhiêu?

A. -1.

B. 1.

C. 0.

D. 5.

Câu 15: Tam giác ABC có HK là đường trung bình \(\left( {H \in AC,K \in BC} \right)\). Khi đó \(\Delta ABC\backsim \Delta HKC\) theo tỉ số k bằng bao nhiêu?

A. \(k = 2\).

B. \(k = \frac{1}{2}\).

C. \(k = 1\).

D. \(k = 0\).

Câu 16: Cho \(\Delta ABC\backsim \Delta DEF\). AM, AN lần lượt là hai tia phân giác của \(\widehat A,\widehat D\). Khi đó \(\Delta ABM\backsim \Delta DEN\) theo trường hợp nào?

A. góc - góc.

B. cạnh – góc – cạnh.

C. cạnh – cạnh – cạnh.

D. cạnh huyền – góc nhọn.

Câu 17: Cho \(\Delta ABC\backsim \Delta DEF\) theo tỉ số đồng dạng k = 2. Khi đó chu vi \(\Delta ABC\) gấp mấy lần chu vi \(\Delta DEF\)?

A. 1.

B. 2.

C. 4.

D. 8.

Câu 18: Cho tam giác ABC có M, N lần lượt nằm trên cạnh AB, AC sao cho MN // BC. Biết AM = 16cm, AN = 20cm, NC = 15cm. Khi đó độ dài AB bằng:

A. 28cm.

B. 26cm.

C. 24cm.

D. 22cm.

Câu 19: Cho hình thang ABCD (AB // CD), có hai đường chéo AC và BD cắt nhau tại I. Biết AB = 16cm, CD = 40cm. Khi đó \(\Delta AIB\backsim \Delta CID\) với tỉ số:

A. \(k = \frac{2}{3}\).

B. \(k = \frac{3}{2}\).

C. \(k = \frac{2}{5}\).

D. \(k = \frac{5}{2}\).

Câu 20:Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm , 8cm và 10cm Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

A. 6cm, 12cm, 15cm.

B. 8cm, 16cm, 20cm.

C. 6cm, 9cm, 18cm.

D. 8cm, 10cm, 15cm.

Câu 21: \(\Delta ABC\backsim \Delta A'B'C'\) theo tỉ số đồng dạng k = 3 thì tỉ số chiều cao h của \(\Delta ABC\) với chiều cao h’ của \(\Delta A'B'C'\) là:

A. \(\frac{h}{{h'}} = \frac{1}{3}\).

B. \(\frac{h}{{h'}} = 6\).

C. \(\frac{h}{{h'}} = - 3\).

D. \(\frac{h}{{h'}} = 3\).

B. Bài tập tự luận

Bài 1. Nhóm của Nam phát tờ khảo sát về số điểm 10 các bạn trong lớp đã đạt trong kỳ thi vừa rồi. Nhóm của Nam đã sử dụng phương pháp thu thập dữ liệu nào? Nếu nhóm Nam sử dụng phương pháp thu thập dữ liệu còn lại thì sẽ thực hiện như thế nào?

Bài 2. Dữ liệu thu được cho mỗi câu hỏi sau thuộc loại nào?

a) Cân nặng của bạn là bao nhiêu?

b) Số sản phẩm nhà máy sản xuất được trong tháng là bao nhiêu?

c) Vị kem yêu thích nhất của bạn là gì?

d) Bạn đánh giá đề thi học kì 1 như thế nào trong các mức độ sau: rất khó, khó, trung bình, dễ, rất dễ?

Bài 3. Biểu đồ tranh dưới đây biểu diễn giá vé của một rạp xiếc ở Mỹ tương ướng với 3 loại vé A, B và C.

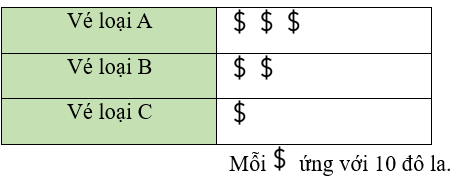
Vẽ biểu đồ cột để biểu diễn dữ liệu này.

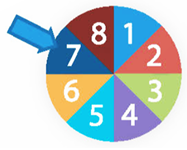
Bài 4. Trên bàn có một tấm bìa hình tròn được chia thành 8 hình quạt bằng nhau và được đánh số từ 1 đến 8 (như hình vẽ). Xoay tấm bìa quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Xét các biến cố sau:
A: "Mũi tên chỉ vào ô ghi số chẵn"; B: "Mũi tên chỉ vào ô ghi số chia hết cho 4"; C: "Mũi tên chỉ vào ô ghi số nhỏ hơn 3". Hãy nêu các kết quả thuận lợi cho mỗi biến cố trên.

Bài 5. Lớp 8A gồm 34 học sinh, trong đó có 16 bạn nữ. Có 6 bạn nữ tham gia câu lạc bộ đọc sách và 8 bạn nam không tham gia câu lạc bộ đọc sách. Chọn ngẫu nhiên một học sinh trong lớp. Tính xác suất để học sinh đó là một bạn nam có tham gia câu lạc bộ đọc sách.

Bài 6. Một hộp chứa các viên bi màu trắng và đen có kích thước và khối lượng như nhau. Mai lấy ra ngẫu nhiên từ một hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 80 lần, Mai thấy có 24 lần lấy được viên bi màu trắng.

a) Hãy tính xác suất thực nghiệm của biến cố "Lấy được viên bi màu đen" sau 80 lần thử.

b) Biết tổng số bi trong hộp là 10, hãy ước lượng xem trong hộp có khoảng bao nhiêu viên bi trắng.

Bài 7. Giải các phương trình sau:

a) \(7x - 4 = 0\)

b) \(9 - 5x = 0\)

c) \(11x - \left( {3x + 3} \right) = 8\left( {x - 2} \right)\)

d) \(\frac{{2x - 1}}{5} + x = 3 + \frac{{3 - x}}{4}\)

Bài 8. Tìm m để phương trình \(\left( {m - 1} \right)x = {m^2} - 1\)

a) Vô nghiệm.

b) Vô số nghiệm.

c) Có nghiệm duy nhất.

Bài 9. Bác An đầu tư 500 triệu đồng vào hai tài khoản: mua trái phiếu doanh nghiệp với lãi suất 8% một năm và gửi tiết kiệm ngân hàng với lãi suất 6% một năm. Cuối năm bác An nhận được 34 triệu đồng tiền lãi. Hỏi bác An đã đầu tư vào mỗi tài khoản bao nhiêu tiền?

Bài 10. Một xe tải đi từ M đến N với tốc độ 50 km/h. Khi từ N quay về M xe chạy với tốc độ 40 km/h. Thời gian cả đi lẫn về mất 5 giờ 24 phút không kể thời gian nghỉ. Tính chiều dài quãng đường MN.

Bài 11. Cho \(\Delta KBC\) vuông tại K có KB < KC. Tia phân giác của \(\widehat B\) cắt KC tại H . Qua C vẽ đường thẳng vuông góc với tia BH tại I .

a) Chứng minh \(\Delta BHK\backsim \Delta CHI\).

b) Chứng minh \(C{I^2} = IH.IB\).

c) Tia BK cắt CI tại A, tia AH cắt BC tại D .

Chứng minh KC là phân giác của \(\widehat {IKD}\).

Bài 12. Cho ΔABC vuông tại A, biết \(AB = 3cm,BC = 5cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.

a) Vẽ tia Cx vuông góc với BD tại E và tia Cx cắt đường thẳng AB tại F.

Chứng minh \(\Delta ABD\backsim \Delta EBC\).

b) Tia FD cắt BC tại H. Kẻ đường thẳng qua H và vuông góc với AB tại M.

Chứng minh \(MH.AB = FH.MB\).

Bài 13. Cho ΔABC vuông tại A có AB < AC , đường cao AH .

a) Chứng minh \(\Delta HAC\backsim \Delta ABC\)

b) Chứng minh \(H{A^2} = HB.HC\)

c) Gọi D và E lần lượt là trung điểm của AB, BC.

Chứng minh \(CH.CB = 4.D{E^2}\)

d) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và đường thẳng DE . Gọi N là giao điểm của AH và CM . Chứng minh N là trung điểm của AH.

Bài 14*. Giải phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\)

Bài 15*. Cho các số thực a, b, c thỏa mãn abc = 2024. Tính giá trị của biểu thức:

\(P = \frac{{2bc - 2024}}{{3c - 2bc + 2024}} - \frac{{2b}}{{3 - 2b + ab}} + \frac{{4048 - 3ac}}{{3ac - 4048 + 2024a}}\)

Bài 16. Cho 2024 số: \({a_1},{a_2},...,{a_{2024}}\) với \({a_k} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}}\) \(\left( {k = 1,2,...,2024} \right)\).

Tính giá trị biểu thức \(A = {a_1} + {a_2} + ... + {a_{2024}}\).

3. Đề cương ôn tập học kì 2 Toán 8 KNTT

Phần I. Lý thuyết

A. Đại số

1. Khái niệm phân thức đại số.

2. Tính chất cơ bản của phân thức đại số.

3. Phép cộng và phép trừ phân thức đại số.

4. Phép nhân và phép chiaphân thức đại số.

5. Phương tình bậc nhất một ẩn.

5. Giải bài toán bằng cách lập phương trình.

6. Khái niệm hàm số và đồ thị của hàm số.

7. Hàm số bậc nhất và đồ thị của hàm số bậc nhất.

8. Hệ số góc của đường thẳng.

B. Thống kê và xác suất

1. Kết quả có thể và kết quả thuận lợi.

2. Cách tính xác suất của biến cố bằng tỉ số.

3. Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng.

C. Hình học

1. Hai tam giác đồng dạng.

2. Ba trường hợp đồng dạng của hai tam giác.

3. Định lí Pythagore và ứng dụng.

4. Các trường hợp đồng dạng của hai tam giác vuông.

5. Hình đồng dạng.

6. Hình chóp tam giác đều.

7. Hình chóp tứ giác đều.

Phần II. Một số câu hỏi, bài tập tham khảo

Mời các bạn xem tiếp trong file tải