Bộ 12 đề thi học kì 2 Toán 8 Sách mới - Có đáp án

Đề thi cuối kì 2 Toán 8 Sách mới

Bộ đề thi Toán 8 học kì 2 năm 2025 Sách mới bao gồm 12 đề thi khác nhau, có đáp án và ma trận do thư viện đề thi VnDoc.com tổng hợp và đăng tải. Đây là tài liệu hay cho thầy cô tham khảo ra đề thi học kì 2 Toán 8. Đây cũng là tài liệu giúp các em ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài tập Toán để đạt điểm cao trong kỳ thi sắp tới.

 Lưu ý: Toàn bộ 12 đề thi và đáp án đều có trong file tải, mời các bạn tải về tham khảo trọn bộ.

Hoặc có thể tải miễn phí theo từng đề theo link sau:

• Đề thi học kì 2 Toán 8 Cánh diều
• Đề thi học kì 2 Toán 8 Chân trời sáng tạo
• Đề thi học kì 2 Toán 8 Kết nối tri thức

1. Đề thi cuối kì 2 Toán 8 Cánh diều

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Mỗi câu lạc bộ tại trường Trung học Sao Mai có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây:

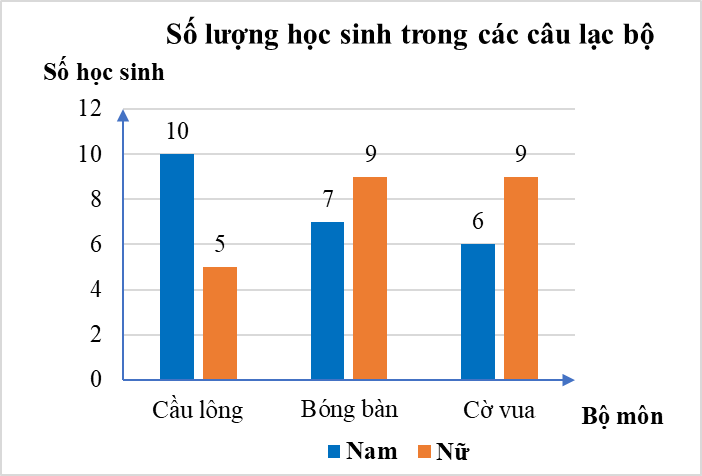
Biết trong biểu đồ, dữ liệu thống kê của một câu lạc bộ chưa chính xác, đó là

A. Cầu lông.

B. Bóng bàn.

C. Cờ vua.

D. Không có dữ liệu chưa chính xác trong biểu đồ.

Câu 2: Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?

A. 1

B. \(\frac{1}{4}\)

C. \(\frac{1}{5}\)

D. 5

Câu 3. Phương trình nào sau đây là phương trình bậc nhất một ẩn?

A. 0x + 5 = 0.

B. x² - 4 = 0.

C. \(\frac{1}{2} x -3 = 0\)

D. x³ - x + 2 = 0

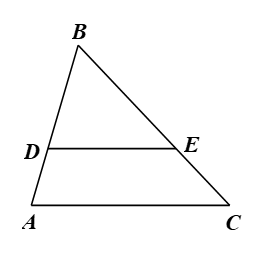
Câu 4. Cho hình vẽ bên, biết DE // AC. Tỉ số nào sau đây là đúng? A. BD/AD=BE/BC. B. BD/AD=BE/EC. C. DE/AC=BC/BE. D. AD/AB=BC/EC.

Câu 5. Cho các mệnh đề sau:

(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

(II) Nếu một cạnh góc vuông của tam giác vuông này bằng một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông ấy đồng dạng.

Hãy chọn đáp án đúng:

A. Cả (I) và (II) đều đúng.

B. Chỉ có (II) đúng.

C. Chỉ có (I) đúng.

D. Cả (I) và (II) đều sai.

Câu 6. Cho ∆RSK và ∆RSK có RSPQ=RKPM=SKQM, khi đó ta có

A. ∆RSK ᔕ ∆MPQ.

B. ∆RSK ᔕ ∆PQM.

C. ∆RSK ᔕ ∆QPM.

D. ∆RSK ᔕ ∆QMP.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,0 điểm) Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối năm 2020.

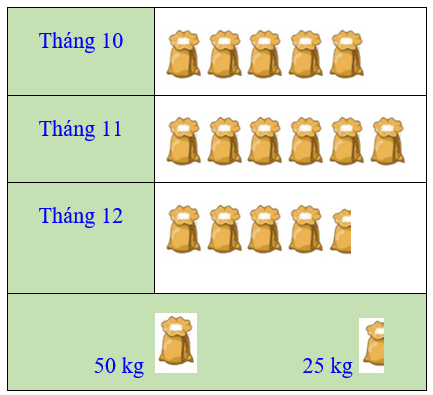
a) Lập bảng thống kê số gạo bán được của một cửa hàng trong ba tháng cuối năm 2020 theo mẫu sau:

Năm	Tháng 10	Tháng 11	Tháng 12
Số gạo bán được (kg)

b) Hãy hoàn thiện biểu đồ ở hình bên dưới để nhận biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh.

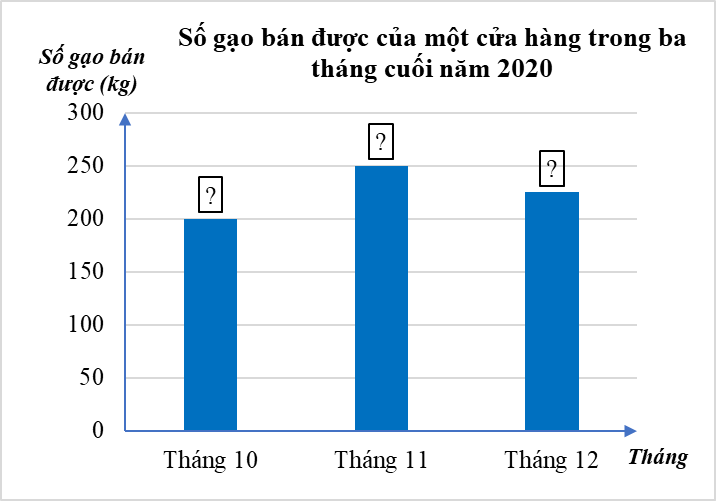
Bài 2. (1,5 điểm) Hiệu hai số là 12. Nếu chia số bé cho 7 và lớn cho 5 thì thương thứ nhất lớn hơn thương thứ hai là 4 đơn vị. Tìm hai số đó.

Bài 3. (1,0 điểm) Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Nhà giáo Việt Nam 20/11, cô giáo đã chọn ra 10 học sinh gồm 4 học sinh nữ nữ là Hoa; Mai; Linh; My; 6 học sinh nam là Cường; Hường; Mỹ; Kiên; Phúc; Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm 10 học sinh tập múa trên.

a) Tìm số phần tử của tập hợp M gồm các kết quả xảy ra đối với tên học sinh được chọn ra.

b. Tính xác suất của các biến cố “Học sinh được chọn ra là học sinh nam”

Bài 4. (1,0 điểm)

Giải bài toán bằng cách lập phương trình

Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.

Bài 5. (2,0 điểm)

Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H

a) Chứng minh \(\Delta ABE\backsim \Delta ACF\)

b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).

c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.

Bài 6. (0,5 điểm)

Cho ba số thực a, b, c khác 2 thỏa mãn a + b + c = 6. Tính giá trị của biểu thức:

\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)

2. Đề thi cuối kì 2 Toán 8 Chân trời sáng tạo

PHẦN A. TRẮC NGHIỆM (2 điểm) . (Học sinh ghi câu trả lời vào giấy làm bài)

Mỗi câu đúng hs được 0.25đ

Câu 1: Hàm số nào dưới đây là hàm số bậc nhất?

A. y = 0x + 1.

B.y = 2x² + 1.

C. y = 5x - 1.

D. y = x² + x + 1.

Câu 2: Trong các hàm số y = 5;y =x² + 1;y = x² + 2x + 1;y = x + 2;y = 3x có bao nhiêu hàm số là hàm số bậc nhất?

A. 1

B. 2

C. 3

D. 4

Câu 3: Khẳng định đúng về đồ thị hàm số y = ax + b (a ≠ 0) với b = 0?

A. Là đường thẳng đi qua gốc tọa độ.

B. Là đường thẳng song song với trục hoành.

C. Là đường cong đi qua gốc tọa độ.

D. Là đường thẳng đi qua hai điểm A(1;b) và B(-b/a;0).

Câu 4: Chọn đáp án đúng

A. Đường trung bình của tam giác là đường thẳng giữa tam giác nối hai cạnh của tam giác đó.

B. Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm.

C. Đường trung bình của tam giác là đoạn thẳng nằm giữa tam giác.

D. Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác đó.

Câu 5: Tính x trong hình sau:

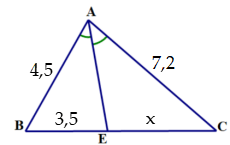
A. 2.1875

B. 9,3

C. 9.26

D. 5,6

Câu 6: Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:

Màu bút	Bút xanh	Bút vàng	Bút đỏ
Số lần	14	10	16

Xác suất thực nghiệm của sự kiện không lấy được màu vàng là:

A. 0,25

B. 0,1

C. 0,75

D. 0,9

Câu 7: Phương trình: 3x + 6 = 0 có nghiệm là số nào?

A. 2

B.– 2

C. 3

D. - 3

Câu 8: Biến đổi phương trình 2x + 4 = 3x – 1 ta được phương trình nào?

A. x – 5 = 0

B.x – 4 = 0

C. 5x + 5 = 0

D. 5x + 3 = 0

PHẦN B. TỰ LUẬN (8 điểm )

Bài 1: (1 điểm) Cho hàm số y = f(x) = 2x +12

a) Tính f(-2); f(2) – f(0)

b) Điểm B(2; 16) có thuộc đồ thị của hàm số y = f(x) không? Vì sao?

Bài 2: (1.5 điểm) Cho hàm số y = -2x có đồ thị là đường thẳng d.

a) (0,5đ) Viết hai hàm số bậc nhất có đồ thị song song với đường thẳng d.

b) (0,5đ) Viết hai hàm số bậc nhất có đồ thị cắt đường thẳng d.

c) Hàm số y = ax + b có đồ thị là đường thẳng m đi qua hai điểm A(0; 3) và B(-1; -2). Tìm a, b.

Bài 3: (0.5 điểm) Giải phương trình sau: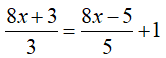

Bài 4: (1.0 điểm) Một xe máy đi từ A đến B với vận tốc 50km/h. Đến B người đó nghỉ 15 phút rồi quay về A với vận tốc 40km/h. Biết thời gian tổng cộng hết 2 giờ 30 phút. Tính quãng đường AB.

Bài 5: (1.0 điểm) Cho tam giác ABC có AB = 6cm, AC = 9cm, BC = 12cm. Trên AB và AC lần lượt lấy hai điểm M và N sao cho AM = 2cm , CN = 6cm.

a) Chứng minh rằng: MN // BC, tính MN

b) Gọi E và F lần lượt là trung điểm AB và BC. Tính EF.

Bài 6: (1.0 điểm) Bóng của một ống khói nhà máy trên mặt đất có độ dài là . Cùng thời điểm đó, một thanh sắt cao cắm vuông góc với mặt đất có bóng dài . Tính chiều cao của ống khói.

Bài 7: (2.0 điểm) Cho tam giác ABC nhọn (AB < AC). Ba đường cao AD, BE, CF cắt nhau tại H.

a. Chứng minh ΔABE ∼ ΔACF. Từ đó suy ra AE.AC = AF.AB .

b. Vẽ DK vuông góc với AC tại K, DK cắt CF tại I. Chứng minh: \(\frac{IK}{ID} = \frac{HE}{HB}\)

3. Đề thi cuối kì 2 Toán 8 Kết nối tri thức

3.1 Đề thi cuối kì 2 Toán 8 KNTT - Đề 1

I. TRẮC NGHIỆM (5,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau:

Câu 1. (NB) Cách viết nào sau đây không cho một phân thức?

Câu 2. (NB) Phân thức: \(-\frac{5x}{5-5x}\) rút gọn thành:

Câu 3. (NB) Giá trị x = - 4 là nghiệm của phương trình:

A. -2,5x + 1 = 11.

B. -2,5x = -10.

C. 3x – 8 = 0.

D. 3x – 1 = x + 7.

Câu 4. (NB) Năm nay Trang x tuổi, tuổi của Trang 6 năm sau là

A. 14.

B. 6+x.

C. 6x.

D. 20.

Câu 5.(NB)Trong các hàm số sau đây hàm số nào là hàm số bậc nhất?

A. y = \(\frac{2}{x}+3\)

B. y = 2mx + 3

C. y = 0x + 2

D. y = (m - 1)x + 2 (m ≠1).

Câu 6.(NB) Đường thẳng nào sau đây song song với đường thẳng ?

A. y = -3x - 1

B. y = 1 - 3x

C. y = -3 + 3x

D. y = 3 - 3x

Câu 7.(TH) Điểm thuộc đồ thị hàm số y = 2x-5 là

A. (4;3) .

B. (3;-1) .

C. (-4;-3).

D.(2;1).

Câu 8.(TH) Cho ABC có Â = 400; \(\hat{B}\) = 800 và DEF có \(\hat{E}\)= 400; \(\hat{D}\)= 600. Khẳng định nào sau đây đúng?

A. ΔABC ∼ ΔDEF.

B. ΔABC ∼ Δ EFD.

C. ΔABC ∼ ΔDFE.

D. ΔDEF ∼ ΔCBA.

Câu 9.(NB) Nếu ΔABC ∼ ΔDEF thì ta có:

Câu 10.(NB) Trong các cặp hình vuông, cặp hình chữ nhật, cặp hình thoi, cặp hình bình hành. Cặp hình nào là cặp hình đồng dạng?

A. Cặp hình vuông.

B. Cặp hình chữ nhật.

C. Cặp thình thoi.

D. Cặp hình bình hành.

Câu 11.(NB) Bộ ba số nào sau đây không phải là độ dài ba cạnh của một tam giác vuông?

A. 1cm, 1cm, \(\sqrt{2}\)cm

B. 4cm, 6cm, 8cm

C. 2cm, 4cm, \(\sqrt{20}\)cm

D. 3cm, 4cm, 5cm

Câu 12.(NB) Một hộp đựng các tấm thẻ ghi số 11, 12, 13,…, 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Xác suất để rút được một tấm thẻ ghi số nguyên tố là

A. 0,2.

B. 0,4.

C. 0,5.

D. 0,6.

Câu 13.(NB) Chọn ngẫu nhiên một số có một chữ số, xác suất để chọn được số chính phương là

A. 0,2.

B. 0,3.

C. 0,4.

D. 0,5.

Câu 14.(TH) Một lồng đèn có dạng hình chóp tứ giác đều có cạnh đáy bằng 15 cm, độ dài trung đoạn bằng 10 cm. Diện tích giấy dán kín bốn mặt bên của lồng đèn (mép dán không đáng kể) là

A. 200 cm².

B. 300 cm².

C. 400 cm².

D. 500 cm².

Câu 15. (NB) Hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S bằng:

II. TỰ LUẬN (5,0 điểm).

Câu 1 (1,0 điểm): Tính

Câu 2 (1,0 điểm) Cho hàm số y = 2x+3 có đồ thị là đường thẳng (d).

a) Cho biết hệ số góc của đường thẳng (d) và góc tạo bởi (d) với trục Ox là góc gì?.

b) Vẽ đường thẳng (d).

Câu 3 (1,0 điểm): Giải bài toán sau bằng cách lập phương trình.

Trong giải bóng đá Hội khỏe phù đổng trường Nguyễn Du có 7 đội bóng tham gia đá vòng tròn 1 lượt (cứ 1 đội gặp 6 đội còn lại, thắng được 3 điểm, hòa được 1 điểm, thua không có điểm). Khi kết thúc giải, đội bóng lớp 8A không thua trận nào và được 14 điểm. Hỏi đội bóng lớp 8A thắng bao nhiêu trận.

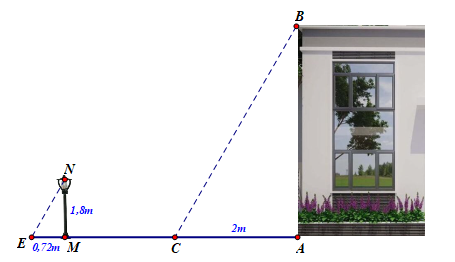
Câu 4 (2,0 điểm): Bóng của một ngôi nhà trên mặt đất có độ dài AC = 2 m. Cùng thời điểm đó, một cột đèn MN = 1,8 m có bóng dài EM = 0,72 m.

a) Chứng minh DABC đồng dạng với DMNE.

b) Tính chiều cao AB của ngôi nhà.

c) Bác An muốn làm một cái thang để lên mái nhà, em hãy tính giúp bác An phải làm cái thang dài bao nhiêu? (Biết để an toàn thì chân thang phải đặt cách chân tường 1,5 m, chiều dài làm tròn đến m).

-------------------- HẾT --------------------

3.2 Đề thi cuối kì 2 Toán 8 KNTT - Đề 2

Ma trận đề thi giữa kì 2 Toán 8 năm 2024

Đề thi học kì 2 Toán 8 KNTT

Phần I. TRẮC NGHIỆM (3,0 điểm).

Mỗi câu sau đây đều có 4 lựa chọn, trong đó chỉ có một phương án đúng.

Hãy viết vào giấy kiểm tra chữ cái A, B, C hoặc D đứng trước câu trả lời mà em chọn.

Câu 1 (NB): Điều kiện để cho biểu thức \(\frac{-2}{x - 5}\)là một phân thức là:

A. x5;

B. x = 5;

C. x 0

D. x = 0

Câu 2 (TH): Phân thức \(\frac{x-2}{x^{2}-4 }\) bằng phân thức nào sau đây?

A. \(\frac{1}{x-2}\)

B. \(\frac{1}{x+2}\)

C.x - 2

D. x + 2

Câu 3 (NB): Cho hình vẽ bên. Đường thẳng OK là đồ thị của hàm số:

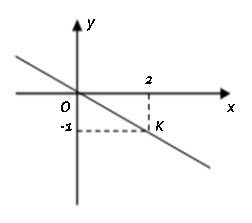
A. y = - 2 x +1

B. y = - 0,5x

C. y = \(-\frac{1}{2}\)x

D. y = 2x - 3

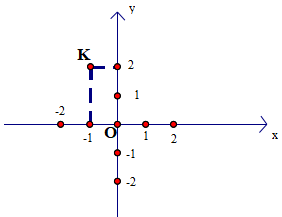
Câu 4 (TH): Trong hình vẽ bên, tọa độ của điểm K là :

A. K(2; -1) B. K(-1; 0) C. K(0; 2) D. K(-1; 2)

Câu 5 (NB): Hệ số góc của đường thẳng y =2 - 5x là:

A. 2

B. 5

C. - 5

D. -3

Câu 6 (NB): Hình chóp tứ giác đều có số mặt là :

A. 4

B. 5

C. 6

D. 7

Câu 7 (VD): Giá trị của x trong hình vẽ sau là

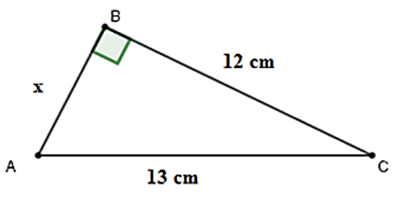
A. 10 cm

B. 11cm

C.8 cm

D. 5 cm

Câu 8 (VDC): Bóng của một tòa nhà trên mặt đất có độ dài 6m. Cùng thời điểm đó, một cọc sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1,5m. Chiều cao của tòa nhà là:

A. 4,5m

B. 6,5m

C.8 m

D. 18 m

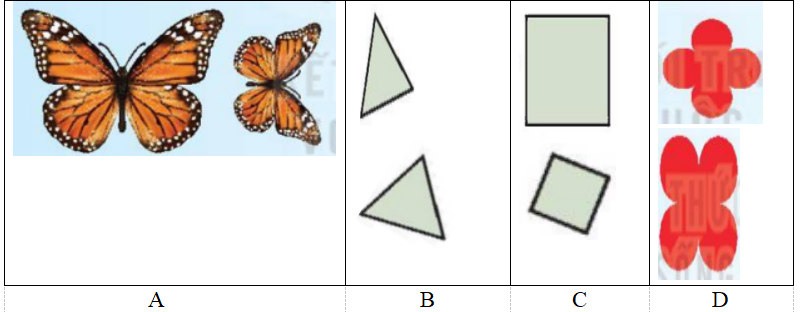
Câu 9 (NB): Trong các hình sau hình nào có hai hình đồng dạng?

Câu 10 (NB): Một chiếc thùng kín đựng một số quả bóng màu đỏ, màu xanh, màu tím, màu vàng có cùng kích thước. Trong một trò chơi, người chơi lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. An thực hiện trò chơi được kết quả ghi lại ở bảng sau:

Màu	Xanh	Đỏ	Tím	Vàng
Số lần	10	6	14	20

Xác suất lớn nhất là ta có thể lấy được quả bóng màu gì?

A. màu đỏ

B. màu xanh

C. màu tím

D. màu vàng

Câu 11 (NB): Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 16%. Gặp ngẫu nhiên một học sinh, xác suất học sinh đó không bị cận thị là:

A. 16%

B. 94%

C. 84%

D. 50%

Câu 12 (VD): Một hộp chứa các thẻ màu xanh và thẻ màu đỏ có kích thước và khối lượng như nhau. Lan lấy ra ngẫu nhiên một thẻ từ hộp, xem màu và trả lại hộp. Lặp lại thử nghiệm đố 50 lần, Lan thấy có 14 lần lấy được thẻ màu xanh. Xác xuất thực nghiệm của biến cố “lấy được thẻ màu đỏ” là:

A. 0,14

B. 0,28

C. 0,72

D. 0,36

Phần II. TỰ LUẬN (7,0 điểm).

Câu 13 (1,0 điểm):

a) (VD) Thực hiện phép tính :

b) (VD) Giải phương trình :

Câu 14 (1,5 điểm): Cho hàm số y = -2x + 1 ( có đồ thị là d)

a) (TH)Tính giá trị của hàm số trên khi x = -1

b) (TH) Tìm giá trị của m để đường thẳng (d) song song với đường thẳng (d’): y = (m +1)x + 2(m -1)

c) (TH + VD) Vẽ đồ thị (d’) với giá trị của m tìm được ở câu b.

Câu 15 (1,0 điểm):

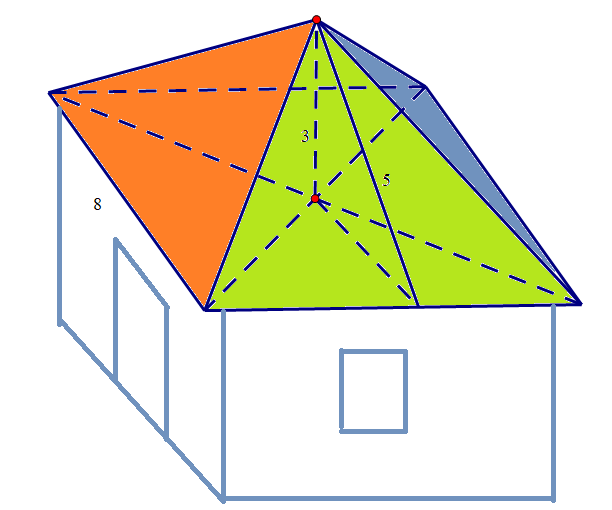
Một mái nhà hình chóp tứ giác đều (hình vẽ) có cạnh đáy là 8 m, chiều cao thuộc mặt bên là 5 m, chiều cao của hình chóp là 3 m. a) (TH) Tính diện tích xung quanh của mái nhà b) (VD) Nếu các mặt bên làm bằng bê tông đổ mái vát, mỗi m2 thành giá là 1 500 000 đồng thì phần mái nhà đó mất tổng bao nhiêu tiền? (Học sinh không phải vẽ lại hình)

Câu 16 (3,0 điểm): Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Gọi AH là đường cao của tam giác ABC.

a) (TH)Chứng minh tam giác ABC vuông tại A

b) (TH)Chứng minh ;

c) (VD)Tính AH và chứng minh AH²= HB.HC.

Câu 17 (0,5 điểm) (VDC): Mẹ Lan mang 400 nghìn đồng đi siêu thị để mua 1kg thịt gà và 2kg thịt lợn, biết giá mỗi kg thịt gà và thịt lợn lần lượt là 140 nghìn đồng và x nghìn đồng.

a) Lập công thức tính số tiền còn lại y ( nghìn đồng) của mẹ Lan sau khi mẹ Lan mua 1 kg thịt gà và 2 kg thịt lợn.

b) Tính giá tiền mỗi kg thịt lợn biết mẹ Lan mua vừa hết số tiền mang theo.

------------------ HẾT ------------------

Đáp án đề thi học kì 2 Toán 8 KNTT Đề 2

Phần I. TRẮC NGHIỆM (3,0 điểm). Mỗi phương án chọn đúng được 0,25 điểm.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	A	B	B	D	C	A	D	C	A	D	C	C

Mời các bạn xem tiếp đáp án phần tự luận trong file tải về.