Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Hoạt động 1 trang 74 Toán 8 Cánh diều tập 2

$\frac{A^{\prime }{B}^{\prime }}{AB};\frac{C^{\prime }{A}^{\prime }}{CA};\frac{B^{\prime }{C}^{\prime }}{BC}$

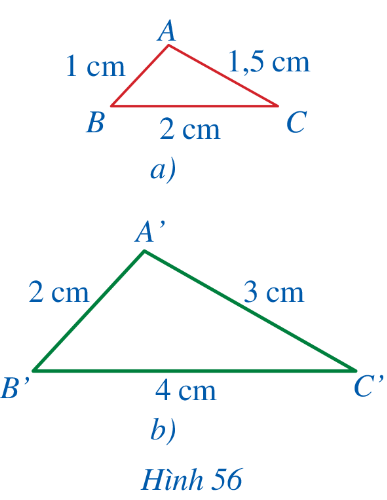
Lời giải chi tiết:

Từ hình vẽ, ta có:

$\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{2}{1}=2$

$\frac{C^{\prime }{A}^{\prime }}{CA}=\frac{3}{1,5}=2$

$\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{4}{2}=2$

Vậy $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{C^{\prime }{A}^{\prime }}{CA}=\frac{B^{\prime }{C}^{\prime }}{BC}$.

Luyện tập 1 trang 75 Toán 8 Cánh diều tập 2

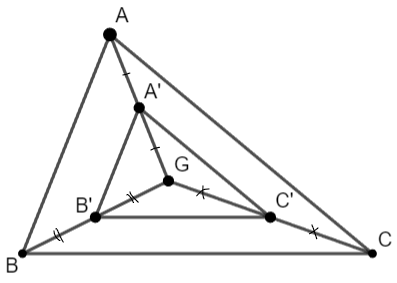
Hướng dẫn giải:

Xét ∆ABG có: GA' = AA' và GB' = BB' nên A'B' là đường trung bình của ∆ABG

Suy ra $A^{\prime }{B}^{\prime }=\frac{1}{2}AB$ hay $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{1}{2}$

Chứng minh tương tự, ta có: A'C' và B'C' lần lượt là đường trung bình của ∆ACG, ∆BCG.

Suy ra $\frac{A^{\prime }{C}^{\prime }}{AC}=\frac{1}{2}$ và $\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{1}{2}$

Xét hai tam giác A'B'C' và ABC có $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{A^{\prime }{C}^{\prime }}{AC}=\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{1}{2}$

Suy ra ∆A’B’C’ ∽ ∆ABC (c . c . c).

Hoạt động 2 trang 76 Toán 8 Cánh diều tập 2

Cho hai tam giác ABC và A'B'C' lần lượt vuông tại A và A' (Hình 60) sao cho AB = 3, BC = 5, A'B' = 6, B'C' = 10.

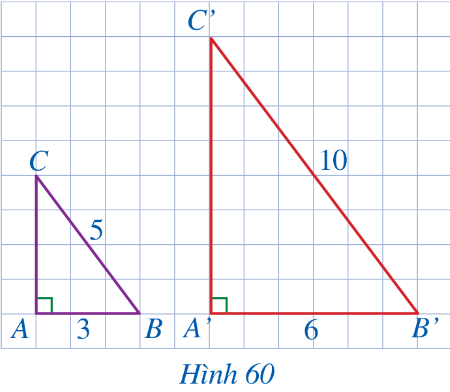
a) Tính CA và C’A’.

b) So sánh các tỉ số $\frac{A^{\prime }{B}^{\prime }}{AB};\frac{B^{\prime }{C}^{\prime }}{BC};\frac{A^{\prime }{C}^{\prime }}{AC}$.

c) Hai tam giác A'B'C' và ABC có đồng dạng với nhau hay không?

Hướng dẫn giải:

a) Xét tam giác ABC vuông tại A có: BC² = AB² + AC² (định lí Pythagore)

Suy ra AC² = BC² - AB² = 5² - 3² = 16.

Vậy AC = 4.

Xét tam giác A'B'C' vuông tại A' có: B'C'² = A'B'² + A'C'² (định lí Pythagore)

Suy ra A'C'² = B'C'² - A'B'² = 10² - 6² = 64.

Vậy A'C' = 8.

b) Ta có: $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{A^{\prime }{C}^{\prime }}{AC}=2$

c) Xét hai tam giác A'B'C' và ABC có $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{A^{\prime }{C}^{\prime }}{AC}=\frac{B^{\prime }{C}^{\prime }}{BC}=2$

Suy ra ∆A’B’C’ ∽ ∆ABC (c . c . c).

Bài 1 trang 78 Toán 8 Cánh diều tập 2

Quan sát Hình 65 và chỉ ra những cặp tam giác đồng dạng:

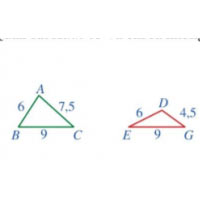
Hướng dẫn giải:

Tam giác ABC đồng dạng với tam giác IKH; tam giác DEG đồng dạng với tam giác MNP.

Bài 2 trang 78 Toán 8 Cánh diều tập 2

Cho hai tam giác ABC và MNP có AB = 2, BC = 5, CA = 6, MN = 4, NP = 10, PM = 12. Hãy viết các cặp góc tương ứng bằng nhau của hai tam giác trên và giải thích kết quả.

Hướng dẫn giải:

Ta có: $\frac{AB}{MN}=\frac{BC}{NP}=\frac{CA}{PM}=\frac{1}{2}$

Suy ra: $\mathrm{△}$ABC $\sim$ $\mathrm{△}$MNP (c.c.c)

Do đó: $\hat{A}=\hat{M}$; $\hat{B}=\hat{N}$; $\hat{C}=\hat{P}$.

Bài 3 trang 78 Toán 8 Cánh diều tập 2

Bác Hùng vẽ bản đồ trong đó dùng ba đỉnh A, B, C của tam giác ABC lần lượt mô tả ba vị trí M, N, P trong thực tiễn. Bác Duy cũng vẽ một bản đồ, trong đó dùng ba đỉnh A', B', C' của tam giác A'B'C' lần lượt mô tả ba vị trí M, N, P đó. Tỉ lệ bản đồ mà bác Hùng và bác Duy vẽ lần lượt là 1 : 1 000 000 và 1 : 500 000. Chứng minh $\mathrm{△}$A'B'C' $\sim$ $\mathrm{△}$ABC và tính tỉ số đồng dạng.

Hướng dẫn giải:

Vì tam giác ABC đồng dạng với tam giác MNP; tam giác A'B'C' đồng dạng với tam giác MNP nên tam giác A'B'C' đồng dạng với tam giác ABC.

Theo giả thuyết ta có: Tam giác ABC đồng dạng với tam giác MNP theo tỉ số $\frac{1}{1000000}$

Nên $\frac{AB}{MN}=\frac{BC}{NP}=\frac{CA}{PM}=\frac{1}{1000000}$

Hay: MN = 1 000 000AB; NP = 1 000 000BC; PM = 1 000 000CA. (1)

Theo giả thuyết ta có: Tam giác A'B'C' đồng dạng với tam giác MNP theo tỉ số $\frac{1}{1500000}$

Nên $\frac{A^{\prime }{B}^{\prime }}{MN}=\frac{B^{\prime }{C}^{\prime }}{NP}=\frac{C^{\prime }{A}^{\prime }}{PM}=\frac{1}{1500000}$

Hay: MN = 1 500 000A'B'; NP = 1 500 000B'C'; PM = 1 500 000C'A'. (2)

Từ (1)(2) ta có: 1 000 000AB = 1 500 000A'B' hay $\frac{A^{\prime }{B}^{\prime }}{AB}=\frac{2}{3}$

1 000 000BC = 1 500 000B'C' hay $\frac{B^{\prime }{C}^{\prime }}{BC}=\frac{2}{3}$

1 000 000CA = 1 500 000C'A' hay $\frac{C^{\prime }{A}^{\prime }}{CA}=\frac{2}{3}$

Vậy tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số $\frac{2}{3}$.

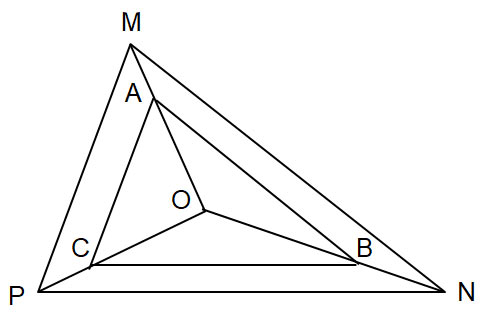
Bài 4 trang 78 Toán 8 Cánh diều tập 2

Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc các tia OA, OB, OC sao cho $\frac{OA}{OM}=\frac{OB}{ON}=\frac{OC}{OP}=\frac{2}{3}$. Chứng minh $\mathrm{△}$ABC $\sim$ $\mathrm{△}$MNP.

Hướng dẫn giải:

Tam giác OMN có: $\frac{OA}{OM}=\frac{OB}{ON}=\frac{2}{3}$

Suy ra: AB // MN nên $\frac{AB}{MN}=\frac{2}{3}$

Chứng minh tương tự ta có: $\frac{BC}{NP}=\frac{2}{3}$; $\frac{CA}{PM}=\frac{2}{3}$

Do đó: $\frac{AB}{MN}=\frac{BC}{NP}=\frac{CA}{PM}$

Vậy $\mathrm{△}$ABC $\sim$ $\mathrm{△}$MNP (c.c.c)

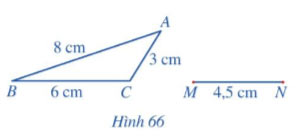
Bài 5 trang 78 Toán 8 Cánh diều tập 2

Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN với các kích thước như Hình 66. Bạn Hoa đố bạn Thanh vẽ điểm P thỏa mãn $\widehat{PMN}=\widehat{ACB}$, $\widehat{PNM}=\widehat{BAC}$ mà không sử dụng thước đo góc. Em hãy giúp bạn Thanh sử dụng thước thẳng (có chia khoảng milimét) và compa để vẽ điểm P và giải thích kết quả tìm được.

Hướng dẫn giải:

Nếu $\widehat{PMN}=\widehat{ACB}$, $\widehat{PNM}=\widehat{BAC}$ thì $\widehat{MPN}=\widehat{CBA}$

Ta có: $\mathrm{△}$ABC $\sim$ $\mathrm{△}$NPM

Do đó: $\frac{AB}{NP}=\frac{BC}{PM}=\frac{CA}{MN}$ hay $\frac{8}{NP}=\frac{6}{PM}=\frac{3}{4,5}$

Ta có: $\frac{8}{NP}=\frac{3}{4,5}$ nên NP = 12 cm.

$\frac{6}{PM}=\frac{3}{4,5}$ nên PM = 9 cm.

Dùng thước kẻ vẽ hai đoạn thẳng NP = 12 cm, PM = 9 cm ta được điểm P thỏa mãn đề bài.

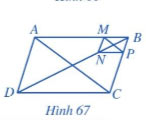
Bài 6 trang 78 Toán 8 Cánh diều tập 2

Cho các hình bình hành ABCD và BMNP như ở Hình 67. Chứng minh:

a) $\frac{BM}{BA}=\frac{BP}{BC}$;

b) $\mathrm{△}$MNP $\sim$ $\mathrm{△}$CBA.

Hướng dẫn giải:

a) Tam giác ABD có MN // AD nên $\frac{BM}{BA}=\frac{BN}{BD}$ (1)

Tam giác BCD có NP // CD nên $\frac{BN}{BD}=\frac{BP}{BC}$ (2)

Từ (1)(2) suy ra: $\frac{BM}{BA}=\frac{BP}{BC}$

b) Từ câu a suy ra MP // AC (định lí Thalès)

Do đó: $\mathrm{△}$PBM $\sim$ $\mathrm{△}$CBA (3)

Ta có: $\frac{PB}{MN}=\frac{BM}{NP}=\frac{MP}{PM}=1$

Suy ra: $\mathrm{△}$PBM $\sim$ $\mathrm{△}$MNP (4)

Từ (3)(4) suy ra: $\mathrm{△}$MNP $\sim$ $\mathrm{△}$CBA.