Toán 8 Kết nối tri thức bài: Luyện tập chung trang 73

Luyện tập chung

4 2.684

VnDoc xin giới thiệu bài Giải Toán 8 Kết nối tri thức bài: Luyện tập chung trang 73 được chúng tôi sưu tầm và giới thiệu với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 8 Kết nối tri thức. Mời các em cùng tham khảo để nắm được nội dung bài học.

Bài: Luyện tập chung trang 73

Bài tập 3.34 trang 73 sgk Toán 8 tập 1 KNTT: Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn MP

a) Hỏi tứ giác AMCP là hình gì? Vì sao?

b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?

Bài giải

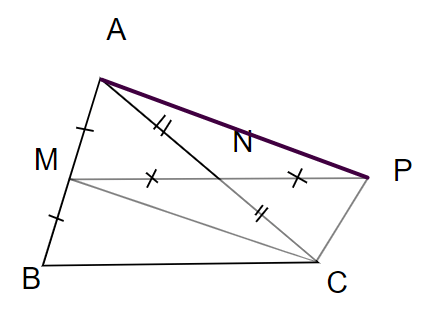
Giải Bài tập 3.34 trang 73 sgk Toán 8 tập 1 Kết nối

a) Xét tứ giác AMCP có NA = NC, NM = NP suy ra AMCP là hình bình hành

b) Để AMCP là hình chữ nhật thì $\widehat{AMC}=90^{\circ}$ suy ra tam giác ABC cân tại C

Để AMCP là hình thoi thì $AC\perp MP mà MN // BC \Rightarrow AC\perp BC$ suy ra tam giác ABC vuông tại C

Để AMCP là hình vuông thì AMCP là hình thoi có 1 góc bằng $90^{\circ}$ suy ra tam giác ABC vuông cân tại C

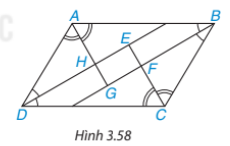
Bài tập 3.35 trang 73 sgk Toán 8 tập 1 KNTT: Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.

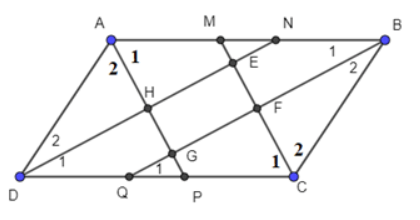
Giải Bài tập 3.35 trang 73 sgk Toán 8 tập 1 Kết nối

Bài giải

Giải Bài tập 3.35 trang 73 sgk Toán 8 tập 1 Kết nối

Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình bình hành.

Ta có: $\widehat{D1}=\widehat{D2}=\frac{\widehat{ADC}}{2}$ (DN là phân giác $\widehat{ADC}$ )

$\widehat{B1}=\widehat{B2}=\frac{\widehat{ABC}}{2}$ (BQ là phân giác $\widehat{ABC}$ )

Mà $\widehat{ABC}=\widehat{ADC}$ (hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{D1}=\widehat{B1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{Q1}=\widehat{B1}$ (hai góc so le trong)

$\Rightarrow \widehat{D1}=\widehat{B1}$

Mà hai góc ở vị trí đồng vị

$\Rightarrow \hat{D_{1}} = \hat{B_{1}}$ DN // BQ hay HE // GF

Ta có: $\widehat{A1}=\widehat{A2}=\frac{\widehat{DAB}}{2}$ (AP là phân giác $\widehat{DAB}$ )

$\widehat{C1}=\widehat{C2}=\frac{\widehat{DCB}}{2}$ (CM là phân giác $\widehat{DCB}$ )

Mà $\widehat{DAB}=\widehat{DCB}$ (hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{A1}=\widehat{C1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{A1}=\widehat{QPG}$ (hai góc so le trong)

$\Rightarrow \widehat{C1}=\widehat{QPG}$

$\Rightarrow \hat{D_{1}} = \hat{B_{1}}$ AP //DM hay GH // EF

Xét tứ giác EFGH có:

HE // GF (cmt)

GH // EF (cmt)

$\Rightarrow \hat{D_{1}} = \hat{B_{1}}$ EFGH là hình bình hành (1)

Xét tam giác BFC, có:

$\widehat{B2}+\widehat{C2}=\frac{\widehat{ABC}}{2}+\frac{\widehat{BCD}}{2}=\frac{\widehat{ABC}+\widehat{BCD}}{2}$

Mà $\widehat{ABC}+\widehat{BCD}=180$ (hai góc trong cùng phía bù nhau)

$\Rightarrow \widehat{B2}+\widehat{C2}=\frac{180^{\circ}}{2}=90^{\circ}$

$\Rightarrow \widehat{BFC}=180^{\circ}-(\widehat{B2}+\widehat{C2})=90^{\circ} hay \Rightarrow \widehat{EFG}=90^{\circ}$

Từ (1) và (2) suy ra tứ giác EFGH là hình chữ nhật.

Bài tập 3.36 trang 73 sgk Toán 8 tập 1 KNTT: Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?

Bài giải

Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình bình hành (do hình bình có 1 góc vuông thì là hình chữ nhật)

Khi nẹp thêm một đường chéo vào khung đó thì nó không còn bị xô lệch do khung đã được cố định bởi đường chéo nẹp thêm

Bài tập 3.37 trang 73 sgk Toán 8 tập 1 KNTT: Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x'Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?

Bài giải

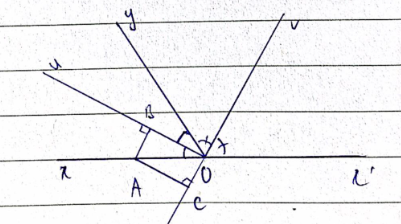
Giải Bài tập 3.37 trang 73 sgk Toán 8 tập 1 Kết nối

Ta có $\widehat{uOv}$ là góc tạo bởi hai đường phân giác của hai góc kề bù $\Rightarrow \widehat{uOv}=90^{\circ}$

Xét tứ giác OBAC ta có: $\widehat{OCA}=\widehat{BOC}=\widehat{OBA}=90^{\circ}$ nên OBAC là hình chữ nhật

Bài tập 3.38 trang 73 sgk Toán 8 tập 1 KNTT: Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN

Bài giải

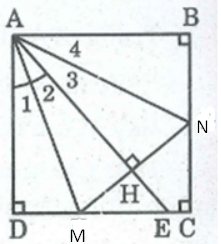
Giải Bài tập 3.38 trang 73 sgk Toán 8 tập 1 Kết nối

Gọi giao điểm của AE và MN là H

Xét tam giác vuông AMD và AMH ta có:

AM chung

$\widehat{A1}=\widehat{A2}$

Suy ra $\Delta AMD=\Delta AMH (ch - gn) \Rightarrow DM=MH, AD=AH$

Xét tam giác vuông ANH và ANB ta có:

AN chung

AH = AB (do cùng = AD)

Suy ra $\Delta ANH=ANB (ch - cgv) \Rightarrow NH = BN$

Ta có $DM = MH, NH = BN \Rightarrow DM+BN=MH+NH=MN$

-------------------------------------

Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài: Luyện tập chung trang 73 KNTT. Trong quá trình học môn Toán lớp 8, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã sưu tầm và chọn lọc thêm phần Đề thi giữa kì 1 lớp 8 hay Đề thi học kì 1 lớp 8 để giúp các bạn học sinh học tốt hơn.

Toán 8 Kết nối tri thức Bài tập cuối chương III

Toán 8 từ năm học 2023 - 2024 trở đi sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Việc lựa chọn giảng dạy bộ sách nào sẽ tùy thuộc vào các trường. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc sẽ cung cấp lời giải bài tập sách giáo khoa, sách bài tập, trắc nghiệm toán từng bài và các tài liệu giảng dạy, học tập khác. Mời các bạn tham khảo qua đường link bên dưới:

Đánh giá bài viết

4 2.684

Bài trước

Bài sau