Toán 8 Luyện tập chung trang 108

Giải Toán 8 Kết nối tri thức tập 2

1 384

Giải Toán 8 Luyện tập chung trang 108 được VnDoc tổng hợp và đăng tải sau đây bao gồm đáp án và hướng dẫn giải chi tiết cho các câu hỏi trong SGK Toán 8 Kết nối tri thức tập 2, giúp các em luyện giải Toán 8 và học tốt môn Toán hơn. Mời các em cùng tham khảo để nắm được nội dung bài học.

Giải Toán 8 KNTT Luyện tập chung trang 108

Bài 9.32 trang 109 Toán 8 KNTT tập 2
Bài 9.33 trang 109 Toán 8 KNTT tập 2
Bài 9.34 trang 109 Toán 8 KNTT tập 2
Bài 9.36 trang 109 Toán 8 KNTT tập 2

Bài 9.32 trang 109 Toán 8 KNTT tập 2

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng $BH=16cm$ , $CH=9cm$

a) Tính độ dài đoạn thẳng AH

b) Tính độ dài đoạn thằng AB và AC

Hướng dẫn giải

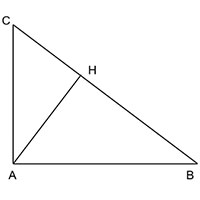
Bài 9.32

a) Có $BC=BH+CH=16+9=25$

Xét tam giác AHC vuông tại H có: $AH^{2}=AC^{2}-CH^{2}$ (định lý Pythagore) (1)

Xét tam giác AHB vuông tại H có: $AH^{2}=AB^{2}-BH^{2}$ (định lý Pythagore) (2)

Xét (1) + (2), có:

$2AH^{2}=AC^{2}-CH^{2}+AB^{2}-BH^{2}$

$2AH^{2}=BC^{2}-CH^{2}-BH^{2}$

$2AH^{2}=25^{2}-9^{2}-16^{2}$

$2AH^{2}=288$

$AH^{2}=144$

$AH=12 (cm)$

b) Có $AC^{2}=AH^{2}+CH^{2}$ (định lý Pythagore)

=> $AC^{2}=12^{2}+9^{2}=225$

=> $AC=15(cm)$

Có $AB^{2}=AH^{2}+BH^{2}$ (định lý Pythagore)

=> $AB^{2}=12^{2}+16^{2}=400$

=> $AB=20(cm)$

Bài 9.33 trang 109 Toán 8 KNTT tập 2

Cho tam giác ABC có $AB=6cm$ , $AC=8cm$ , $BC=10cm$ . Cho điểm M nằm trên cạnh BC sao cho $BM=4cm$ . Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB

Hướng dẫn giải

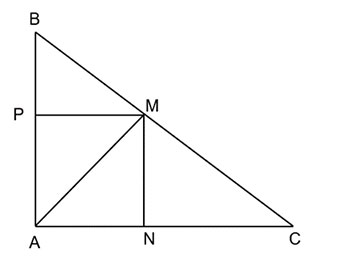
Bài 9.33

a) Ta thấy $AB^{2}+AC^{2}=BC^{2}$

=> Tam giác ABC vuông tại A

Có AC ⊥ AB

mà MP ⊥ AB

=> MP // AC

=> $\widehat{BMP}=\widehat{MCN}$ (2 góc đồng vị)

Xét tam giác vuông BMP (vuông tại P) và tam giác MCN (vuông tại N) có $\widehat{BMP}=\widehat{MCN}$

=> $\Delta BMP$ ~ $\Delta MCN$

b) Xét tam giác BMP và tam giác BAC có MP // AC

=> $\widehat{BPM}=\widehat{BAC}$

=> $\frac{4}{10}=\frac{PM}{8}$

=> $PM=3,2(cm)$

=> $BP=2,4$ (áp dụng định lý Pythagore trong tam giác vuông BMP)

=> $AP=3,6$ (cm)

=> $AM=\sqrt{23.2}$ (áp dụng định lý Pythagore trong tam giác vuông AMP)

Bài 9.34 trang 109 Toán 8 KNTT tập 2

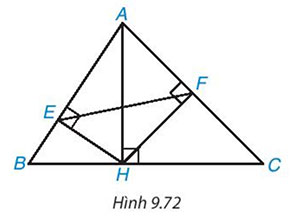
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng

a) $\Delta AEH$ ~ $\Delta AHB$

b) $\Delta AFH$ ~ $\Delta AHC$

c) $\Delta AFE$ ~ $\Delta ABC$

Bài 9.34

Bài 9.36 trang 109 Toán 8 KNTT tập 2

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3m

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3m, hỏi bóng cột cờ dài bao nhiêu mét?

Hướng dẫn giải

a) Gọi x là độ cao của cột đèn, có: $\frac{0,6}{3} = \frac{1,4}{x}$

=> x = 7m

b) Gọi y là độ dài bóng cột cờ, có $\frac{3}{y} = \frac{1,4}{7}$ 3y=1,47

=> y = 15m

-------------------------------------

Ngoài Giải Toán 8 Luyện tập chung trang 108 KNTT tập 2, mời các bạn tham khảo thêm Đề thi giữa kì 2 lớp 8 hay Đề thi học kì 2 lớp 8 để giúp các bạn học sinh học tốt hơn.

Bài tiếp theo: Giải Toán 8 Bài tập cuối chương 9

Đánh giá bài viết

1 384

Bài trước

Bài sau