Giải Toán 8 trang 73 tập 1 Kết nối tri thức
Giải Toán 8 trang 73 Tập 1
Giải Toán 8 trang 73 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 1 trang 73.
Bài 3.34 trang 73 Toán 8 tập 1 Kết nối
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.
a) Hỏi tứ giác AMCP là hình gì? Vì sao?
b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?
Hướng dẫn giải:
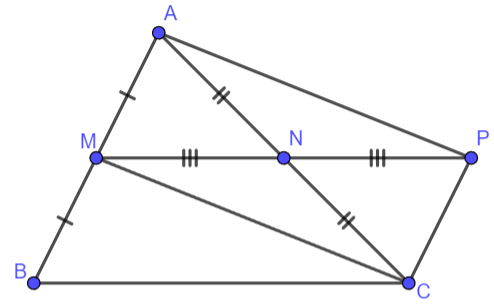
a) Xét tứ giác AMCP có hai đường chéo AC và MP cắt nhau tại trung điểm N mỗi đường
⇒ AMCP là hình bình hành (dhnb)
b) • Để AMCP là hình chữ nhật thì 
\(\widehat{AMC}=90^{\circ}\)
Khi đó đường trung tuyến CM là một đường cao của tam giác ABC
Hay tam giác ABC cân tại C.
• Để AMCP là hình thoi khi và chỉ khi MA = MC
Mà MA = MB (gt)
⇒ Tam giác ABC vuông tại C
• Để AMCP là hình vuông thì MA = MC và \(\widehat{AMC}=90^{\circ}\)
⇒ Tam giác ABC vuông cân tại C.
Bài 3.35 trang 73 Toán 8 tập 1 Kết nối
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.
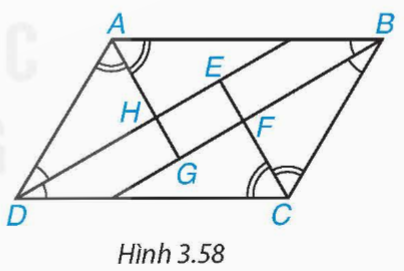
Hướng dẫn giải:
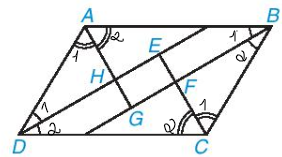
Vì ABCD là hình bình hành nên AB // DC và AD // BC
Do đó \(\widehat{ADC}+\widehat{BCD}=180^{\circ}\)
\(2\widehat{D_2}+2\widehat{C_2}=180^{\circ}\)
\(\widehat{D_2}+\widehat{C_2}=90^{\circ}\) (1)
Xét tam giác EDC có:
\(\widehat{DEC}+\widehat{D_2}+\widehat{C_2}=180^{\circ}\) (định lí tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra \(\widehat{DEC} =90^{\circ}\) hay tam giác EDC vuông tại E
Chứng minh tương tự, ta có ∆ AHD vuông tại H, ∆ GAB vuông tại G
Xét tứ giác HEFG có \(\widehat{HEF}=\widehat{EHG}=\widehat{HGF} =90^{\circ}\)
Suy ra HEFG là hình chữ nhật.
Bài 3.36 trang 73 Toán 8 tập 1 Kết nối
Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?
Hướng dẫn giải:
Khi bị xô lệch, khung tre có dạng hình bình hành vì các cạnh đối bằng nhau.
Nếu nẹp thêm một thanh đường chéo thì khung không còn bị xô lệch vì nó được cố định bởi thanh đường chéo và bốn thanh của khung.
Bài 3.37 trang 73 Toán 8 tập 1 Kết nối
Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x'Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
Hướng dẫn giải:
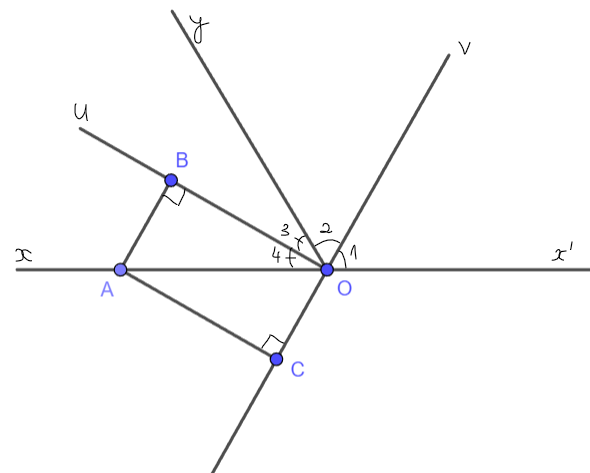
Ta có \(\widehat{xOy} +\widehat{x'Oy}=180^{\circ}\) (hai góc kề bù)
\(2\widehat{O_3} +2\widehat{O_2}=180^{\circ}\)
\(\widehat{O_3} +\widehat{O_2}=90^{\circ}\)
⇒ \(\widehat{uOv} =90^{\circ}\) hay \(\widehat{BOC} =90^{\circ}\)
Xét tứ giác ABOC có \(\widehat{ABO} =\widehat{BOC} =\widehat{OCA} =90^{\circ}\)
⇒ ABOC là hình chữ nhật.
Bài 3.38 trang 73 Toán 8 tập 1 Kết nối
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN
Hướng dẫn giải:
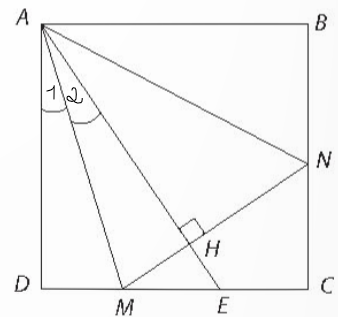
Xét tam giác ADM và tam giác AHM có:
\(\widehat{ADM} =\widehat{AHM}=90^{\circ}\)
\(\widehat{A_1} =\widehat{A_2}\) (gt)
AM chung
Do đó, ∆ ADM = ∆ AHM (ch – gn)
⇒ AD = AH và MD = MH (các cạnh tương ứng)
Xét tam giác AHN và tam giác ABN có:
\(\widehat{AHN} =\widehat{ABN}=90^{\circ}\)
AH = AB ( = AD)
AN chung
Do đó, ∆ AHN = ∆ ABN (ch – cgv)
Suy ra HN = BN (hai cạnh tương ứng)
Vậy DM + BN = MH + HN = MN (đpcm)
-----------------------------------------------
Lời giải Toán 8 trang 73 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức bài: Luyện tập chung trang 73, được VnDoc biên soạn và đăng tải!
