Toán 8 Kết nối tri thức Bài tập cuối chương 2

Sách Kết nối tri thức

Giải Toán 8: Bài tập cuối chương II hướng dẫn giải bài tập trong SGK Toán 8 Kết nối tri thức trang 47 tập 1, giúp các em nắm vững kiến thức được học trong bài và luyện giải Toán 8 hiệu quả. Mời các em cùng tham khảo để nắm được nội dung bài học.

A. Trắc nghiệm

Bài tập 2.28 trang 47 sgk Toán 8 tập 1 KNTT:

Đa thức $x^{2}-9x+8$ $x^{2} - 9 x + 8$ được phân tích thành tích của hai đa thức

A. x - 1 và x + 8

B. x - 1 và x - 8

C. x - 2 và x - 4

C. x - 2 và x + 4

Hướng dẫn giải:

$x^{2}-9x+8=(x^{2}-9x+9)-1=(x-3)^{2}-1^{2}$ $x^{2} - 9 x + 8 = (x^{2} - 9 x + 9) - 1 = (x - 3)^{2} - 1^{2}$

$= (x - 3 - 1) (x - 3 + 1) = (x - 4) (x - 2)$

Đáp án: C

Bài tập 2.29 trang 47 sgk Toán 8 tập 1 KNTT:

Khẳng định nào sau đây là đúng?

A. $(A-B)(A+B)=A^{2}+2AB+B^{2}$ $(A - B) (A + B) = A^{2} + 2 A B + B^{2}$

B. $(A+B)(A-B)=A^{2}-2AB+B^{2}$ $(A + B) (A - B) = A^{2} - 2 A B + B^{2}$

C. $(A+B)(A-B)=A^{2}+B^{2}$ $(A + B) (A - B) = A^{2} + B^{2}$

D. $(A+B)(A-B)=A^{2}-B^{2}$ $(A + B) (A - B) = A^{2} - B^{2}$

Hướng dẫn giải:

Đáp án: D

Bài tập 2.30 trang 47 sgk Toán 8 tập 1 KNTT:

Biểu thức $25x^{2}+20xy+4y^{2}$ $25 x^{2} + 20 x y + 4 y^{2}$ viết dưới dạng bình phương của một tổng là:

A. $[5x+(-2y)]^{2}$ $[5 x + (- 2 y)]^{2}$

B. $[2x+(-5y)]^{2}$ $[2 x + (- 5 y)]^{2}$

C. $(2x+5y)^{2}$ $(2 x + 5 y)^{2}$

D. $(5x+2y)^{2}$ $(5 x + 2 y)^{2}$

Hướng dẫn giải:

Đáp án: D

Bài tập 2.31 trang 47 sgk Toán 8 tập 1 KNTT:

Rút gọn biểu thức $A=(2x+1)^{3}-6x(2x+1)$ $A = (2 x + 1)^{3} - 6 x (2 x + 1)$ ta được

A. $x^{3}+8$ $x^{3} + 8$

B. $x^{3}+1$ $x^{3} + 1$

C. $8x^{3}+1$ $8 x^{3} + 1$

D. $8x^{3}-1$ $8 x^{3} - 1$

Hướng dẫn giải:

$A=(2x+1)^{3}-6x(2x+1)=(2x+1)(4x^{2}+4x+1-6x)$ $A = (2 x + 1)^{3} - 6 x (2 x + 1) = (2 x + 1) (4 x^{2} + 4 x + 1 - 6 x)$

$=(2x+1)(4x^{2}-2x+1)$ $= (2 x + 1) (4 x^{2} - 2 x + 1)$

$=8x^{3}-4x^{2}+2x+4x^{2}-2x+1=8x^{3}+1$ $= 8 x^{3} - 4 x^{2} + 2 x + 4 x^{2} - 2 x + 1 = 8 x^{3} + 1$

Đáp án: C

B. Tự luận

Bài tập 2.32 trang 47 sgk Toán 8 tập 1 KNTT:

Tính nhanh giá trị của các biểu thức:

a) $x^{2}-4x+4$ $x^{2} - 4 x + 4$ tại x = 102

b) $x^{3}+3x^{2}+3x+1$ $x^{3} + 3 x^{2} + 3 x + 1$ tại x = 999

Hướng dẫn giải:

a) $x^{2}-4x+4=(x-2)^{2}$ $x^{2} - 4 x + 4 = (x - 2)^{2}$

$=(102-2)^{2}=100^{2}=10000$ $= (102 - 2)^{2} = 100^{2} = 10000$

b) $x^{3}+3x^{2}+3x+1=(x+1)^{3}$ $x^{3} + 3 x^{2} + 3 x + 1 = (x + 1)^{3}$

$=(999+1)^{3}=1000^{3}=1000000$ $= (999 + 1)^{3} = 1000^{3} = 1000000$

Bài tập 2.33 trang 47 sgk Toán 8 tập 1 KNTT:

Rút gọn các biểu thức:

a) $(2x-5y)(2x+5y)+(2x+5y)^{2}$ $(2 x - 5 y) (2 x + 5 y) + (2 x + 5 y)^{2}$

b) $(x+2y)(x^{2}-2xy+4y^{2})+(2x-y)(4x^{2}+x2y+y^{2})$ $(x + 2 y) (x^{2} - 2 x y + 4 y^{2}) + (2 x - y) (4 x^{2} + x 2 y + y^{2})$

Hướng dẫn giải:

a) $(2x-5y)(2x+5y)+(2x+5y)^{2}$ $(2 x - 5 y) (2 x + 5 y) + (2 x + 5 y)^{2}$

$=4x^{2}-25y^{2}+4x^{2}+20xy+25y^{2}$ $= 4 x^{2} - 25 y^{2} + 4 x^{2} + 20 x y + 25 y^{2}$

$=8x^{2}+20xy$ $= 8 x^{2} + 20 x y$

b) $(x+2y)(x^{2}-2xy+4y^{2})+(2x-y)(4x^{2}+x2y+y^{2})$ $(x + 2 y) (x^{2} - 2 x y + 4 y^{2}) + (2 x - y) (4 x^{2} + x 2 y + y^{2})$

$=x^{3}+8y^{3}+8x^{3}-y^{3}=9x^{3}+7y^{3}$ $= x^{3} + 8 y^{3} + 8 x^{3} - y^{3} = 9 x^{3} + 7 y^{3}$

Bài tập 2.34 trang 47 sgk Toán 8 tập 1 KNTT:

Phân tích các đa thức sau thành nhân tử:

a) $6x^{2}-24y^{2}$ $6 x^{2} - 24 y^{2}$

b) $64x^{3}-27y^{3}$ $64 x^{3} - 27 y^{3}$

c) $x^{4}-2x^{3}+x^{2}$ $x^{4} - 2 x^{3} + x^{2}$

d) $(x-y)^{3}+8y^{3}$ $(x - y)^{3} + 8 y^{3}$

Hướng dẫn giải:

a) $6x^{2}-24y^{2}=6(x^{2}-4y^{2})$ $6 x^{2} - 24 y^{2} = 6 (x^{2} - 4 y^{2})$

$= 6 (x - 2 y) (x + 2 y)$

b) $64x^{3}-27y^{3}=(4x-3y)(16x^{2}+12xy+9y^{2})$ $64 x^{3} - 27 y^{3} = (4 x - 3 y) (16 x^{2} + 12 x y + 9 y^{2})$

c) $x^{4}-2x^{3}+x^{2}=x^{2}(x^{2}-2x+1)$ $x^{4} - 2 x^{3} + x^{2} = x^{2} (x^{2} - 2 x + 1)$

$=x^{2}(x-1)^{2}$ $= x^{2} (x - 1)^{2}$

d) $(x-y)^{3}+8y^{3}=(x-y+2y)[x^{2}-2xy+y^{2}-2y(x-y)+4y^{2}]$ $(x - y)^{3} + 8 y^{3} = (x - y + 2 y) [x^{2} - 2 x y + y^{2} - 2 y (x - y) + 4 y^{2}]$

$=(x+y)(x^{2}-2xy+y^{2}-2xy+2y^{2}+4y^{2})$ $= (x + y) (x^{2} - 2 x y + y^{2} - 2 x y + 2 y^{2} + 4 y^{2})$

$=(x+y)(x^{2}-4xy+7y^{2})$ $= (x + y) (x^{2} - 4 x y + 7 y^{2})$

Bài tập 2.35 trang 47 sgk Toán 8 tập 1 KNTT:

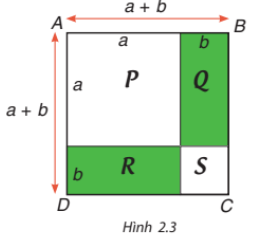
Sử dụng Hình 2.3. bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức $(a+b)^{2}=a^{2}+2ab+b^{2}$ $(a + b)^{2} = a^{2} + 2 a b + b^{2}$

Giải Bài tập 2.35 trang 47 sgk Toán 8 tập 1 Kết nối

Hướng dẫn giải:

Cách 1: Diện tích hình vuông ABCD là: $(a+b)(a+b)=(a+b)^{2}$ $(a + b) (a + b) = (a + b)^{2}$

Cách 2: Diện tích hình vuông ABCD là:

$P + Q + R + S = a^{2}+ ab+ba+b^{2}$ $P + Q + R + S = a^{2} + a b + b a + b^{2}$

$=a^{2}+2ab+b^{2}$ $= a^{2} + 2 a b + b^{2}$

Từ đó, ta có thể giải thích được hằng đẳng thức $(a+b)^{2}=a^{2}+2ab+b^{2}$ $(a + b)^{2} = a^{2} + 2 a b + b^{2}$

Chia sẻ, đánh giá bài viết

5

4.074

Bài trước

Bài sau

Chia sẻ bởi:
1m52

Tải về

Chọn file muốn tải về:

Toán 8 Kết nối tri thức Bài tập cuối chương 2

204,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!