Giải Toán 8 trang 83 tập 2 Kết nối tri thức
Giải Toán 8 trang 83 Tập 2
Giải Toán 8 trang 83 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 83.
Hoạt động 1 trang 83 Toán 8 tập 2 Kết nối
Cho hai tam giác ABC và A'B'C' có ![]() \(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\).
\(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\).
a) Nếu A'B' = AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
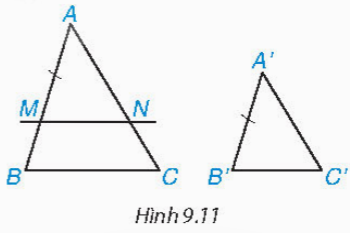
b) Nếu A′B' < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN = A’C’, MN = B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Hướng dẫn giải:
a) Ta có ![]() \(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\) và A'B' = AB
\(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\) và A'B' = AB
⇒ A'C' = AC và B'C' = BC
Khi đó ![]() \(\widehat{A'} =\widehat{A},\ \widehat{B'}=\widehat{B}', \ \widehat{C'}=\widehat{C}\)
\(\widehat{A'} =\widehat{A},\ \widehat{B'}=\widehat{B}', \ \widehat{C'}=\widehat{C}\)
Vậy nếu A'B' = AB thì hai tam giác có đồng dạng với nhau.
b) Ta có MN // BC (M ∈ AB; N ∈ AC)
⇒ Δ AMN ∽ Δ ABC (định lí)
⇒ ![]() \(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)
Mặt khác ta có: ![]() \(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\) và AM = A'B'
\(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}\) và AM = A'B'
⇒ AN = A'C'; AM = A'B'.
Ta có: Δ AMN ∽ Δ ABC
Δ AMN = Δ A'B'C' (c.c.c)
⇒ Δ A'B'C' ∽ Δ ABC.
c) Nếu A'B' > AB, ta đổi vai trò Δ ABC và Δ A'B'C' cho nhau thì Δ ABC ∽ Δ A'B'C'.
-----------------------------------------------
Lời giải Toán 8 trang 83 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 34: Ba trường hợp đồng dạng của hai tam giác, được VnDoc biên soạn và đăng tải!








