Giải Toán 8 trang 85 tập 2 Kết nối tri thức
Giải Toán 8 trang 85 Tập 2
Giải Toán 8 trang 85 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 85.
Luyện tập 1 trang 85 Toán 8 tập 2 Kết nối
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27 cm. Biết rằng AB = 4 cm, BC = 6 cm, DE = 6 cm, FD = 12 cm.
Chứng minh Δ ABC ∽ Δ DEF.
Hướng dẫn giải:
Ta có AC = 18 - 4 - 6 = 8 cm
EF = 27 - 6 - 12 = 9 cm
Xét Δ ABC và Δ DEF có 
\(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF} =\frac{2}{3}\)
Suy ra Δ ABC ∽ Δ DEF (đpcm).
Vận dụng trang 85 Toán 8 tập 2 Kết nối
Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.
Tính huống: Trong môn bóng đá, độ khó của mỗi pha ghi bàn còn được tính bởi góc sút vào cầu môn là rộng hay hẹp. Nếu biết độ rộng của khung thành là 7,32 m, trái bóng cách hai cột gôn lần lượt là 10,98 m và 14,64 m thì em có cách nào để đo được góc sút ở vị trí này bởi các dụng cụ học tập không?
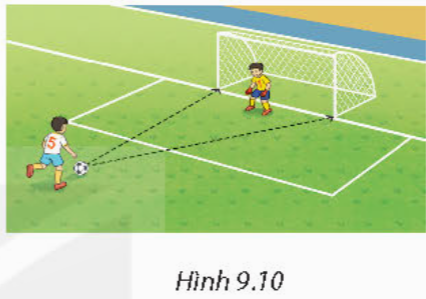
Hướng dẫn giải:
Ta vẽ tam giác ABC với AB = 2 cm, BC = 3 cm và AC = 4 cm.
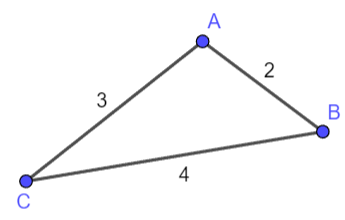
Do tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn nên hai tam giác đồng dạng với nhau.
Khi đó góc sút vào cầu môn bằng góc C của tam giác ABC.
Vậy \(\widehat{C} ≈29^{\circ}\).
Hoạt động 2 trang 85 Toán 8 tập 2 Kết nối
Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng \(\widehat{A} =\widehat{A'} =60^{\circ}\).
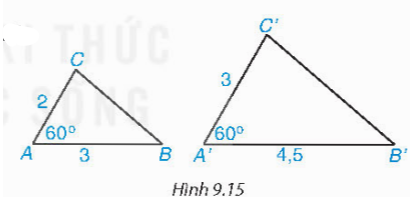
• So sánh các tỉ số \(\frac{A'B'}{AB},\ \frac{A'C'}{AC}\)
• Dùng thước có vạch chia đo độ dài BC, B'C' và tính tỉ số \(\frac{B'C'}{BC}\)
• Theo em, tam giác A'B'C' có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Hướng dẫn giải:
Ta có: \(\frac{A'B'}{AB}= \frac{A'C'}{AC} =\frac{3}{2}\)
Sử dụng thước đo độ dài ta được BC ≈ 2,6 cm và B'C' ≈ 3,9 cm. Do đó \(\frac{B'C'}{BC} =\frac{3}{2}\)
Vậy Δ A'B'C' ∽ Δ ABC (c.c.c)
⇒ tỉ số đồng dạng là \(k=\frac{3}{2}\).
-----------------------------------------------
Lời giải Toán 8 trang 85 Tập 2 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 8 Kết nối tri thức Bài 34: Ba trường hợp đồng dạng của hai tam giác, được VnDoc biên soạn và đăng tải!
