Giải Toán 8 bài 5: Phương trình chứa ẩn ở mẫu
Giải bài tập Toán 8 bài 5: Phương trình chứa ẩn ở mẫu
Giải bài tập SGK Toán lớp 8 bài 5: Phương trình chứa ẩn ở mẫu với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo
- Giải bài tập SGK Toán lớp 8 bài 2: Phương trình bậc nhất một ẩn và cách giải
- Giải bài tập SGK Toán lớp 8 bài 3: Phương trình đưa được về dạng ax + b = 0
- Giải bài tập SGK Toán lớp 8 bài 4: Phương trình tích
Trả lời câu hỏi Toán 8 Tập 2 Bài 5
Trả lời câu hỏi Toán 8 Tập 2 Bài 5 trang 19:
Giá trị x = 1 có phải là nghiệm của phương trình hay không? Vì sao?
Lời giải
Giá trị x = 1 không phải là nghiệm của phương trình.
Vì tại x = 1 thì ![]() \(\frac{1}{x-1}\) có mẫu bằng 0, vô lí
\(\frac{1}{x-1}\) có mẫu bằng 0, vô lí
Trả lời câu hỏi Toán 8 Tập 2 Bài 5 trang 20:
Tìm điều kiện xác định của mỗi phương trình sau:
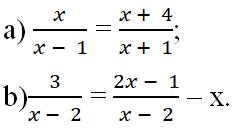
Lời giải
a) x – 1 ≠ 0 khi x ≠ 1 và x + 2 ≠ 0 khi x ≠ - 2
Vậy ĐKXĐ của phương trình ![]() là x ≠ 1 và x ≠ - 2
là x ≠ 1 và x ≠ - 2
b) x – 2 ≠ 0 khi x ≠ 2
Vậy ĐKXĐ của phương trình ![]() là x ≠ 2
là x ≠ 2
Trả lời câu hỏi Toán 8 Tập 2 Bài 5 trang 22:
Giải các phương trình trong câu hỏi 2
Lời giải
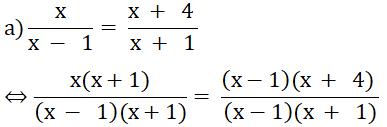
Suy ra x(x + 1) = (x - 1)(x + 4)
Ta có:
x(x + 1) = (x - 1)(x + 4)
⇔ x2 + x = x2 + 4x - x - 4
⇔ x = 3x - 4
⇔ 2x = 4
⇔ x = 2 (thỏa mãn ĐKXĐ)
Vậy tập nghiệm của phương trình là: S = {2}
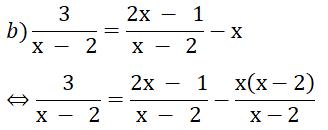
Suy ra 3 = 2x - 1 - x(x - 2)
⇔ 3 = 2x - 1-(x2 - 2x)
⇔ 3 = 2x - 1 - x2 + 2x
⇔ 3 = - 1 - x2
⇔ x2 = -4 (vô nghiệm)
Vậy tập nghiệm của phương trình là: S = ∅
Giải bài tập toán 8 trang 22 tập 2
Bài 27 (trang 22 SGK Toán 8 Tập 2)
Giải các phương trình:
a) ![]() \(\dfrac{2x-5}{x+5}= 3\)
\(\dfrac{2x-5}{x+5}= 3\)
c) ![]() \(\dfrac{(x^{2}+2x)-(3x+6)}{x-3}=0\)
\(\dfrac{(x^{2}+2x)-(3x+6)}{x-3}=0\)
b) ![]() \(\dfrac{x^{2}-6}{x}=x+\dfrac{3}{2}\)
\(\dfrac{x^{2}-6}{x}=x+\dfrac{3}{2}\)
d) ![]() \(\dfrac{5}{3x+2}= 2x-1\)
\(\dfrac{5}{3x+2}= 2x-1\)
 \(\eqalign{
& {{2x - 5} \over {x + 5}} = 3 \cr
& \Leftrightarrow {{2x - 5} \over {x + 5}} = {{3(x + 5)} \over {x + 5}} \cr
& \Rightarrow 2x - 5 = 3\left( {x + 5} \right) \cr
& \Leftrightarrow 2x - 5 = 3x + 15 \cr
& \Leftrightarrow 2x - 3x = 15 + 5 \cr
& \Leftrightarrow - x = 20 \cr
& \Leftrightarrow x = - 20 \text{ (thỏa mãn ĐKXĐ)}\cr}\)
\(\eqalign{
& {{2x - 5} \over {x + 5}} = 3 \cr
& \Leftrightarrow {{2x - 5} \over {x + 5}} = {{3(x + 5)} \over {x + 5}} \cr
& \Rightarrow 2x - 5 = 3\left( {x + 5} \right) \cr
& \Leftrightarrow 2x - 5 = 3x + 15 \cr
& \Leftrightarrow 2x - 3x = 15 + 5 \cr
& \Leftrightarrow - x = 20 \cr
& \Leftrightarrow x = - 20 \text{ (thỏa mãn ĐKXĐ)}\cr}\)
Vậy tập nghiệm của phương trình là: ![]() \(S = \{-20\}\)
\(S = \{-20\}\)
b) ĐKXĐ: ![]() \(x \ne 0\)
\(x \ne 0\)
 \(\eqalign{
& {{{x^2} - 6} \over x} = x + {3 \over 2} \cr
& \Leftrightarrow {{2({x^2} - 6)} \over {2x}} = {{2{x^2}} \over {2x}} + {{3x} \over {2x}} \cr
& \Rightarrow 2\left( {{x^2} - 6} \right) = 2{x^2} + 3x \cr
& \Leftrightarrow 2{x^2} - 12 = 2{x^2} + 3x \cr
& \Leftrightarrow 2{x^2} - 2{x^2} - 3x = 12 \cr
& \Leftrightarrow - 3x = 12 \cr
& \Leftrightarrow x = 12:\left( { - 3} \right) \cr
& \Leftrightarrow x = - 4\text{ (thỏa mãn ĐKXĐ)} \cr}\)
\(\eqalign{
& {{{x^2} - 6} \over x} = x + {3 \over 2} \cr
& \Leftrightarrow {{2({x^2} - 6)} \over {2x}} = {{2{x^2}} \over {2x}} + {{3x} \over {2x}} \cr
& \Rightarrow 2\left( {{x^2} - 6} \right) = 2{x^2} + 3x \cr
& \Leftrightarrow 2{x^2} - 12 = 2{x^2} + 3x \cr
& \Leftrightarrow 2{x^2} - 2{x^2} - 3x = 12 \cr
& \Leftrightarrow - 3x = 12 \cr
& \Leftrightarrow x = 12:\left( { - 3} \right) \cr
& \Leftrightarrow x = - 4\text{ (thỏa mãn ĐKXĐ)} \cr}\)
Vậy tập nghiệm của phương trình là: ![]() \(S = \{- 4\}\).
\(S = \{- 4\}\).
c) ĐKXĐ: ![]() \(x \ne 3\)
\(x \ne 3\)
 \(\eqalign{
& {{({x^2} + 2x) - (3x + 6)} \over {x - 3}} = 0 \cr
& \Rightarrow ({x^2} + 2x) - (3x + 6) = 0 \cr
& \Leftrightarrow x\left( {x + 2} \right) - 3\left( {x + 2} \right) = 0 \cr
& \Leftrightarrow \left( {x + 2} \right)\left( {x - 3} \right) = 0 \cr
& \Leftrightarrow \left[ \matrix{
x + 2 = 0 \hfill \cr
x - 3 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = - 2\text{ (thỏa mãn ĐKXĐ)} \hfill \cr
x = 3 \text{ (loại)}\hfill \cr} \right. \cr}\)
\(\eqalign{
& {{({x^2} + 2x) - (3x + 6)} \over {x - 3}} = 0 \cr
& \Rightarrow ({x^2} + 2x) - (3x + 6) = 0 \cr
& \Leftrightarrow x\left( {x + 2} \right) - 3\left( {x + 2} \right) = 0 \cr
& \Leftrightarrow \left( {x + 2} \right)\left( {x - 3} \right) = 0 \cr
& \Leftrightarrow \left[ \matrix{
x + 2 = 0 \hfill \cr
x - 3 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = - 2\text{ (thỏa mãn ĐKXĐ)} \hfill \cr
x = 3 \text{ (loại)}\hfill \cr} \right. \cr}\)
Vậy tập nghiệm của phương trình là: ![]() \(S = \{-2\}\)
\(S = \{-2\}\)
d) ĐKXĐ: ![]() \(x \ne -\dfrac{2}{3}\)
\(x \ne -\dfrac{2}{3}\)
 \(\eqalign{
& {5 \over {3x + 2}} = 2x - 1 \cr
& \Leftrightarrow {5 \over {3x + 2}} = {{\left( {2x - 1} \right)\left( {3x + 2} \right)} \over {3x + 2}} \cr
& \Rightarrow 5 = \left( {2x - 1} \right)\left( {3x + 2} \right) \cr
& \Leftrightarrow 5 = 6{x^2} + 4x - 3x - 2 \cr
& \Leftrightarrow 5 = 6{x^2} + x - 2 \cr
& \Leftrightarrow - 6{x^2} - x + 2 + 5 = 0 \cr
& \Leftrightarrow - 6{x^2} - x + 7 = 0 \cr
& \Leftrightarrow - 6{x^2} + 6x - 7x + 7 = 0 \cr
& \Leftrightarrow - 6x\left( {x - 1} \right) - 7\left( {x - 1} \right) = 0 \cr
& \Leftrightarrow \left( {x - 1} \right)\left( { - 6x - 7} \right) = 0 \cr
& \Leftrightarrow \left[ \matrix{
x - 1 = 0 \hfill \cr
- 6x - 7 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
- 6x = 7 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = 1\text{ (thỏa mãn)} \hfill \cr
x = - \dfrac{7}{6}\text{ (thỏa mãn)} \hfill \cr} \right. \cr}\)
\(\eqalign{
& {5 \over {3x + 2}} = 2x - 1 \cr
& \Leftrightarrow {5 \over {3x + 2}} = {{\left( {2x - 1} \right)\left( {3x + 2} \right)} \over {3x + 2}} \cr
& \Rightarrow 5 = \left( {2x - 1} \right)\left( {3x + 2} \right) \cr
& \Leftrightarrow 5 = 6{x^2} + 4x - 3x - 2 \cr
& \Leftrightarrow 5 = 6{x^2} + x - 2 \cr
& \Leftrightarrow - 6{x^2} - x + 2 + 5 = 0 \cr
& \Leftrightarrow - 6{x^2} - x + 7 = 0 \cr
& \Leftrightarrow - 6{x^2} + 6x - 7x + 7 = 0 \cr
& \Leftrightarrow - 6x\left( {x - 1} \right) - 7\left( {x - 1} \right) = 0 \cr
& \Leftrightarrow \left( {x - 1} \right)\left( { - 6x - 7} \right) = 0 \cr
& \Leftrightarrow \left[ \matrix{
x - 1 = 0 \hfill \cr
- 6x - 7 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
- 6x = 7 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = 1\text{ (thỏa mãn)} \hfill \cr
x = - \dfrac{7}{6}\text{ (thỏa mãn)} \hfill \cr} \right. \cr}\)
Vậy tập nghiệm của phương trình là: ![]() \(S = \left\{ {1; - \dfrac{7}{6}} \right\}\).
\(S = \left\{ {1; - \dfrac{7}{6}} \right\}\).
Bài 28 (trang 22 SGK Toán 8 Tập 2)
Giải các phương trình:
a) ![]() \(\dfrac{2x-1}{x-1}+1=\dfrac{1}{x-1}\)
\(\dfrac{2x-1}{x-1}+1=\dfrac{1}{x-1}\)
c) ![]() \(x+\frac{1}{x}=x^2+\frac{1}{x^2}\)
\(x+\frac{1}{x}=x^2+\frac{1}{x^2}\)
b) ![]() \(\dfrac{5x}{2x+2}+1=-\dfrac{6}{x+1}\)
\(\dfrac{5x}{2x+2}+1=-\dfrac{6}{x+1}\)
d) ![]() \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x} = 2\)
\(\dfrac{x+3}{x+1}+\dfrac{x-2}{x} = 2\)
 \(\begin{array}{*{20}{l}}
{\dfrac{{2{\rm{x}} - 1}}{{x - 1}} + 1 = \dfrac{1}{{x - 1}}}\\
\begin{array}{l}
\Leftrightarrow \dfrac{{2{\rm{x}} - 1}}{{x - 1}} + \dfrac{{x - 1}}{{x - 1}} = \dfrac{1}{{x - 1}}\\
\Rightarrow 2x - 1 + x - 1 = 1
\end{array}\\
\begin{array}{l}
\Leftrightarrow 3{\rm{x}} - 2 = 1\\
\Leftrightarrow 3x = 1 + 2
\end{array}\\
{ \Leftrightarrow 3{\rm{x}} = 3}\\
{ \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }}{\kern 1pt} {\rm{3:3}}}\\
{ \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }}{\kern 1pt} 1\left( \text{loại} \right)}
\end{array}\)
\(\begin{array}{*{20}{l}}
{\dfrac{{2{\rm{x}} - 1}}{{x - 1}} + 1 = \dfrac{1}{{x - 1}}}\\
\begin{array}{l}
\Leftrightarrow \dfrac{{2{\rm{x}} - 1}}{{x - 1}} + \dfrac{{x - 1}}{{x - 1}} = \dfrac{1}{{x - 1}}\\
\Rightarrow 2x - 1 + x - 1 = 1
\end{array}\\
\begin{array}{l}
\Leftrightarrow 3{\rm{x}} - 2 = 1\\
\Leftrightarrow 3x = 1 + 2
\end{array}\\
{ \Leftrightarrow 3{\rm{x}} = 3}\\
{ \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }}{\kern 1pt} {\rm{3:3}}}\\
{ \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }}{\kern 1pt} 1\left( \text{loại} \right)}
\end{array}\)
Vậy phương trình vô nghiệm.
b) ĐKXĐ: ![]() \(x \ne -1\)
\(x \ne -1\)
 \(\matrix{\dfrac{{5{\text{x}}}}{{2{\text{x}} + 2}} + 1 = - \dfrac{6}{{x + 1}} \hfill \cr { \Leftrightarrow \dfrac{{5{\text{x}}}}{{2\left( {{\text{x}} + 1} \right)}} + 1 = - \dfrac{6}{{x + 1}}} \hfill \cr \matrix{ \Leftrightarrow \dfrac{{5{\text{x}}}}{{2\left( {{\text{x}} + 1} \right)}} + \dfrac{{2x + 2}}{{2\left( {x + 1} \right)}} = - \dfrac{{6.2}}{{2\left( {x + 1} \right)}} \hfill \cr \Rightarrow 5x + 2x + 2 = - 12 \hfill \cr} \hfill \cr { \Leftrightarrow 7{\rm{x}} + 2 = - 12} \hfill \cr { \Leftrightarrow 7{\rm{x}} = - 12 - 2} \hfill \cr { \Leftrightarrow 7{\rm{x}} = - 14} \hfill \cr { \Leftrightarrow x = \left( { - 14} \right):7} \hfill \cr { \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }} - 2\left( \text{thỏa mãn} \right)} \hfill \cr }\)
\(\matrix{\dfrac{{5{\text{x}}}}{{2{\text{x}} + 2}} + 1 = - \dfrac{6}{{x + 1}} \hfill \cr { \Leftrightarrow \dfrac{{5{\text{x}}}}{{2\left( {{\text{x}} + 1} \right)}} + 1 = - \dfrac{6}{{x + 1}}} \hfill \cr \matrix{ \Leftrightarrow \dfrac{{5{\text{x}}}}{{2\left( {{\text{x}} + 1} \right)}} + \dfrac{{2x + 2}}{{2\left( {x + 1} \right)}} = - \dfrac{{6.2}}{{2\left( {x + 1} \right)}} \hfill \cr \Rightarrow 5x + 2x + 2 = - 12 \hfill \cr} \hfill \cr { \Leftrightarrow 7{\rm{x}} + 2 = - 12} \hfill \cr { \Leftrightarrow 7{\rm{x}} = - 12 - 2} \hfill \cr { \Leftrightarrow 7{\rm{x}} = - 14} \hfill \cr { \Leftrightarrow x = \left( { - 14} \right):7} \hfill \cr { \Leftrightarrow {\rm{x}}{\kern 1pt} {\rm{ = }} - 2\left( \text{thỏa mãn} \right)} \hfill \cr }\)
Vậy phương trình có nghiệm x = -2.
c) ĐKXĐ: ![]() \(x \ne 0\).
\(x \ne 0\).
 \(\begin{array}{l}
x + \dfrac{1}{x} = {x^2} + \dfrac{1}{{{x^2}}}\\ \Leftrightarrow \dfrac{{{x^3}}}{{{x^2}}} + \dfrac{x}{{{x^2}}} = \dfrac{{{x^4}}}{{{x^2}}} + \dfrac{1}{{{x^2}}}\\
\Rightarrow {x^3} + x = {x^4} + 1\\
\Leftrightarrow {x^4} - {x^3} - x + 1 = 0\\
\Leftrightarrow {x^3}\left( {x - 1} \right) - \left( {x - 1} \right) = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {{x^3} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x - 1 = 0\\
{x^3} - 1 = 0
\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}
x = 1\\
{x^3} = 1
\end{array} \right. \\\Leftrightarrow x = 1\left( \text{thỏa mãn} \right)
\end{array}\)
\(\begin{array}{l}
x + \dfrac{1}{x} = {x^2} + \dfrac{1}{{{x^2}}}\\ \Leftrightarrow \dfrac{{{x^3}}}{{{x^2}}} + \dfrac{x}{{{x^2}}} = \dfrac{{{x^4}}}{{{x^2}}} + \dfrac{1}{{{x^2}}}\\
\Rightarrow {x^3} + x = {x^4} + 1\\
\Leftrightarrow {x^4} - {x^3} - x + 1 = 0\\
\Leftrightarrow {x^3}\left( {x - 1} \right) - \left( {x - 1} \right) = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {{x^3} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x - 1 = 0\\
{x^3} - 1 = 0
\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}
x = 1\\
{x^3} = 1
\end{array} \right. \\\Leftrightarrow x = 1\left( \text{thỏa mãn} \right)
\end{array}\)
Vậy phương trình có nghiệm duy nhất x = 1.
d) ĐKXĐ: ![]() \(x \ne 0; x\ne-1\).
\(x \ne 0; x\ne-1\).
 \(\begin{array}{l}
\dfrac{{x + 3}}{{x + 1}} + \dfrac{{x - 2}}{x} = 2\\
\Leftrightarrow \dfrac{{x\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} + \dfrac{{\left( {x - 2} \right)\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{2x\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} \\\Rightarrow x\left( {x + 3} \right) + \left( {x - 2} \right)\left( {x + 1} \right) = 2x\left( {x + 1} \right)
\\\Leftrightarrow {x^2} + 3{\rm{x}} + {x^2} - 2{\rm{x}} + x - 2 = 2{{\rm{x}}^2} + 2{\rm{x}}\\
\Leftrightarrow 2{{\rm{x}}^2} + 2{\rm{x}} - 2\, - 2{{\rm{x}}^2} - 2{\rm{x}} = 0\\
\Leftrightarrow 0x = 2\left( \text{Vô nghiệm} \right)
\end{array}\)
\(\begin{array}{l}
\dfrac{{x + 3}}{{x + 1}} + \dfrac{{x - 2}}{x} = 2\\
\Leftrightarrow \dfrac{{x\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} + \dfrac{{\left( {x - 2} \right)\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{2x\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} \\\Rightarrow x\left( {x + 3} \right) + \left( {x - 2} \right)\left( {x + 1} \right) = 2x\left( {x + 1} \right)
\\\Leftrightarrow {x^2} + 3{\rm{x}} + {x^2} - 2{\rm{x}} + x - 2 = 2{{\rm{x}}^2} + 2{\rm{x}}\\
\Leftrightarrow 2{{\rm{x}}^2} + 2{\rm{x}} - 2\, - 2{{\rm{x}}^2} - 2{\rm{x}} = 0\\
\Leftrightarrow 0x = 2\left( \text{Vô nghiệm} \right)
\end{array}\)
Vậy phương trình đã cho vô nghiệm
Giải bài tập toán 8 trang 22, 23 tập 2: Luyện tập
Bài 29 (trang 22, 23 SGK Toán 8 Tập 2)
Bạn Sơn giải phương trình ![]() \(\dfrac{{{x^2} - 5x}}{{x - 5}} = 5\,\,\,\,\,\left( 1 \right)\) như sau:
\(\dfrac{{{x^2} - 5x}}{{x - 5}} = 5\,\,\,\,\,\left( 1 \right)\) như sau:
(1) ![]() \(⇔{x^2} - 5x = 5\left( {x - 5} \right)\)
\(⇔{x^2} - 5x = 5\left( {x - 5} \right)\)
![]() \(⇔{x^2} - 5x = 5x - 25\)
\(⇔{x^2} - 5x = 5x - 25\)
![]() \(⇔{x^2} - 10x + 25 = 0\)
\(⇔{x^2} - 10x + 25 = 0\)
![]() \(⇔{\left( {x - 5} \right)^2} = 0\)
\(⇔{\left( {x - 5} \right)^2} = 0\)
![]() \(⇔x = 5\)
\(⇔x = 5\)
Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức x – 5 có chứa ẩn. Hà giải bằng cách rút gọn vế trái như sau:
(1) ![]() \(⇔\dfrac{{x\left( {x - 5} \right)}}{{x - 5}} = 5 \Leftrightarrow x = 5\)
\(⇔\dfrac{{x\left( {x - 5} \right)}}{{x - 5}} = 5 \Leftrightarrow x = 5\)
Hãy cho biết ý kiến của em về hai lời giải trên.
+ Trong cách giải của bạn Sơn có ghi
(1) ⇔ ![]() \({x^2} - 5x = 5\left( {x - 5} \right)\)
\({x^2} - 5x = 5\left( {x - 5} \right)\)
Cách làm của bạn sai khi chưa đặt ĐKXĐ của phương trình đã nhân cả hai vế của phương trình với (x-5)
+ Trong cách giải của Hà có ghi
(1) ![]() \(⇔\dfrac{{x\left( {x - 5} \right)}}{{x - 5}} = 5 \Leftrightarrow x = 5\)
\(⇔\dfrac{{x\left( {x - 5} \right)}}{{x - 5}} = 5 \Leftrightarrow x = 5\)
Sai ở chỗ chưa tìm ĐKXĐ của phương trình mà lại rút gọn (x - 5).
Tóm lại cả hai cách giải đều sai ở chỗ không tìm ĐKXĐ khi giải phương trình chứa ẩn ở mẫu.
Cách giải đúng:
ĐKXĐ: ![]() \(x\ne5\)
\(x\ne5\)
 \(\eqalign{
& {{{x^2} - 5x} \over {x - 5}} = 5 \cr
& \Leftrightarrow {{{x^2} - 5x} \over {x - 5}} = {{5\left( {x - 5} \right)} \over {x - 5}} \cr
& \Rightarrow {x^2} - 5x = 5\left( {x - 5} \right) \cr
& \Leftrightarrow x\left( {x - 5} \right) - 5\left( {x - 5} \right) = 0 \cr
& \Leftrightarrow \left( {x - 5} \right)\left( {x - 5} \right) = 0 \cr
& \Leftrightarrow {\left( {x - 5} \right)^2} = 0 \cr
& \Leftrightarrow x - 5 = 0 \cr
& \Leftrightarrow x = 5\text{ (loại)} \cr}\)
\(\eqalign{
& {{{x^2} - 5x} \over {x - 5}} = 5 \cr
& \Leftrightarrow {{{x^2} - 5x} \over {x - 5}} = {{5\left( {x - 5} \right)} \over {x - 5}} \cr
& \Rightarrow {x^2} - 5x = 5\left( {x - 5} \right) \cr
& \Leftrightarrow x\left( {x - 5} \right) - 5\left( {x - 5} \right) = 0 \cr
& \Leftrightarrow \left( {x - 5} \right)\left( {x - 5} \right) = 0 \cr
& \Leftrightarrow {\left( {x - 5} \right)^2} = 0 \cr
& \Leftrightarrow x - 5 = 0 \cr
& \Leftrightarrow x = 5\text{ (loại)} \cr}\)
Vậy phương trình đã cho vô nghiệm.
Bài 30 (trang 23 SGK Toán 8 Tập 2)
Giải các phương trình:
a) ![]() \(\dfrac{1}{{x - 2}} + 3 = \dfrac{{x - 3}}{{2 - x}}\)
\(\dfrac{1}{{x - 2}} + 3 = \dfrac{{x - 3}}{{2 - x}}\)
c) ![]() \(\dfrac{{x + 1}}{{x - 1}} - \dfrac{{x - 1}}{{x + 1}} = \dfrac{4}{{{x^2} - 1}}\)
\(\dfrac{{x + 1}}{{x - 1}} - \dfrac{{x - 1}}{{x + 1}} = \dfrac{4}{{{x^2} - 1}}\)
b) ![]() \(2x - \dfrac{{2{x^2}}}{{x + 3}} = \dfrac{{4x}}{{x + 3}} + \dfrac{2}{7}\)
\(2x - \dfrac{{2{x^2}}}{{x + 3}} = \dfrac{{4x}}{{x + 3}} + \dfrac{2}{7}\)
d) ![]() \(\dfrac{{3x - 2}}{{x + 7}} = \dfrac{{6x + 1}}{{2x - 3}}\)
\(\dfrac{{3x - 2}}{{x + 7}} = \dfrac{{6x + 1}}{{2x - 3}}\)
a) ĐKXĐ: ![]() \(x \ne 2\)
\(x \ne 2\)
MTC: x - 2
Quy đồng mẫu hai vế ta được:
![]() \(\dfrac{1}{{x - 2}} + \dfrac{{3\left( {x - 2} \right)}}{{x - 2}} = - \dfrac{{x - 3}}{{x - 2}}\)
\(\dfrac{1}{{x - 2}} + \dfrac{{3\left( {x - 2} \right)}}{{x - 2}} = - \dfrac{{x - 3}}{{x - 2}}\)
Khử mẫu ta được: ![]() \(1 + 3\left( {x - 2} \right) = - \left( {x - 3} \right)\)
\(1 + 3\left( {x - 2} \right) = - \left( {x - 3} \right)\)
![]() \(\Leftrightarrow 1 + 3x - 6 = - x + 3\)
\(\Leftrightarrow 1 + 3x - 6 = - x + 3\)
![]() \(⇔ 3x + x = 3 + 6 - 1\)
\(⇔ 3x + x = 3 + 6 - 1\)
⇔ 4x = 8
⇔ x = 2 (không thỏa mãn ĐKXĐ)
Vậy phương trình vô nghiệm.
b) ĐKXĐ: ![]() \(x \ne - 3\)
\(x \ne - 3\)
MTC: 7(x + 3)
Quy đồng mẫu hai vế ta được:
![]() \(\dfrac{{2x.7.\left( {x + 3} \right)}}{{7.\left( {x + 3} \right)}} - \dfrac{{2.7.{x^2}}}{{7.\left( {x + 3} \right)}} = \dfrac{{7.4.x}}{{7.\left( {x + 3} \right)}} + \dfrac{{2\left( {x + 3} \right)}}{{7\left( {x + 3} \right)}}\)
\(\dfrac{{2x.7.\left( {x + 3} \right)}}{{7.\left( {x + 3} \right)}} - \dfrac{{2.7.{x^2}}}{{7.\left( {x + 3} \right)}} = \dfrac{{7.4.x}}{{7.\left( {x + 3} \right)}} + \dfrac{{2\left( {x + 3} \right)}}{{7\left( {x + 3} \right)}}\)
Khử mẫu ta được:
![]() \(14x\left( {x + 3} \right) - 14{x^2}= 28x + 2\left( {x + 3} \right)\)
\(14x\left( {x + 3} \right) - 14{x^2}= 28x + 2\left( {x + 3} \right)\)
![]() \(\Leftrightarrow 14{x^2} + 42x - 14{x^2}= 28x + 2x + 6\)
\(\Leftrightarrow 14{x^2} + 42x - 14{x^2}= 28x + 2x + 6\)
⇔ ![]() \(42x - 30x = 6\)
\(42x - 30x = 6\)
⇔ 12x = 6
⇔ ![]() \(x = \dfrac{6}{{12}}\)
\(x = \dfrac{6}{{12}}\)
![]() \(⇔ x= \dfrac{1}{2}\) (thỏa mãn ĐKXĐ)
\(⇔ x= \dfrac{1}{2}\) (thỏa mãn ĐKXĐ)
Vậy phương trình có nghiệm ![]() \(x =\dfrac{1}{2}\)
\(x =\dfrac{1}{2}\)
c) ĐKXĐ: ![]() \(x \ne \pm 1\)
\(x \ne \pm 1\)
MTC: ![]() \({x^2} - 1\)
\({x^2} - 1\)
Quy đồng mẫu hai vế ta được:
![]() \(\dfrac{{\left( {x + 1} \right).\left( {x + 1} \right)}}{{{x^2} - 1}} - \dfrac{{\left( {x - 1} \right).\left( {x - 1} \right)}}{{{x^2} - 1}} = \dfrac{4}{{{x^2} - 1}}\)
\(\dfrac{{\left( {x + 1} \right).\left( {x + 1} \right)}}{{{x^2} - 1}} - \dfrac{{\left( {x - 1} \right).\left( {x - 1} \right)}}{{{x^2} - 1}} = \dfrac{4}{{{x^2} - 1}}\)
Khử mẫu ta được: ![]() \({\left( {x + 1} \right)^2} - {\left( {x - 1} \right)^2} = 4\)
\({\left( {x + 1} \right)^2} - {\left( {x - 1} \right)^2} = 4\)
![]() \(\Leftrightarrow {x^2} + 2x + 1 - \left( {{x^2} - 2x + 1} \right) = 4\)
\(\Leftrightarrow {x^2} + 2x + 1 - \left( {{x^2} - 2x + 1} \right) = 4\)
![]() \(⇔{x^2} + 2x + 1 - {x^2} + 2x - 1 = 4\)
\(⇔{x^2} + 2x + 1 - {x^2} + 2x - 1 = 4\)
⇔4x = 4
![]() \(\Leftrightarrow x = 4:4\)
\(\Leftrightarrow x = 4:4\)
⇔x = 1 (không thỏa mãn ĐKXĐ)
Vậy phương trình vô nghiệm.
d) ĐKXĐ: ![]() \(x \ne - 7\) và
\(x \ne - 7\) và ![]() \(x \ne \dfrac{3}{2}\)
\(x \ne \dfrac{3}{2}\)
MTC: ![]() \((x + 7)(2x-3)\)
\((x + 7)(2x-3)\)
Quy đồng mẫu hai vế phương trình ta được:
![]() \(\dfrac{{\left( {3x - 2} \right)\left( {2x - 3} \right)}}{{\left( {x + 7} \right)\left( {2x - 3} \right)}} = \dfrac{{\left( {6x + 1} \right)\left( {x + 7} \right)}}{{\left( {x + 7} \right)\left( {2x - 3} \right)}}\)
\(\dfrac{{\left( {3x - 2} \right)\left( {2x - 3} \right)}}{{\left( {x + 7} \right)\left( {2x - 3} \right)}} = \dfrac{{\left( {6x + 1} \right)\left( {x + 7} \right)}}{{\left( {x + 7} \right)\left( {2x - 3} \right)}}\)
Khử mẫu ta được: ![]() \(\left( {3x - 2} \right)\left( {2x - 3} \right) = \left( {6x + 1} \right)\left( {x + 7} \right)\)
\(\left( {3x - 2} \right)\left( {2x - 3} \right) = \left( {6x + 1} \right)\left( {x + 7} \right)\)
![]() \(⇔6{x^2} - 9x - 4x + 6 = 6{x^2} + 42x + x + 7\)
\(⇔6{x^2} - 9x - 4x + 6 = 6{x^2} + 42x + x + 7\)
![]() \(\Leftrightarrow 6{x^2} - 13x + 6 =6 {x^2} + 43x + 7\)
\(\Leftrightarrow 6{x^2} - 13x + 6 =6 {x^2} + 43x + 7\)
![]() \(\Leftrightarrow 6{x^2} - 13x - 6{x^2} - 43x = 7 - 6\)
\(\Leftrightarrow 6{x^2} - 13x - 6{x^2} - 43x = 7 - 6\)
⇔ - 56x = 1
![]() \(⇔x =\dfrac{{ - 1}}{{56}}\) (thỏa mãn ĐKXĐ)
\(⇔x =\dfrac{{ - 1}}{{56}}\) (thỏa mãn ĐKXĐ)
Vậy phương trình có nghiệm ![]() \(x = \dfrac{{ - 1}}{{56}}\) .
\(x = \dfrac{{ - 1}}{{56}}\) .
Bài 31 (trang 23 SGK Toán 8 Tập 2)
Giải các phương trình:
a) ![]() \(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)
\(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)
b) ![]() \(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
\(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
c) ![]() \(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)
\(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)
d) ![]() \(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} = \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
\(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} = \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
a) ![]() \(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)
\(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)
Ta có: x - 1 ≠ 0⇔ x ≠ 1 và ![]() \({x^3} - 1 \ne 0\) khi
\({x^3} - 1 \ne 0\) khi ![]() \(x^3 \ne 1\) hay
\(x^3 \ne 1\) hay ![]() \(x \ne 1\)
\(x \ne 1\)
![]() \({x^2+x + 1} = {{x^2} + x + \dfrac{1}{4} + \dfrac{3}{4}}\)
\({x^2+x + 1} = {{x^2} + x + \dfrac{1}{4} + \dfrac{3}{4}}\)
 \(= {{x^2} + 2.x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\)
\(= {{x^2} + 2.x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\)
 \(= {{{\left( {x + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\)
\(= {{{\left( {x + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\)
Ta có:  \({\left( {x + \dfrac{1}{2}} \right)^2} \geqslant 0\) với mọi
\({\left( {x + \dfrac{1}{2}} \right)^2} \geqslant 0\) với mọi ![]() \(x \in\mathbb R\) nên
\(x \in\mathbb R\) nên  \({\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0\) với mọi
\({\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0\) với mọi ![]() \(x \in\mathbb R\)
\(x \in\mathbb R\)
Do đó:
ĐKXĐ: x ≠ 1
MTC: ![]() \(({x^3} - 1=(x-1)(x^2+x+1)\)
\(({x^3} - 1=(x-1)(x^2+x+1)\)
![]() \(\Leftrightarrow \dfrac{{{x^2} + x + 1}}{{{x^3} - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x\left( {x - 1} \right)}}{{{x^3} - 1}}\)
\(\Leftrightarrow \dfrac{{{x^2} + x + 1}}{{{x^3} - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x\left( {x - 1} \right)}}{{{x^3} - 1}}\)
![]() \(\Rightarrow {x^2} + x + 1 - 3{x^2} = 2x\left( {x - 1} \right)\)
\(\Rightarrow {x^2} + x + 1 - 3{x^2} = 2x\left( {x - 1} \right)\)
![]() \(\Leftrightarrow - 2{x^2} + x + 1 = 2{x^2} - 2x\)
\(\Leftrightarrow - 2{x^2} + x + 1 = 2{x^2} - 2x\)
![]() \(\Leftrightarrow 0 = 2{x^2} - 2x + 2{x^2} - x - 1\)
\(\Leftrightarrow 0 = 2{x^2} - 2x + 2{x^2} - x - 1\)
![]() \(\Leftrightarrow 0 = 4{x^2} - 3x - 1\)
\(\Leftrightarrow 0 = 4{x^2} - 3x - 1\)
![]() \(\Leftrightarrow 4{x^2} - 3x - 1 = 0\)
\(\Leftrightarrow 4{x^2} - 3x - 1 = 0\)
![]() \(\Leftrightarrow 4{x^2} - 4x+x - 1 = 0\)
\(\Leftrightarrow 4{x^2} - 4x+x - 1 = 0\)
![]() \(\Leftrightarrow 4x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\)
\(\Leftrightarrow 4x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\)
![]() \(\Leftrightarrow \left( {x - 1} \right)\left( {4x + 1} \right) = 0\)
\(\Leftrightarrow \left( {x - 1} \right)\left( {4x + 1} \right) = 0\)
![]() \(\Leftrightarrow \left[ \begin{gathered}
x - 1 = 0 \hfill \\
4x + 1 = 0 \hfill \\
\end{gathered} \right.\)
\(\Leftrightarrow \left[ \begin{gathered}
x - 1 = 0 \hfill \\
4x + 1 = 0 \hfill \\
\end{gathered} \right.\)
![]() \(\Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
4x = - 1 \hfill \\
\end{gathered} \right.\)
\(\Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
4x = - 1 \hfill \\
\end{gathered} \right.\)
 \(\Leftrightarrow \left[ {\matrix{{x = 1}\text{( loại)} \cr {x = - \dfrac{1}{4}}\text{(thỏa mãn)}\cr} }\right.\)
\(\Leftrightarrow \left[ {\matrix{{x = 1}\text{( loại)} \cr {x = - \dfrac{1}{4}}\text{(thỏa mãn)}\cr} }\right.\)
Vậy phương trình có nghiệm duy nhất ![]() \(x = - \dfrac{1}{4}\)
\(x = - \dfrac{1}{4}\)
b) ![]() \(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
\(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
ĐKXĐ: x ≠ 1, x ≠ 2, x ≠ 3
MTC: (x-1)(x-2)(x-3)
![]() \(\Rightarrow \dfrac{3(x-3)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}} + \dfrac{2(x-2)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}} = \dfrac{(x-1)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}}\)
\(\Rightarrow \dfrac{3(x-3)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}} + \dfrac{2(x-2)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}} = \dfrac{(x-1)}{{\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)}}\)
![]() \(\Rightarrow 3\left( {x - 3} \right) + 2\left( {x - 2} \right) = x - 1\)
\(\Rightarrow 3\left( {x - 3} \right) + 2\left( {x - 2} \right) = x - 1\)
![]() \(\Leftrightarrow 3x - 9 + 2x - 4 = x - 1\)
\(\Leftrightarrow 3x - 9 + 2x - 4 = x - 1\)
![]() \(\Leftrightarrow 5x - 13 = x - 1\)
\(\Leftrightarrow 5x - 13 = x - 1\)
![]() \(\Leftrightarrow 5x - x = - 1 + 13\)
\(\Leftrightarrow 5x - x = - 1 + 13\)
⇔ 4x = 12
![]() \(\Leftrightarrow x = 12:4\)
\(\Leftrightarrow x = 12:4\)
⇔ x = 3 (không thỏa mãn ĐKXĐ)
Vậy phương trình vô nghiệm.
c) ![]() \(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)
\(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)
Ta có: ![]() \(8 + {x^3} \ne 0\Leftrightarrow x^3 ≠ -8 ⇔ x ≠ -2\)
\(8 + {x^3} \ne 0\Leftrightarrow x^3 ≠ -8 ⇔ x ≠ -2\)
ĐKXĐ: x ≠ -2
MTC: ![]() \(8 + {x^3}=(x+2)(x^2-2x+4)\)
\(8 + {x^3}=(x+2)(x^2-2x+4)\)
![]() \(\Leftrightarrow \dfrac{{8 + {x^3}}}{{8 + {x^3}}} + \dfrac{{{x^2} - 2x + 4}}{{8 + {x^3}}} = \dfrac{{12}}{{8 + {x^3}}}\)
\(\Leftrightarrow \dfrac{{8 + {x^3}}}{{8 + {x^3}}} + \dfrac{{{x^2} - 2x + 4}}{{8 + {x^3}}} = \dfrac{{12}}{{8 + {x^3}}}\)
![]() \(\Rightarrow {x^3} + 8 + {x^2} - 2x + 4 = 12\)
\(\Rightarrow {x^3} + 8 + {x^2} - 2x + 4 = 12\)
![]() \(\Leftrightarrow {x^3} + {x^2} - 2x = 12 - 8 - 4\)
\(\Leftrightarrow {x^3} + {x^2} - 2x = 12 - 8 - 4\)
![]() \(\Leftrightarrow {x^3} + {x^2} - 2x = 0\)
\(\Leftrightarrow {x^3} + {x^2} - 2x = 0\)
![]() \(\Leftrightarrow x\left( {{x^2} + x - 2} \right) = 0\)
\(\Leftrightarrow x\left( {{x^2} + x - 2} \right) = 0\)
![]() \(\Leftrightarrow x\left[ {{x^2} + 2x - x - 2} \right] = 0\)
\(\Leftrightarrow x\left[ {{x^2} + 2x - x - 2} \right] = 0\)
⇔ ![]() \(x[ x(x+2) - (x+2) ] = 0\)
\(x[ x(x+2) - (x+2) ] = 0\)
⇔ ![]() \(x(x + 2)(x - 1) = 0\)
\(x(x + 2)(x - 1) = 0\)
 \(\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x + 2 = 0\\
x - 1 = 0
\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x + 2 = 0\\
x - 1 = 0
\end{array} \right.\)
 \(\Leftrightarrow \left[ \begin{array}{l}
x = 0\left( \text{ thỏa mãn} \right)\\
x = - 2\left( \text{ loại} \right)\\
x = 1\left( \text{ thỏa mãn} \right)
\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}
x = 0\left( \text{ thỏa mãn} \right)\\
x = - 2\left( \text{ loại} \right)\\
x = 1\left( \text{ thỏa mãn} \right)
\end{array} \right.\)
Vậy phương trình có tập nghiệm là ![]() \(S = \left\{ {0;1} \right\}\).
\(S = \left\{ {0;1} \right\}\).
d) ![]() \(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} = \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
\(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} = \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
ĐKXĐ: ![]() \((x \ne 3,x \ne - 3,x \ne - \dfrac{7}{2}\)
\((x \ne 3,x \ne - 3,x \ne - \dfrac{7}{2}\)
MTC: ![]() \({\left( {x - 3} \right)\left( {x + 3} \right)}\left( {2x + 7} \right)\)
\({\left( {x - 3} \right)\left( {x + 3} \right)}\left( {2x + 7} \right)\)
![]() \(\Rightarrow \dfrac{{13(x+3)}}{{(x+3)\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{(x+3)(x-3)}{{(x+3)(x-3)(2x + 7)}} = \dfrac{6(2x + 7)}{{\left( {x - 3} \right)\left( {x + 3} \right)(2x + 7)}}\)
\(\Rightarrow \dfrac{{13(x+3)}}{{(x+3)\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{(x+3)(x-3)}{{(x+3)(x-3)(2x + 7)}} = \dfrac{6(2x + 7)}{{\left( {x - 3} \right)\left( {x + 3} \right)(2x + 7)}}\)
![]() \(\Rightarrow 13\left( {x + 3} \right) + \left( {x - 3} \right)\left( {x + 3} \right) = 6\left( {2x + 7} \right)\)
\(\Rightarrow 13\left( {x + 3} \right) + \left( {x - 3} \right)\left( {x + 3} \right) = 6\left( {2x + 7} \right)\)
![]() \(\Leftrightarrow 13x + 39 + {x^2} - 9 = 12x + 42\)
\(\Leftrightarrow 13x + 39 + {x^2} - 9 = 12x + 42\)
![]() \(\Leftrightarrow {x^2} + 13x + 30 = 12x + 42\)
\(\Leftrightarrow {x^2} + 13x + 30 = 12x + 42\)
![]() \(\Leftrightarrow {x^2} + 13x + 30 - 12x - 42 = 0\)
\(\Leftrightarrow {x^2} + 13x + 30 - 12x - 42 = 0\)
![]() \(\Leftrightarrow {x^2} + x - 12 = 0\)
\(\Leftrightarrow {x^2} + x - 12 = 0\)
![]() \(\Leftrightarrow {x^2} + 4x - 3x - 12 = 0\)
\(\Leftrightarrow {x^2} + 4x - 3x - 12 = 0\)
![]() \(\Leftrightarrow x\left( {x + 4} \right) - 3\left( {x + 4} \right) = 0\)
\(\Leftrightarrow x\left( {x + 4} \right) - 3\left( {x + 4} \right) = 0\)
![]() \(\Leftrightarrow \left( {x - 3} \right)\left( {x + 4} \right) = 0\)
\(\Leftrightarrow \left( {x - 3} \right)\left( {x + 4} \right) = 0\)
![]() \(\Leftrightarrow \left[ \begin{array}{l}
x - 3 = 0\\
x + 4 = 0
\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}
x - 3 = 0\\
x + 4 = 0
\end{array} \right.\)
 \(\Leftrightarrow \left[ \begin{array}{l}
x = 3\left( \text{không thỏa mãn} \right)\\
x = - 4\left( \text{thỏa mãn} \right)
\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}
x = 3\left( \text{không thỏa mãn} \right)\\
x = - 4\left( \text{thỏa mãn} \right)
\end{array} \right.\)
Vậy phương trình có tập nghiệm là ![]() \(S = \left\{-4 \right\}\).
\(S = \left\{-4 \right\}\).
Bài 32 (trang 23 SGK Toán 8 Tập 2)
Giải các phương trình:
a) ![]() \(\dfrac{1}{x} + 2 = \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right)\)
\(\dfrac{1}{x} + 2 = \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right)\)
b)  \({\left( {x + 1 + \dfrac{1}{x}} \right)^2} = {\left( {x - 1 - \dfrac{1}{x}} \right)^2}\)
\({\left( {x + 1 + \dfrac{1}{x}} \right)^2} = {\left( {x - 1 - \dfrac{1}{x}} \right)^2}\)
a) ![]() \(\dfrac{1}{x} + 2 = \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right)\) (1)
\(\dfrac{1}{x} + 2 = \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right)\) (1)
ĐKXĐ: ![]() \(x \ne 0\)
\(x \ne 0\)
(1) ![]() \(⇔\left( {\dfrac{1}{x} + 2} \right) - \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right) = 0\)
\(⇔\left( {\dfrac{1}{x} + 2} \right) - \left( {\dfrac{1}{x} + 2} \right)\left( {{x^2} + 1} \right) = 0\)
![]() \(\Leftrightarrow\left( {\dfrac{1}{x} + 2} \right)\left( {1 - {x^2} - 1} \right)= 0\)
\(\Leftrightarrow\left( {\dfrac{1}{x} + 2} \right)\left( {1 - {x^2} - 1} \right)= 0\)
![]() \(⇔ \left( {\dfrac{1}{x} + 2} \right)\left( { - {x^2}} \right)= 0\)
\(⇔ \left( {\dfrac{1}{x} + 2} \right)\left( { - {x^2}} \right)= 0\)
 \(⇔\left[ {\matrix{{\dfrac{1}{x} + 2 = 0} \cr { - {x^2} = 0} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\dfrac{1}{x}= - 2} \cr {{x^2} = 0} \cr} } \right.\)
\(⇔\left[ {\matrix{{\dfrac{1}{x} + 2 = 0} \cr { - {x^2} = 0} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\dfrac{1}{x}= - 2} \cr {{x^2} = 0} \cr} } \right.\)
 \(\Leftrightarrow \left[ {\matrix{{x = - \dfrac{1}{2}\, (\text{thỏa mãn})} \cr {x = 0} \,(\text{loại})\cr} } \right.\)
\(\Leftrightarrow \left[ {\matrix{{x = - \dfrac{1}{2}\, (\text{thỏa mãn})} \cr {x = 0} \,(\text{loại})\cr} } \right.\)
Vậy phương trình có nghiệm duy nhất ![]() \(x = -\dfrac{{ 1}}{2}\).
\(x = -\dfrac{{ 1}}{2}\).
b)  \({\left( {x + 1 + \dfrac{1}{x}} \right)^2} = {\left( {x - 1 - \dfrac{1}{x}} \right)^2}\) (2)
\({\left( {x + 1 + \dfrac{1}{x}} \right)^2} = {\left( {x - 1 - \dfrac{1}{x}} \right)^2}\) (2)
ĐKXĐ: ![]() \(x \ne 0\)
\(x \ne 0\)
(2)  \(⇔\left[ {\matrix{{x + 1 + \dfrac{1 }{x} = x - 1 - \dfrac{1 }{x}} \cr {x + 1 + \dfrac{1}{x} = - \left( {x - 1 - \dfrac{1 }{ x}} \right)} \cr} } \right.\)
\(⇔\left[ {\matrix{{x + 1 + \dfrac{1 }{x} = x - 1 - \dfrac{1 }{x}} \cr {x + 1 + \dfrac{1}{x} = - \left( {x - 1 - \dfrac{1 }{ x}} \right)} \cr} } \right.\)
 \(\Leftrightarrow \left[ \begin{gathered}
x + 1 + \frac{1}{x} = x - 1 - \frac{1}{x} \hfill \\
x + 1 + \frac{1}{x} = - x + 1 + \frac{1}{x} \hfill \\
\end{gathered} \right.\)
\(\Leftrightarrow \left[ \begin{gathered}
x + 1 + \frac{1}{x} = x - 1 - \frac{1}{x} \hfill \\
x + 1 + \frac{1}{x} = - x + 1 + \frac{1}{x} \hfill \\
\end{gathered} \right.\)
 \(\Leftrightarrow \left[ \begin{gathered}
x + \frac{1}{x} - x + \frac{1}{x} = - 1 - 1 \hfill \\
x + \frac{1}{x} + x - \frac{1}{x} = 1 - 1 \hfill \\
\end{gathered} \right.\)
\(\Leftrightarrow \left[ \begin{gathered}
x + \frac{1}{x} - x + \frac{1}{x} = - 1 - 1 \hfill \\
x + \frac{1}{x} + x - \frac{1}{x} = 1 - 1 \hfill \\
\end{gathered} \right.\)
 \(⇔\left[ {\matrix{{\dfrac{2 }{ x} = - 2} \cr {2x = 0} \cr} \Leftrightarrow \left[ {\matrix{{x = - 1} (\text{thỏa mãn})\cr {x = 0} \text{ (loại)}\cr}} \right.} \right.\)
\(⇔\left[ {\matrix{{\dfrac{2 }{ x} = - 2} \cr {2x = 0} \cr} \Leftrightarrow \left[ {\matrix{{x = - 1} (\text{thỏa mãn})\cr {x = 0} \text{ (loại)}\cr}} \right.} \right.\)
Vậy phương trình có nghiệm duy nhất x = -1.
Bài 33 (trang 23 SGK Toán 8 Tập 2)
Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2:
a) ![]() \(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}}\)
\(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}}\)
b) ![]() \(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}}\)
\(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}}\)
a) Ta có phương trình: ![]() \(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}} = 2\);
\(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}} = 2\);
ĐKXĐ: ![]() \(a \ne - \dfrac{1}{3},a \ne - 3\)
\(a \ne - \dfrac{1}{3},a \ne - 3\)
Quy đồng hai vế phương trình ta được:
![]() \(\dfrac{{\left( {3a - 1} \right)\left( {a + 3} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}} + \dfrac{{\left( {a - 3} \right)\left( {3a + 1} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}} = \dfrac{{2\left( {3a + 1} \right)\left( {a + 3} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}}\)
\(\dfrac{{\left( {3a - 1} \right)\left( {a + 3} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}} + \dfrac{{\left( {a - 3} \right)\left( {3a + 1} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}} = \dfrac{{2\left( {3a + 1} \right)\left( {a + 3} \right)}}{{\left( {3a + 1} \right)\left( {a + 3} \right)}}\)
Khử mẫu ta được :
![]() \(\left( {3a - 1} \right)\left( {a + 3} \right) + \left( {a - 3} \right)\left( {3a + 1} \right)= 2\left( {3a + 1} \right)\left( {a + 3} \right)\)
\(\left( {3a - 1} \right)\left( {a + 3} \right) + \left( {a - 3} \right)\left( {3a + 1} \right)= 2\left( {3a + 1} \right)\left( {a + 3} \right)\)
⇔ ![]() \(3{a^2} + 9a - a - 3 + 3{a^2} - 9a + a - 3 = 6{a^2} + 18a + 2a + 6\)
\(3{a^2} + 9a - a - 3 + 3{a^2} - 9a + a - 3 = 6{a^2} + 18a + 2a + 6\)
⇔ ![]() \(6{a^2} - 6 = 6{a^2} + 20a + 6\)
\(6{a^2} - 6 = 6{a^2} + 20a + 6\)
![]() \(\Leftrightarrow 6{a^2} - 6{a^2} - 20a = 6 + 6\)
\(\Leftrightarrow 6{a^2} - 6{a^2} - 20a = 6 + 6\)
![]() \(\Leftrightarrow - 20a = 12\)
\(\Leftrightarrow - 20a = 12\)
⇔ ![]() \((a = 12:(-20)\)
\((a = 12:(-20)\)
⇔ ![]() \(a = - \dfrac{3}{5}\) (thỏa mãn)
\(a = - \dfrac{3}{5}\) (thỏa mãn)
Vậy ![]() \(a = - \dfrac{3}{5}\) thì biểu thức
\(a = - \dfrac{3}{5}\) thì biểu thức ![]() \(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}}\) có giá trị bằng 2.
\(\dfrac{{3a - 1}}{{3a + 1}} + \dfrac{{a - 3}}{{a + 3}}\) có giá trị bằng 2.
b) Ta có phương trình: ![]() \(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}} = 2\)
\(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}} = 2\)
ĐKXĐ: ![]() \(a \ne -3\)
\(a \ne -3\)
![]() \(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}} = 2\)
\(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}} = 2\)
![]() \(\Leftrightarrow \dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4(a + 3)}} - \dfrac{{7a + 2}}{{6(a + 3)}} = 2\)
\(\Leftrightarrow \dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4(a + 3)}} - \dfrac{{7a + 2}}{{6(a + 3)}} = 2\)
![]() \(\Leftrightarrow \dfrac{{4.10\left( {a + 3} \right)}}{{12\left( {a + 3} \right)}} - \dfrac{{3\left( {3a - 1} \right)}}{{12\left( {a + 3} \right)}} - \dfrac{{2\left( {7a + 2} \right)}}{{12\left( {a + 3} \right)}} = \dfrac{{2.12\left( {a + 3} \right)}}{{12\left( {a + 3} \right)}}\)
\(\Leftrightarrow \dfrac{{4.10\left( {a + 3} \right)}}{{12\left( {a + 3} \right)}} - \dfrac{{3\left( {3a - 1} \right)}}{{12\left( {a + 3} \right)}} - \dfrac{{2\left( {7a + 2} \right)}}{{12\left( {a + 3} \right)}} = \dfrac{{2.12\left( {a + 3} \right)}}{{12\left( {a + 3} \right)}}\)
Khử mẫu ta được:
![]() \(40\left( {a + 3} \right) - 3\left( {3a - 1} \right) - 2\left( {7a + 2} \right) = 24\left( {a + 3} \right)\)
\(40\left( {a + 3} \right) - 3\left( {3a - 1} \right) - 2\left( {7a + 2} \right) = 24\left( {a + 3} \right)\)
⇔ ![]() \(40a + 120 - 9a + 3 - 14a - 4 = 24a + 72\)
\(40a + 120 - 9a + 3 - 14a - 4 = 24a + 72\)
⇔ ![]() \(17a + 119 = 24a + 72\)
\(17a + 119 = 24a + 72\)
![]() \(\Leftrightarrow 17a - 24a = 72 - 119\)
\(\Leftrightarrow 17a - 24a = 72 - 119\)
⇔ ![]() \(- 7a = - 47\)
\(- 7a = - 47\)
⇔ ![]() \(a = \dfrac{{47}}{7}\) (thỏa mãn)
\(a = \dfrac{{47}}{7}\) (thỏa mãn)
Vậy ![]() \(a=\dfrac{{47}}{7}\) thì biểu thức
\(a=\dfrac{{47}}{7}\) thì biểu thức ![]() \(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}}\) có giá trị bằng 2.
\(\dfrac{{10}}{3} - \dfrac{{3a - 1}}{{4a + 12}} - \dfrac{{7a + 2}}{{6a + 18}}\) có giá trị bằng 2.
.............................
Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 5: Phương trình chứa ẩn ở mẫu. Trong quá trình học môn Toán lớp 8, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã sưu tầm và chọn lọc thêm phần Giải Toán 8 hay Giải Vở BT Toán 8 để giúp các bạn học sinh học tốt hơn.
Ngoài bài tập cơ bản môn Toán lớp 8 chuyên đề này, các bạn học sinh có thể tham khảo thêm các đề thi học kì 2 môn Toán, môn Ngữ Văn, chuẩn bị tốt kiến thức cho kì thi học kì 2 sắp tới.








