Giải Toán 8 bài 4 Đường trung bình của tam giác, của hình thang
Toán 8 bài 4: Đường trung bình của tam giác, của hình thang
Giải Toán 8 bài 4: Đường trung bình của tam giác, của hình thang được VnDoc chia sẻ dưới đây gồm lý thuyết và lời giải cho các câu hỏi và bài tập trong SGK Toán lớp 8 trang 76 - 80. Lời giải bài tập Toán 8 này sẽ giúp các em so sánh đối chiếu với kết quả bài làm, từ đó nâng cao kỹ năng giải Toán 8 và học tốt môn Toán lớp 8 hơn. Dưới đây là nội dung chi tiết, mời các em tham khảo.
I. Lý thuyết đường trung bình của tam giác, của hình thang
1. Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba,
Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
∆ABC, AD = DB, AE = EC => DE // BC, DE = ½BC
2. Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lí 1: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 2: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
II. Trả lời câu hỏi Bài 4 trang 76, 77, 78 SGK Toán 8 Tập 1
Câu hỏi 1 Trang 76 SGK Toán 8 Tập 1
Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
Hướng dẫn giải:
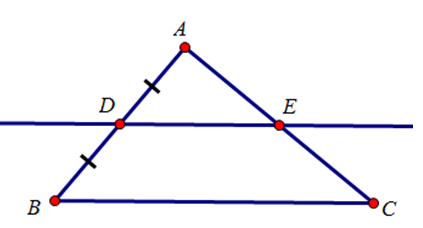
Dự đoán: E là trung điểm cạnh AC
Câu hỏi 2 Trang 77 SGK Toán 8 Tập 1
Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng rằng 
\(\widehat {ADE} = \widehat B\) và \(DE =\dfrac{1}{2}BC\)
Hướng dẫn giải:
Ta có hình vẽ như sau:
Câu hỏi 3 Trang 77 SGK Toán 8 - Tập 1
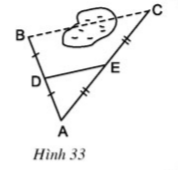
Tính độ dài đoạn BC trên hình 33.
Hướng dẫn giải:
BC = 2 DE
Câu hỏi 4 Trang 78 SGK Toán 8 - Tập 1
Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC?
Hướng dẫn giải:
Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC
Câu hỏi 5 Trang 79 SGK Toán 8 - Tập 1
Tính x trên hình 40.
Hướng dẫn giải:
Ta có:
AD ⊥ DH, CH ⊥ DH, BE ⊥ DH
=> AD // BE // CH => ADHC là hình thang
Ta lại có: B là trung điểm của AC và BE // AD // CH
=> BE là đường trung bình của hình thang ADHC
\(\begin{matrix} BE = \dfrac{{AD + CH}}{2} \hfill \\ \Rightarrow x = CH = 2.BE - AD \hfill \\ \Rightarrow x = 2.32 - 24 = 40 \hfill \\ \Rightarrow x = 40 \hfill \\ \end{matrix}\)
III. Giải bài tập Toán 8 trang 79, 80 SGK tập 1
Giải bài 20 trang 79 sgk Toán 8 tập 1
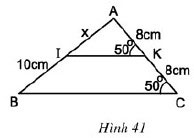
Tìm x trên hình 41.
Hướng dẫn giải
Tam giác ABC có:
\(\widehat{C} = \widehat{K} = 50^0\)
Mà \(\widehat{C}\) đồng vị với \(\widehat{K}\)
Nên BC // IK
Mặt khác KA = KC = 8, có nghĩa K là trung điểm của AC.
Theo định lí 1 về đường trung bình của tam giác thì I cũng là trung điểm của AB
Suy ra IA = IB
Mà IB = 10 nên IA = 10
Vậy x = 10cm
Bài 21 trang 79 sgk Toán 8 tập 1
Tính khoảng cách AB giữa hai mũi của compa trên hình 42 (SGK), biết rằng C là trung điểm của OA, D là trung điểm của OB và OD = 3cm.
Hướng dẫn giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = ½AB
Suy ra AB = 2CD = 2.3 = 6cm.
Bài 22 trang 80 sgk Toán 8 tập 1
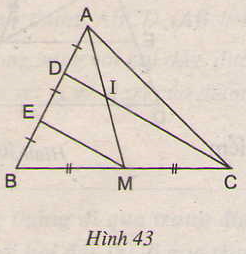
Cho hình 43. Chứng minh rằng AI = IM.
Hướng dẫn giải:
∆BDC có BE = ED và BM = MC
nên EM // DC
Suy ra DI // EM
∆AEM có AD = DE và DI // EM
nên AI = IM.
Bài 23 trang 80 sgk Toán 8 tập 1
Tìm x trên hình 44
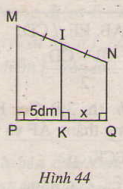
Hướng dẫn giải:
Ta có IM = IN, IK // MP // NQ nên K là trung điểm của PQ.
Do đó PK = KQ = 5
Vậy x = 5dm.
Bài 24 trang 80 sgk Toán 8 tập 1
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Hướng dẫn giải:
Hướng dẫn giải:
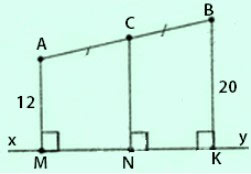
Kẻ \(AM \perp xy, CN \perp xy, BK \perp xy\) như hình vẽ.
Khi đó ta có: AM//CN//BK ⇒ ABKM là hình thang.
Suy ra CN là đường trung bình của hình thang ABKM
Do đó: \(CN = \frac{AM + BK}{2} = \frac{12 + 20}{2} = 16\)
Vậy khoảng cách từ trung điểm C của AB đến đường thẳng xy là 16cm.
Bài 25 trang 80 sgk Toán 8 tập 1
Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
Hướng dẫn giải:
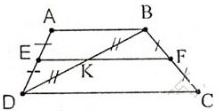
Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
IV. Giải bài tập toán 8 trang 80 tập 1: Luyện tập
Bài 26 (trang 80 SGK Toán 8 Tập 1)
Tính x, y trên hình 45, trong đó: AB//CD//EF//GH
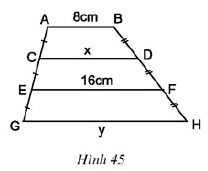
Hướng dẫn giải:
Ta có AB//EF nên ABFE là hình thang
\(\left.\begin{matrix} CA = CE\\ DB = DF\end{matrix}\right\}\)
⇒ AD là đường trung bình của hình thang ABFE
Do đó: \(CD = \frac{AB + EF}{2} = \frac{8 + 16}{2} = 12\)
Vậy x = 12cm
Tương tự ta có CD//GH nên CDHG là hình thang.
\(\left.\begin{matrix} EC = EG\\ FD = FH\end{matrix}\right\}\)
⇒ EF là đường trung bình của hình thang CDHG
Do đó: \(EF = \frac{CD + GH}{2} ⇒ GH = 2.EF – CD = 2.16 – 12 = 20\)
Vậy y = 20cm
Bài 27 (trang 80 SGK Toán 8 Tập 1)
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC
a) So sánh các độ dài EK và CD, KF và AB
b) Chứng minh rằng \(EF \leq \frac{AB + CD}{2}\)
Hướng dẫn giải:
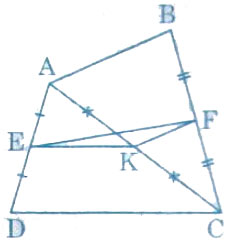
a) Ta có
\(\left.\begin{matrix} EA = ED\\ KA = KC\end{matrix}\right\}\)
⇒ EK là đường trung bình của tam giác ACD
Do đó \(EK = \frac{CD}{2}\)
Tương tự ta có:
\(\left.\begin{matrix} FB = FC\\ KA = KC\end{matrix}\right\}\)
⇒ KF là đường trung bình của tam giác ABC
Do đó \(KF = \frac{AB}{2}\)
b) Trong tam giác EFK ta có:
\(EF \leq EK + KF\)
\(⇔ EF \leq \frac{CD}{2} + \frac{AB}{2}\)
\(⇒ EF \leq \frac{AB + CD}{2} (đpcm)\)
Bài 28 (trang 80 SGK Toán 8 Tập 1)
Cho hình thang ABCD (AB//CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I, cắt AC ở K
a) Chứng minh rằng AK = KC, BI = ID
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK
Hướng dẫn giải:
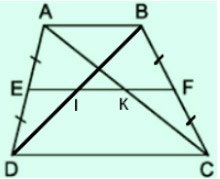
a) Ta có:
\(\left.\begin{matrix} EA = ED\\ FB = FC\end{matrix}\right\}\)
⇒ EF là đường trung bình của hình thang ABCD.
Do đó EF // AB // CD
Tam giác ABC có:
\(\left.\begin{matrix} KF // AB\\ FB = FC\end{matrix}\right\} ⇒ AK = KC\)
Tam giác ABD có:
\(\left.\begin{matrix} EA = ED\\ EI // AB\end{matrix}\right\} ⇒ BI = ID\)
b) Ta có:
EF là đường trung bình của hình thang ABCD nên:
\(EF = \frac{AB + CD}{2} = \frac{6 + 10}{2} = 8\)
EI là đường trung bình của tam giác ABD nên:
\(EI = \frac{AB}{2} = \frac{6}{2} = 3\)
KF là đường trung bình của tam giác ABC nên:
\(KF = \frac{AB}{2} = \frac{6}{2} = 3\)
Ta cũng có EF = EI + IK + KF
⇒ IK = EF – (EI + KF) = 8 – (3 + 3) = 2
Vậy EI = KF = 3cm, IK = 2cm
.......................
Bài tiếp theo: Giải Toán 8 bài 5: Dựng hình bằng thước và com-pa. Dựng hình thang
Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.
Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 4: Đường trung bình của tam giác, của hình thang. Hy vọng tài liệu sẽ giúp các em trả lời hết các câu hỏi trong phần bài tập SGK môn Toán 8 bài 4. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.
Ngoài tài liệu trên, mời các em tham khảo thêm các môn Toán 8, Văn 8, Anh 8, Hóa 8,... hoặc đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 mà chúng tôi đã sưu tầm và chọn lọc. Với Tài liệu học tập lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt.
Xem thêm:
