Dấu hiệu nhận biết hình bình hành
Dấu hiệu nhận biết hình bình hành lớp 8
Dấu hiệu nhận biết hình bình hành được VnDoc biên soạn, tổng hợp các dấu hiệu nhận biết về hình bình hành cho các bạn học sinh tham khảo, củng cố kiến thức Toán 8.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 8, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 8 sau: Tài liệu học tập lớp 8. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
I. Hình bình hành lớp 8
+ Hình bình hành là tứ giác có các cạnh đối song song.
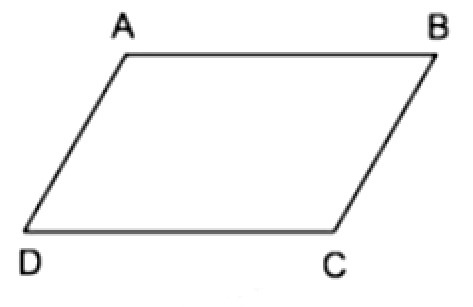
Hình bình hành ABCD có AB // CD, AD // BC
II. Tính chất hình bình hành
Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
III. Dấu hiệu nhận biết hình bình hành
1. Tứ giác có các cạnh đối song song là hình bình hành (được suy ra từ định nghĩa)
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành
Bài toán: Cho tứ giác ABCD, có AB = CD và AD = BC. Chứng minh rằng ABCD là hình bình hành.
Chứng minh:
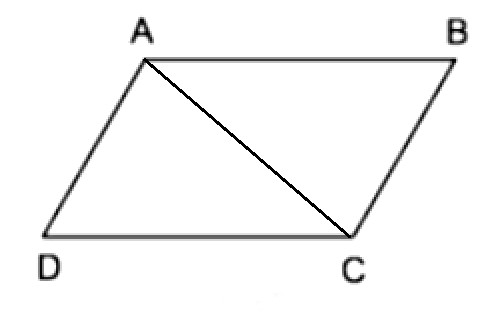
+ Nối AC.
+ Xét ∆ ADC và ∆ ABC có:
AD = BC (gt)
AB = CD (gt)
AC chung
⇒∆ADC = ∆ABC (c.c.c)
\(\Rightarrow \left\{ \begin{array}{l} \widehat {{\mathop{\rm DAC}\nolimits} } = \widehat {{\mathop{\rm BCA}\nolimits} }\\ \widehat {{\mathop{\rm ACD}\nolimits} } = \widehat {{\mathop{\rm BAC}\nolimits} } \end{array} \right.\)(cặp góc tương ứng bằng nhau)
+ Có \(\widehat {{\mathop{\rm DAC}\nolimits} } = \widehat {{\mathop{\rm BCA}\nolimits} }\)(cmt)
Mà hai góc ở vị trí so le trong
⇒AD // BC (t/c)
+ Có \(\widehat {{\mathop{\rm ACD}\nolimits} } = \widehat {{\mathop{\rm BAC}\nolimits} }\)(cmt)
Mà hai góc ở vị trí so le trong
⇒AB // CD (t/c)
+ Xét tứ giác ABCD có:
AD // BC (cmt)
AB // CD
⇒ABCD là hình bình hành (định nghĩa) (đpcm)
3. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
Bài toán: Cho tứ giác ABCD, có AB = CD và AB // CD. Chứng minh ABCD là hình bình hành.
Chứng minh:
+ Nối AC.
+ Có AB // CD \(\Rightarrow \widehat {{\mathop{\rm ACD}\nolimits} } = \widehat {{\mathop{\rm BAC}\nolimits} }\)(so le trong)
+ Xét ∆ADC và ∆ABC có:
AC chung
\(\widehat {{\mathop{\rm ACD}\nolimits} } = \widehat {{\mathop{\rm BAC}\nolimits} }\)(cmt)
AB = CD (gt)
⇒∆ADC = ∆ABC (c.g.c)
\(\Rightarrow \widehat {{\mathop{\rm DAC}\nolimits} } = \widehat {{\mathop{\rm BCA}\nolimits} }\)(cặp góc tương ứng bằng nhau)
Mà chúng ở vị trí so le trong
⇒AD // BC (t/c)
+ Xét tứ giác ABCD có:
AB // CD (gt)
AD // BC (cmt)
⇒ ABCD là hình bình hành (định nghĩa) (đpcm)
4. Tứ giác có các góc đối bằng nhau là hình bình hành
Bài toán: Cho tứ giác ABCD có \(\widehat {\mathop{\rm A}\nolimits} = \widehat {\mathop{\rm C}\nolimits} ;\widehat {\mathop{\rm B}\nolimits} = \widehat {\mathop{\rm D}\nolimits}\). Chứng minh tứ giác ABCD là hình bình hành.
Chứng minh:
+ Xét tứ giác ABCD có: \(\widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm B}\nolimits} + \widehat {\mathop{\rm C}\nolimits} + \widehat {\mathop{\rm D}\nolimits} = {180^0}\)(1) (tổng các góc trong tứ giác)
+ Có \(\widehat {\mathop{\rm A}\nolimits} = \widehat {\mathop{\rm C}\nolimits} ;\widehat {\mathop{\rm B}\nolimits} = \widehat {\mathop{\rm D}\nolimits}\)(gt) thay vào (1)
\(\Rightarrow \widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm D}\nolimits} + \widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm D}\nolimits} = {360^0} \Rightarrow \widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm D}\nolimits} = {180^0}\)
Hai góc ở vị trí trong cùng phía đối với hai đường thẳng AB và CD
⇒AB // CD
+ Có \(\widehat {\mathop{\rm A}\nolimits} = \widehat {\mathop{\rm C}\nolimits} ;\widehat {\mathop{\rm B}\nolimits} = \widehat {\mathop{\rm D}\nolimits}\)(gt) thay vào (1)
\(\Rightarrow \widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm B}\nolimits} + \widehat {\mathop{\rm A}\nolimits} + \widehat {\mathop{\rm B}\nolimits} = {360^0} \Rightarrow \widehat {\mathop{\rm A}\nolimits} + \widehat B = {180^0}\)
Hai góc ở vị trí trong cùng phía đối với hai đường thẳng AD và BC
⇒AD // BC
+ Xét tứ giác ABCD có:
AB // CD (cmt)
AD // BC (cmt)
⇒ ABCD là hình bình hành (định nghĩa) (đpcm)
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
Bài toán: Cho tứ giác ABCD, hai đường chéo AC và BD cắt nhau tại O và OB = OD, OA = OC. Chứng minh tứ giác ABCD là hình bình hành.
Chứng minh:
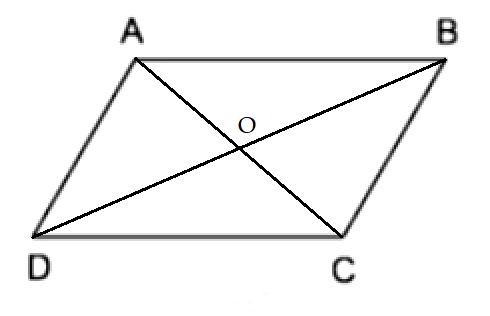
+ Xét ∆OAB và ∆OCD có:
OA = OC (gt)
\(\widehat {{\mathop{\rm AOB}\nolimits} } = \widehat {{\mathop{\rm DOC}\nolimits} }\)(đối đỉnh)
OB = OD (gt)
⇒∆OAB = ∆OCD (c.g.c)
\(\Rightarrow \widehat {{\mathop{\rm OAB}\nolimits} } = \widehat {{\mathop{\rm OCD}\nolimits} }\)(cặp góc tương ứng bằng nhau)
Mà chúng ở vị trí so le trong
⇒AB // CD (t/c)
+ Xét ∆OAD và ∆OBC có:
OA = OC (gt)
\(\widehat {{\mathop{\rm AOD}\nolimits} } = \widehat {{\mathop{\rm BOC}\nolimits} }\)(đối đỉnh)
OB = OD (gt)
⇒∆OAD = ∆OBC (c.g.c)
\(\Rightarrow \widehat {{\mathop{\rm OAD}\nolimits} } = \widehat {{\mathop{\rm OCB}\nolimits} }\)(cặp góc tương ứng bằng nhau)
Mà chúng ở vị trí so le trong
⇒AD // BC (t/c)
+ Xét tứ giác ABCD có:
AB // CD (cmt)
AD // BC (cmt)
⇒ ABCD là hình bình hành (định nghĩa) (đpcm)
IV. Bài tập về hình bình hành lớp 8
Bài 1: Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA. Chứng minh tứ giác ADME là hình bình hành.
Chứng minh:
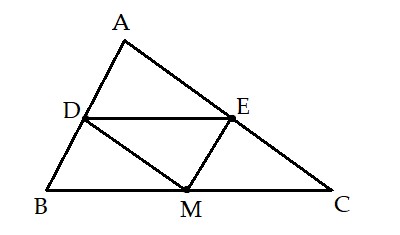
+ Xét ∆ABC có:
E là trung điểm của AC
M là trung điểm của BC
⇒EM là đường trung bình của ∆ABC (định lý) ⇒ EM // AB (t/c)
+ Xét ∆ABC có:
D là trung điểm của AB
M là trung điểm của BC
⇒MD là đường trung bình của ∆ABC (định lý) ⇒ MD // AC (t/c)
+ Xét tứ giác AEMD có:
EM // AD (EM // AB – cmt)
MD // AE (MD // AC – cmt)
⇒ AEMD là hình bình hành (dhnb) (đpcm)
Bài 2: Cho tam giác ABC, đường thẳng qua B song song với AC, cắt đường thẳng qua A song song với BC ở D. Chứng minh tứ giác ABCD là hình bình hành.
Chứng minh:
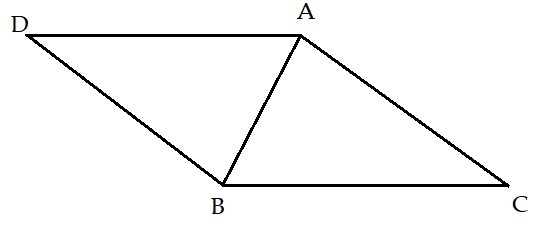
+ Xét tứ giác ABCD có:
AD // BC (gt)
BD // AC (gt)
⇒ ABCD là hình bình hành (dhnb) (đpcm)
Bài 3: Cho hình bình hành ABCD. Kẻ AE, CF vuông góc với BD. Chứng minh tứ giác AECF là hình bình hành.
Chứng minh:
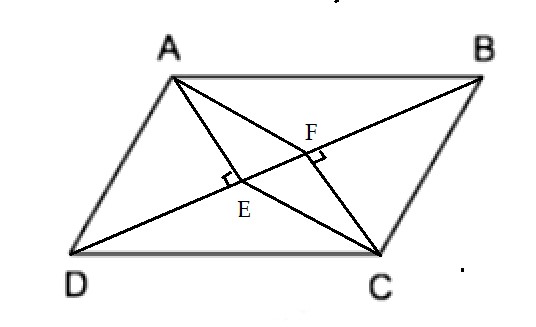
+ Có AE ⊥ BD (gt), CF ⊥BD (gt) ⇒ AE // CF (từ vuông góc đến song song)
+ Có ABCD là hình bình hành (gt)
⇒AD = BC (t/c)
+ Có ABCD là hình bình hành (gt)
⇒AD // BC (t/c) \(\Rightarrow \widehat {{\mathop{\rm ADB}\nolimits} } = \widehat {{\mathop{\rm DBC}\nolimits} }\)(so le trong)
+ Xét ∆AED và ∆CFB có:
\(\widehat {{\mathop{\rm AED}\nolimits} } = \widehat {{\mathop{\rm CFB}\nolimits} }\left( { = {{90}^0}} \right)\)
AD = BC
\(\widehat {{\mathop{\rm ADB}\nolimits} } = \widehat {{\mathop{\rm DBC}\nolimits} }\)
⇒∆AED = ∆CFB (ch – gn) ⇒ AE = CF (cạnh tương ứng)
+ Xét tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒AECF là hình bình hành (dhnb) (đpcm)
--------------
Trên đây là Các dấu hiệu nhận biết hình bình hành dành cho các bạn học sinh tham khảo để củng cố các kiến thức Toán lớp 8 chuẩn bị cho các bài thi, bài kiểm tra trong năm học. Ngoài ra mời các bạn học sinh tham khảo thêm các tài liệu như Chuyên đề Toán 8, Ngữ Văn 8, Tiếng Anh 8,..... Chúc các bạn học tốt.
