Giải bài tập SBT Toán 8 bài 6: Đối xứng trực

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 6: Đối xứng trực được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 4: Đường trung bình của tam giác, của hình thang

Giải bài tập SBT Toán 8 bài 5: Dựng hình bằng thước và comp - Dựng hình thang

Giải bài tập SBT Toán 8 bài 7: Hình bình hành

Câu 1: Cho tam giác ABC có ∠A = 70^o, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.

a, Chứng minh rằng AD = AE

b, Tính số đo góc ∠(DAE)

Lời giải:

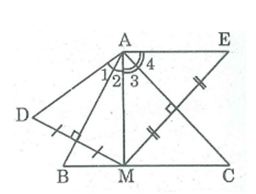
a, Vì D đối xứng với M qua trục AB

⇒ AB là đường trung trực của MD.

⇒ AD = AM (t/chất đường trung trực) (1)

Vì E đối xứng với M qua trục AC

⇒ AC là đường trung trực của ME

⇒ AM = AE (t/chất đường trung trực) (2)

Từ (1) và (2) suy ra: AD = AE

b, AD = AM suy ra ΔAMD cân tại A có AB ⊥ MD nên AB cũng là đường phân giác của ∠(MAD)

⇒ ∠A1 = ∠A2

AM = AE suy ra ΔAME cân tại A có AC ⊥ ME nên AC cũng là đường phân giác của ∠(MAE)

⇒ ∠A3 = ∠A4

∠(DAE) = ∠A1 + ∠A2 + ∠A3 + ∠A4 = 2(∠A2+ ∠A3 ) = 2∠(BAC) = 2.70^o = 140^o

Câu 2: Cho tam giác nhọn ABC có ∠A = 60^o, trực tâm H. Gọi M là điểm đối xứng với H qua BC.

a, Chứng minh ΔBHC = ΔBMC

b, Tính góc (BMC)

Lời giải:

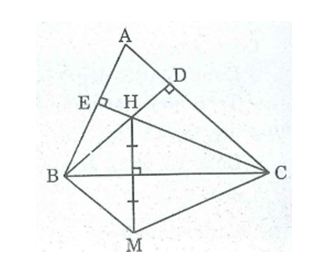
a, Vì M đối xứng với H qua trục BC

⇒ BC là đường trung trực của HM

⇒ BH = BM (t/chất đường trung trực)

CH = CM (t/chất đường trung trực)

Suy ra: ΔBHC = ΔBMC (c.c.c)

b, Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E, H là trực tâm của ΔABC

⇒ BD ⊥ AC, CE ⊥ AB

Xét tứ giác ADHE, ta có:

∠(DHE) = 360^o – (∠A + ∠D + ∠E ) = 360^o – ( 60^o + 90^o + 90^o) = 120^o

∠(BHC) = ∠(DHE)(đối đỉnh)

ΔBHC = ΔBMC (chứng minh trên)

⇒ ∠(BMC) = ∠(BHC)

Suy ra: ∠(BMC) = ∠(DHE) = 120^o

Câu 3: Cho hình thang vuông ABCD (∠A = ∠D = 90°). Gọi H là điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh rằng ∠(AIB) = ∠(DIC)

Lời giải:

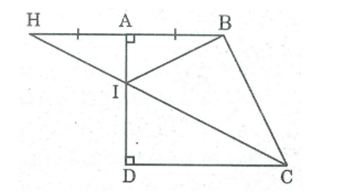
B và H đối xứng qua AD.

I và A đối xứng với chính nó qua AD

Nên ∠(AIB) đối xứng với ∠(AIH) qua AD

⇒ ∠(AIB) = ∠(AIH)

∠(AIB) = ∠(DIC) (đối đỉnh)

Suy ra: ∠(AIB) = ∠(DIC)

Câu 4: Cho hai điểm A, B thuộc cùng một nửa mặt phẳng bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kì khác C thuộc đường thẳng xy. Chứng minh rằng: AC + CB < AM + MB

Lời giải:

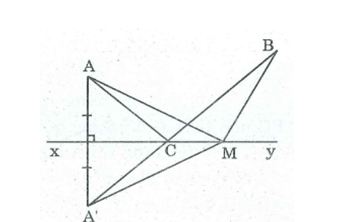
Vì A' đối xứng với A qua xy

⇒ xy là đường trung trực của AA'.

⇒ CA' = CA (t/chất đường trung trực)

MA' = MA (t/chất đường trung trực)

AC + CB = A'C + CB = A'B (1)

MA + MB = MA'+ MB (2)

Trong ΔMA'B, ta có:

A'B < A'M + MB (bất đẳng thức tam giác) (3)

Từ (1), (2) và (3) suy ra: AC + CB < AM + MB

Câu 5: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK . Chứng minh rằng điểm I đối xứng với điểm K qua AH.

Lời giải:

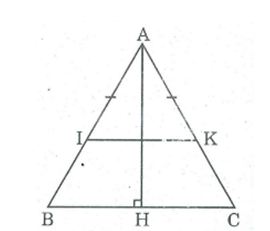
Ta có: ΔABC cân tại A; AH ⊥ BC (gt)

Suy ra: AH là tia phân giác của A

AI = AK (gt)

ΔAIK cân tại A

AH là tia phân giác của A

Nên AH là đường trung trực của IK

Vậy I đối xứng với K qua AH.

Câu 6: Tứ giác ABCD có AB = BC, AD = DC (hình cái diều). Chứng minh rằng điểm A đối xứng với điểm G qua đường thẳng BD.

Lời giải:

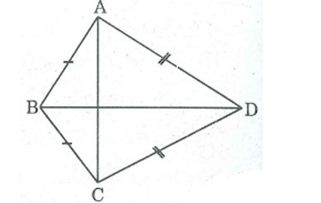
Ta có:

* BA = BC (gt)

Suy ra B thuộc đường trung trực của AC

* DC = DA (gt)

Suy ra D thuộc đường trung trực của AC

Mà B ≠ D nên BD là đường trung trực của AC

Do đó A đối xứng với C qua trục BD.

Câu 7: Cho tam giác ABC có AB < AC. Gọi d là đường thẳng trung trực của BC. Vẽ điểm K đối xứng với điểm A qua đường thẳng d

a, Tìm các đoạn thẳng đối xứng với đoạn thẳng AB qua d, đối xứng với đoạn thẳng AC qua d.

b, Tứ giác AKCB là hình gì? Vì sao?

Lời giải:

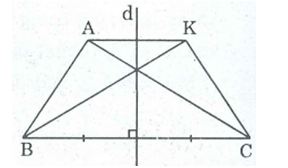
a, d là đường thẳng trung trực của BC nên B và C đối xứng qua d

K đối xứng với A qua d

Nên đoạn thẳng đối xứng với đoạn AB qua d là đoạn KC

Đoạn thẳng đối xứng với đoạn AC qua d là đoạn KB.

b, d là đường trung trực của BC (gt) ⇒ d ⊥ BC

A và K đối xứng qua d nên d lả trung trực của AK ⇒ d ⊥ AK

Suy ra: BC //AK. Tứ giác ABCK là hình thang.

AC và KB đối xứng qua d nên AC = BK

Vậy hình thang ABCK là hình thang cân.

Câu 8: Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC+ CB < AM+ MB

Lời giải:

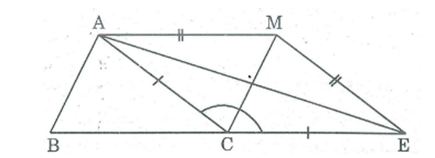
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ΔACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)

⇒ MA = ME (tỉnh chất đường trung trực)

Ta có: AB + BC = BC + ME (1)

MA + MB = MB + ME (2)

Trong ΔMBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)

Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.

Câu 9: Trong các hình nét đậm vẽ trên giấy kẻ ô vuông Ở hình 4, hình 5, hình nào có trục đối xứng.

Lời giải:

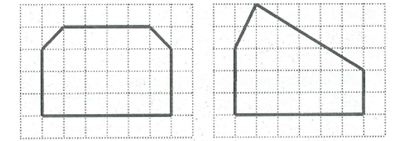
Hình 4 là hình có trục đối xứng.

Câu 10: Chứng minh rằng giao điểm hai đường chéo hình thang cân nằm trên trục đối xứng của hình thang cân.

Lời giải:

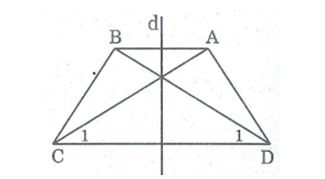
Hình thang cân ABCD có AB // CD

Gọi O là giao điểm của hai đường chéo AC và BD.

Xét ΔADC và ΔBCD:

AD = BC (tính chất hình thang cân)

AC = BD (tính chất hình thang cân)

CD chung

Do đó ΔADC= ΔBCD (c.c.c)

⇒ ∠D1= ∠C1

⇒ΔOCD cân tại O

⇒ OC = OD nên O nằm trên đường trung trực của CD.

Trục đối xứng hình thang cân là đường thẳng trung trực của hai đáy.

Vậy O thuộc trục đối xứng của hình thang cân.