Giải bài tập SBT Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài: Ôn tập chương 2

Giải bài tập SBT Toán 8 bài 1: Mở đầu về phương trình

Giải bài tập SBT Toán 8 bài 3: Phương trình đưa về dạng ax + b = 0

Câu 1: Bằng quy tắc chuyển vế, giải các phương trình sau:

a, x – 2,25 = 0,75

b, 19,3 = 12 – x

c, 4,2 = x + 2,1

d, 3,7 – x = 4

Lời giải:

a, x – 2,25 = 0,75 ⇔ x = 0,75 + 2,25 ⇔ x = 3

b, 19,3 = 12 – x ⇔ x = 12 – 19,3 ⇔ x = - 7,3

c, 4,2 = x + 2,1 ⇔ x = 4,2 – 2,1 ⇔ x = 2,1

d, 3,7 – x = 4 ⇔ 3,7 – 4 = x ⇔ x = - 0,3

Câu 2: Bằng quy tắc nhân, tìm giá trị gần đúng nghiệm của các phương trình sau (làm tròn đến chữ số thập phân thứ ba).

a, 2x = √13

b, –5x = 1 + √5

c, x√2 = 4√3

Lời giải:

a, 2x = √13 ⇔ x = √13/2 ⇔ x ≈ 1,803

b, – 5x = 1 + √5 ⇔ x = (- 1 + √5) / 5 ⇔ x≈ -0,647

c, x√2 = 4√3 ⇔ x = 4√3 / √2 ⇔ x ≈ 4,899

Câu 3: Tìm giá trị của m sao cho phương trình sau đây nhận x = -2 là nghiệm: 2x + m = x – 1

Lời giải:

Thay x = -2 vào hai vế của phương trình, ta có:

2.(-2) + m = - 2 – 1 ⇔ -4 + m = -3 ⇔ m = 1

Vậy với m = 1 thì phương trình 2x + m = x – 1 nhận x = -2 là nghiệm.

Câu 4: Tìm giá trị của k, biết rắng một trong hai phương trình sau đây nhận x = 5 là nghiệm, phương trình còn lại nhận x = -1 là nghiệm: 2x = 10 và 3 – kx = 2

Lời giải:

Thay x = 5 vào vế trái của phương trình 2x = 10, ta thấy giá trị của hai vế bằng nhau. Vậy x = 5 là nghiệm của phương trình 2x = 10.

Khi đó x = -1 là nghiệm của phương trình 3 – kx = 2.

Thay x = -1 vào phương trình 3 – kx = 2, ta có:

3 – k(-1) = 2 ⇔ 3 + k = 2 ⇔ k = -1

Vậy k = -1.

Câu 5: Giải các phương trình sau:

a, 7x + 21 = 0

b, 5x – 2 = 0

c, 12 – 6x = 0

d, -2x + 14 = 0

Lời giải:

a, 7x + 21 = 0 ⇔ 7x = -21 ⇔ x = -3

b, 5x – 2 = 0 ⇔ 5x = 2 ⇔ x = 2/5

c, 12 – 6x = 0 ⇔ 12 = 6x ⇔ x = 2

d, -2x + 14 = 0 ⇔ -2x = -14 ⇔ x = 7

Câu 6: Giải các phương trình sau:

a, 0,25x + 1,5 = 0

b, 6,36 – 5,3x = 0

c, 4/3 x - 5/6 = 1/2

d, -5/9 x + 1 = 2/3 x – 10

Lời giải:

a, 0,25x + 1,5 = 0 ⇔ 0,25x = -1,5 ⇔ x = -6

b, 6,36 – 5,3x = 0 ⇔ 6,36 = 5,3x ⇔ x = 1,2

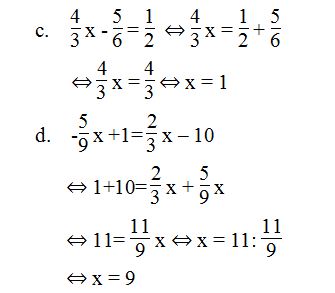
Câu 7: Giải các phương trình sau:

a, 3x + 1 = 7x – 11

b, 5 – 3x = 6x + 7

c, 11 – 2x = x – 1

d, 15 – 8x = 9 – 5x

Lời giải:

a, 3x + 1 = 7x – 11 ⇔ 3x – 7x = -11 – 1 ⇔ -4x = -12 ⇔ x = 3

b, 5 – 3x = 6x + 7 ⇔ 5 – 7 = 6x + 3x ⇔ -2 = 9x ⇔ x = -29

c, 11 – 2x = x – 1 ⇔ 11 + 1 = x + 2x ⇔ 12 = 3x ⇔ x = 4

d, 15 – 8x = 9 – 5x ⇔ -8x + 5x = 9 – 15 ⇔ -3x = -6 ⇔ x = 2

Câu 8: Chứng tỏ rằng các phương trình sau đây vô nghiệm:

a, 2(x + 1) = 3 + 2x

b, 2(1 – 1,5x) + 3x = 0

c, |x| = -1

Lời giải:

a, Ta có: 2(x + 1) = 3 + 2x ⇔ 2x + 2 = 3 + 2x ⇔ 0x = 1

Vậy phương trình vô nghiệm.

b, Ta có: 2(1 – 1,5x) + 3x = 0 ⇔ 2 – 3x + 3x = 0 ⇔ 2 + 0x = 0

Vậy phương trình vô nghiệm.

c, Vì |x| ≥ 0 nên phương trình |x| = -1 vô nghiệm.

Câu 9: Cho phương trình (m² – 4)x + 2 = m. Giải phương trình trong mỗi trường hợp sau:

a, m = 2

b, m = -2

c, m = -2,2

Lời giải:

a, Khi m = 2, phương trình đã cho trở thành:

(2² – 4)x + 2 ⇔ 0x + 2 = 2 ⇔ 2 = 2

Vậy phương trình đã cho có vô số nghiệm.

b, Khi m = -2, phương trình đac cho trở thành:

[(-2)² – 4]x + 2 = -2 ⇔ 0x + 2 = -2 ⇔ 0x = -4

Vậy phương trình đã cho vô nghiệm.

c, Khi m = -2,2, phương trình đã cho trở thành:

[(-2,2)² – 4]x + 2 = -2,2 ⇔ 0,84x + 2 = -2,2

⇔ 0,84x = -2,2 – 2 ⇔ 0,84x = -4,2 ⇔ x = -5

Vậy phương trình đã cho có nghiệm x = -5.