Bài tập Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8
Toán lớp 8: Hình chóp tứ giác đều, hình chóp tam giác đều
Hình chóp đều tam giác, hình chóp đều tứ giác lớp 8 được VnDoc biên soạn, giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
1. Hình chóp tam giác đều

a. Hình chóp tam giác đều có:
- Đáy là tam giác đều
- Mặt bên là các tam giác cân bằng nhau có chung đỉnh
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của tam giác đáy.
- Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy là đường cao của hình chóp.
- Đường cao vẽ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tam giác đều.
b. Diện tích của hình chóp tam giác đều
– Diện tích xung quanh của hình chóp bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p . d
(với p là nửa chu vi đáy, d là trung đoạn)
– Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích mặt đáy:
Stp = Sxq + Sđáy
c. Thể tích hình chóp tam giác đều:
– Thể tích của hình chóp bằng ![]() tích của diện tích đáy với chiều cao của nó:
tích của diện tích đáy với chiều cao của nó:
![]()
Trong đó: S là diện tích đáy;
h là chiều cao của hình chóp
Ví dụ 1: Cho hình chóp tam giác đều có chiều dài cạnh đáy là 3 dm và trung đoạn của hình chóp tam giác đều là 15 cm. Tính diện tích xung quanh của hình chóp đó.
Lời giải:
Nửa chu vi đáy của hình chóp là:
p = (3 x 3) : 2 = 4,5 dm = 45 cm
Diện tích xung quanh của hình chóp là:
Sxq = 45 . 15 = 675 (cm2)
2. Hình chóp tứ giác đều

a. Hình chóp tứ giác đều có:
- Mặt đáy là hình vuông
- Các mặt bên là các tam giác cân bằng nhau có chung đỉnh
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm các đều các đỉnh của mặt đáy (giao điểm của hai đường chéo)
b. Diện tích hình chóp tứ giác đều
• Diện tích xung quanh của hình chóp đều sẽ bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p . d
(với p là nửa chu vi đáy, d là trung đoạn)
• Diện tích toàn phần của hình chóp sẽ bằng tổng của diện tích xung quanh và diện tích mặt đáy. Ta có công thức sau đây:
Stp = Sxq + Sđáy
c. Thể tích hình chóp tứ giác đều
– Thể tích của hình chóp bằng ![]() tích của diện tích đáy với chiều cao của nó:
tích của diện tích đáy với chiều cao của nó:
![]()
Trong đó: S là diện tích đáy;
h là chiều cao của hình chóp
Ví dụ 2: Cho khối chóp tứ giác SABCD có tất cả các cạnh có độ dài bằng a. Chứng minh rằng SABCD là chóp tứ giác đều. Tính thể tích khối chóp SABCD.
Lời giải: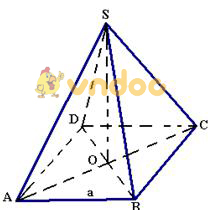
Dựng SO ⊥ (ABCD)
Ta có SA = SB = SC = SD nên OA = OB = OC = OD
⇒ ABCD là hình thoi có đường tròn ngoại tiếp nên ABCD là hình vuông.
Ta có SA2 + SB2 = AB2 + BC2 = AC2 nên Δ ASC vuông tại S
![]()
![]()
3. Phân biệt hình chóp tam giác đều và hình chóp tứ giác đều:
– Hình chóp tam giác đều theo định nghĩa là hình chóp đều có đáy là tam giác (mặt bên là tam giác cân, chưa đều).
– Hình chóp tứ giác đều theo định nghĩa là hình chóp đều có đáy là tứ giác (lúc này đáy là hình vuông, mặt bên là tam giác cân).
4. Bài tập hình chóp tam giác đều và hình chóp tứ giác đều
Câu 1: Thể tích của hình chóp tứ giác đều có chiều cao là 9 cm, cạnh đáy là 5 cm là:
| A. 75 cm3 | B. 225 cm3 | C. 180 cm3 | D. 60 cm3 |
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3 cm, chiều cao của hình chóp là h = 2 cm. Thể tích của hình chóp đã cho là:
| A. 6 cm3 | B. 18 cm3 | C. 12 cm3 | D. 9 cm3 |
Câu 3: Cho hình chóp tam giác đều có độ dài cạnh đáy là 5 cm, độ dài trung đoạn của hình chóp là 6 cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
| A. 40 cm2 | B. 36 cm2 | C. 45 cm2 | D. 50 cm2 |
Câu 4. Diện tích xung quanh của hình chóp đều bằng
A. Tích nửa chu vi đáy và chiều cao của hình chóp
B. Tích nửa chu vi đáy và trung đoạn
C. Tích chu vi đáy và trung đoạn
D. Tổng chu vi đáy và trung đoạn
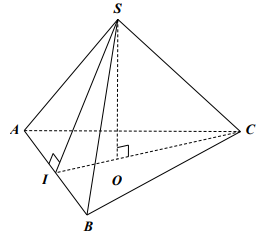
Câu 5: Cho hình chóp tam giác đều S.ABC, có cạnh đáy AB = 7 cm và độ dài trung đoạn SI = 8 cm (hình vẽ bên). Tính diện tích xung quanh của hình chóp S.ABC
Câu 6: Một chiếc lều có hình dạng là một hình chóp tứ giác đều. Biết chiếc lều có mặt bên là tam giác đều có cạnh bằng 2 m. Tính chiều cao của chiếc lều.

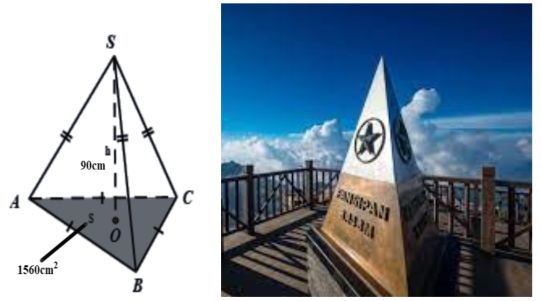
Câu 7: Chóp inox đặt trên đỉnh núi Fansipan (Việt Nam) có dạng hình chóp tam giác đều với diện tích đáy khoảng 1 560 cm2 và chiều cao khoảng 90 cm. Tính thể tích của chóp inox trên đỉnh núi Fansipan (Việt Nam).
Câu 8: Một khối bê tông có dạng như hình vẽ bên.

Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 40 cm và chiều cao là 25 cm. Phần trên của khối bê tông là hình chóp tứ giác đều có cạnh đáy bằng 40 cm và chiều cao bằng 100 cm. Tính thể tích khối bê tông?
Câu 9: Một hình chóp tứ giác đều có cạnh đáy 5 cm, trung đoạn 6,5 cm, chiều cao hình chóp là 6 cm. Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều ?
Câu 10: Cho hình chóp tứ giác đều có chu vi mặt đáy bằng 40 cm, trung đoạn bằng 13 cm, chiều cao hình chóp bằng 12 cm. Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều?
Câu 11: Một hình chóp tứ giác đều có chiều cao bằng 15 cm, trung đoạn bằng 17 cm, độ dài cạnh đáy của hình chóp bằng 16 cm. Tính diện tích xung quanh, diện tích toàn phần (tổng diện tích các mặt của hình chóp), thể tích của hình chóp tứ giác đều?
Bài 12: Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh đáy là 72 dm, chiều cao là 68,1 dm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là 77 dm.
---------------------------









