Giải bài tập SBT Toán 8 bài 8: Các trường hợp đồng dạng của tam giác vuông
Bài tập môn Toán lớp 8
Giải bài tập SBT Toán 8 bài 8: Các trường hợp đồng dạng của tam giác vuông được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Giải bài tập SBT Toán 8 bài 6: Trường hợp đồng dạng thứ hai (c.g.c)
Giải bài tập SBT Toán 8 bài 7: Trường hợp đồng dạng thứ ba (g.g)
Giải bài tập SBT Toán 8 bài: Ôn tập chương III
Câu 1: Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD.
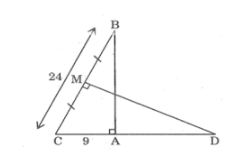
Lời giải:
Xét hai tam giác vuông ABC và MDC, ta có:
∠(BAC) = ∠(DMC ) = 90°
∠C chung
Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)
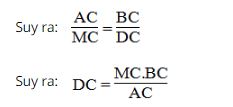
Ta có: MC = 1/2 .BC = 1/2 .24 = 12 (cm)
Vây DC = (12.24)/9 = 32 (cm)
Câu 2: Cho hình thang vuông ABCD (∠A = ∠D = 90o) AD = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh ∠(BEC) = 90o
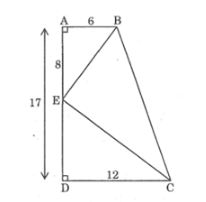
Lời giải:
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét ΔABE và ΔDEC, ta có:
∠A = ∠D = 90o (1)

Từ (1) và (2) suy ra: ΔABE đồng dạng ΔDEC (c.g.c)
Suy ra: ∠(AEB) = ∠(DEC)
Trong ΔABE ta có: ∠A = 90o ⇒ ∠(ABE) + ∠(AEB) = 90o
Suy ra: ∠(DEC) + ∠(AEB) = 90o
Lại có: ∠(ABE) + ∠(BEC) +∠(DEC) =∠(AED) = 180o (kề bù)
Vậy: ∠(BEC) = 180o- (∠(DEC) + ∠(AEB) ) = 180o - 90o = 90o
Câu 3: Cho tam giác ABC vuông tại A, AC =4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD =9cm. Chứng minh rằng BD // AC
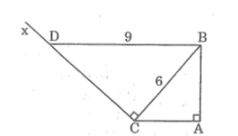
Lời giải:
Xét hai tam giác vuông ABC và CDB, ta có:
∠(BAC) = ∠(DCB) = 90o (1)
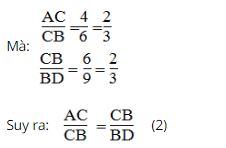
Từ (1) và (2) suy ra: ΔABC đồng dạng ΔCDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: ∠(ACB) = ∠(CBD)
Câu 4: Trên hình vẽ hãy chỉ ra các tam giác đồng dạng .Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng
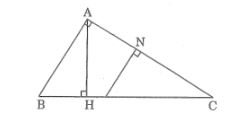
Lời giải:
-ΔABC đồng dạng ΔHBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
-ΔABC đồng dạng ΔHAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
-ΔABC đồng dạng ΔNMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
-ΔHAC đồng dạng ΔNMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
-ΔHAC đồng dạng ΔHBA
Hai tam giác vuông có góc nhọn ∠(HBA) = ∠(HAC)
-ΔHAB đồng dạng ΔNCM
Hai tam giác vuông có góc nhọn ∠(HAB) = ∠(NCM)
Câu 5: Cho tam giác ABC (∠A = 90o) có đường cao AH. Chứng minh rằng AH2 = BH.CH
Lời giải:
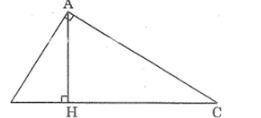
Xét hai tam giác vuông HBA và HAC, ta có:
∠(HBA) = ∠(AHC) = 90o
∠B = ∠(HAC) (hai góc cùng phụ C)
Suy ra: ΔHBA đồng dạng ΔHAC (g.g)
Suy ra: HA/HB = HC/HA
Vậy AH2 = BH.CH
Câu 6: Tam giác vuông ABC (A = 90o) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm
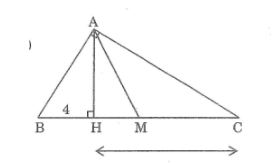
Lời giải:
Xét hai tam giác vuông HBA,HAC có:
∠(BHA) = ∠(AHC) = 90o
∠B = ∠(HAC) (hai góc cùng phụ ∠C)
⇒ΔHBA đồng dạng ΔHAC (g.g)
Suy ra: HA/HB = HC/HA
⇒ HA2 = HB.HC = 4.9 = 36(cm)
Suy ra: AH = 6(cm)
Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6.5cm
Mà HM = BM – BH = 6,5 – 4 = 2,5cm
Vậy SAHM = 1/2 AH.HN = 1/2 .6.2,5 = 7,5cm2








