Giải bài tập SBT Toán 8 bài 12: Chia đa thức một biến đã sắp xếp

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 12: Chia đa thức một biến đã sắp xếp được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 10: Chia đơn thức cho đơn thức

Giải bài tập SBT Toán 8 bài 11: Chia đa thức cho đơn thức

Giải bài tập SBT Toán 8 bài: Ôn tập chương 1

Câu 1: Làm tính chia:

a, (6x² + 13x – 5) : (2x + 5)

b, (x³ – 3x² + x – 3) : (x – 3)

c, (2x⁴ + x³ – 5x² – 3x – 3) : (x² – 3)

Lời giải

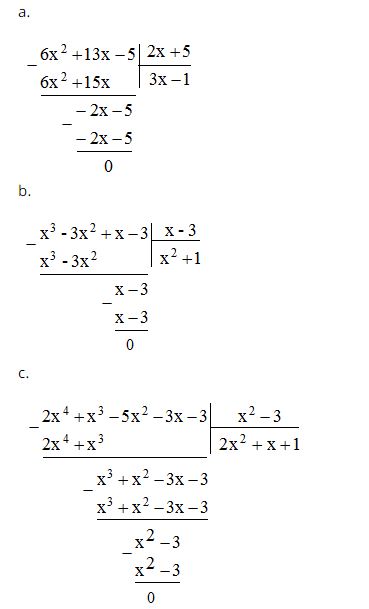
Câu 2: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:

a, (12x² – 14x + 3 – 6x³ + x⁴) : (1 – 4x + x²)

b, (x⁵ – x² – 3x⁴ + 3x + 5x³ – 5) : (x² – 3x + 5)

c, (2x² – 5x³ + 2x + 2x⁴ – 1) : (x² – x – 1)

Lời giải:

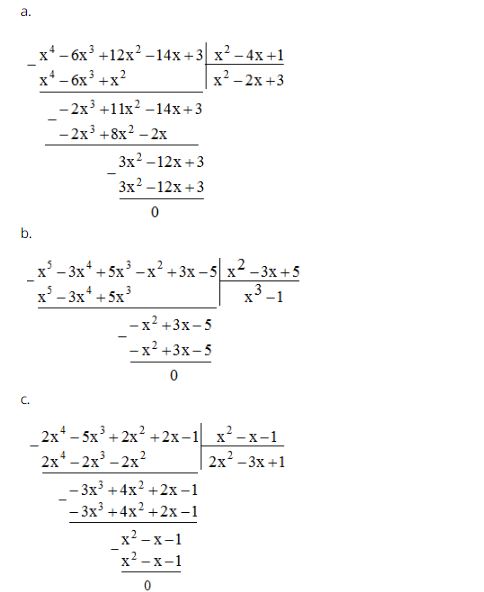
Câu 3: Cho hai đa thức A = x⁴ – 2x³ + x² + 13x -11 và B = x² – 2x + 3. Tìm thương Q và số dư R sao cho A = b,Q + R.

Lời giải:

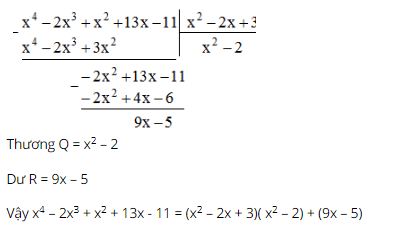
Câu 4: Tìm a để đa thức x⁴ – x³ + 6x² - x + a chia hết cho đa thức x² – x + 5

Lời giải:

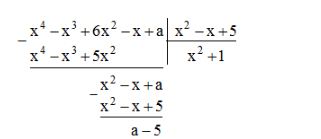
Để có phép chia hết thì số dư phải bằng 0.

Ta có: a – 5 = 0 hay a = 5.

Câu 5: Tìm giá trị nguyên của n để giá trị biểu thức 3n³ + 10n² – 5 chia hết cho giá trị của biểu thức 3n + 1.

Lời giải:

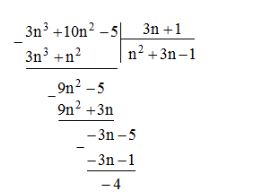
Ta có: 3n³ + 10n² – 5 = (3n + 1)(n² + 3n – 1) – 4

Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)

3n + 1 ∈ {-4; -2; -1; 1; 2; 4}

3n + 1 = -4⇒ 3n = -5⇒ n = ∉ Z : loại