Giải bài tập SBT Toán 8 bài 1: Mở đầu về phương trình

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 1: Mở đầu về phương trình được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 9: Biến đổi các biểu thức hữu tỉ - Giá trị của phân thức

Giải bài tập SBT Toán 8 bài: Ôn tập chương 2

Giải bài tập SBT Toán 8 bài 2: Phương trình bậc nhất một ẩn và cách giải

Câu 1: Hãy thử lại và cho biết các khẳng định sau có đúng không:

a, x³ + 3x = 2x² – 3x + 1 ⇔ x = -1;

b, (z – 2)(z2 + 1) = 2z + 5 ⇔ z = 3

Lời giải:

a, x³ + 3x = 2x2 – 3x + 1 ⇔ x = -1. Kết luận này sai vì thay x = -1 vào hai vế:

- Vế trái: (-1)³ + 3(-1) = -1 + (-3) = -4

- Vế phải: 2(-1)² – 3(-1) + 1 = 2.1 + 3 + 1 = 6

b, (z – 2)(z² + 1) = 2z + 5 ⇔ z = 3. Kết luận này sai vì thay z = 3 vào hai vế:

- Vế trái: (3 – 2)(3² + 1) = 1.10 = 10

- Vế phải: 2.3 + 5 = 11

Câu 2: Cho ba biểu thức 5x – 3; x² – 3x + 12 và (x + 1)(x – 3)

a, Lập ba phương trình, mỗi phương trình có hai vế là hai trong ba biểu thức đã cho.

b, Hãy tính giá trị của các biểu thức đã cho khi x nhận tất cả các giá trị thuộc tập hợp M = {x ∈Z |-5 ≤ x ≤ 5}, điền vào bảng sau rồi cho biết mỗi phương trình ở câu a có những nghiệm nào trong tập hợp M.

Lời giải:

a, 5x – 3 = x² – 3x + 12 (1)

5x – 3 = (x + 1)(x – 3) (2)

x² – 3x + 12 = (x + 1)(x – 3) (3)

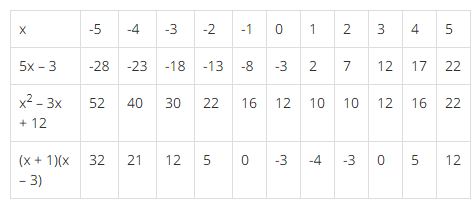
b, {x ∈Z |-5 ≤ x ≤ 5} ⇒ x ∈ {-5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5}

Phương trình (1) có nghiệm là x = 3 và x = 5.

Phương trình (2) có nghiệm là x = 0.

Phương trình (3) không có nghiệm.

Câu 3: Trong một cửa hàng bán thực phẩm, Tâm thấy cô bán hàng dùng một chiếc cân đĩa. Một bên cô đặt một quả cân 500g, bên đĩa kia, cô đặt hai gói hàng như nhau và ba quả cân nhỏ, mỗi quả 50g thì cân thăng bằng. Nếu mỗi gói hàng là x (gam) thì điều đó có thể được mô tả bởi phương trình nào?

Lời giải:

Nếu gói hàng là x (g) thì việc làm của cô bán hàng thể hiện bởi phương trình 2x + 150 = 500

Câu 4: Thử lại rằng phương trình 2mx - 5 = - x + 6m - 2 luôn luôn nhận x = 3 là nghiệm, dù m lấy bât cứ giá trị nào.

Lời giải:

Thay x = 3 vào từng vế của phương trình, ta có:

- Vế phải: -3 + 6m – 2 = 6m – 5

- Vế trái: 2m.3 – 5 = 6m – 5

Điều đó chứng tỏ rằng x = 3 luôn là nghiệm của phương trình với bất kỳ giá trị nào của m.

Câu 5: Cho hai phương trình x² - 5x + 6 = 0 (1) và x + (x - 2)(2x + 1) = 2 (2)

a, Chứng minh rằng hai phương trình có chung nghiệm là x = 2.

b, Chứng tỏ x = 3 là nghiệm của (1) nhưng không là nghiệm của (2).

c, Hai phương trình đã cho có tương đương với nhau không, vì sao?

Lời giải:

a, Thay x = 2 vào vế trái phương trình (1):

2² – 5.2 + 6 = 4 – 10 + 6 = 0

Vế trái bằng vế phải, vậy x = 2 là nghiệm của phương trình (1).

Thay x = 2 vào vế trái phương trình (2):

2 + (2 - 2) (2.2 + l) = 2 + 0 = 2

Vế trái bằng vế phải, vậy x = 2 là nghiệm của phương trình (2).

b, Thay x = 3 vào vế trái phương trình (1):

3² - 5.3 + 6 = 9 – 15 + 6 = 0

Vế trái bằng vế phải, vậy x = 3 là nghiệm của phương trình (1).

Thay x = 3 vào vế trái phương trình (2):

3 + (3 - 2) (2.3 + l) = 3 + 7 = 10

Vế trái khác vế phải, vậy x = 3 không phải là nghiệm của phương trình (2).

c, Hai phương trình đó không tương đương vì x = 3 là nghiệm của phương trình (1) mà không phải là nghiệm của phương trình (2).

Câu 6: Tại sao có thể kết luận tập nghiệm của phương trình √x + 1 = 2√-x là ∅?

Lời giải:

Tập nghiệm của phương trình √x + 1 = 2√-x là ∅ vì:

Nếu x = 0 thì hai vế có giá trị khác nhau

Nếu x < 0 thì √x không xác định vì số âm không có căn bậc hai.

Nếu x > 0 thì √-x không xác định vì số âm không có căn bậc hai.

Câu 7: Chứng minh rằng phương trình x + |x| = 0 nghiệm đúng với mọi x ≤ 0

Lời giải:

x ≤ 0 ⇒ |x| = -x

Suy ra: x + |x| = x – x = 0

Vậy mọi x ≤ 0 đều là nghiệm của phương trình x + |x| = 0

Câu 8: Cho phương trình (m² + 5m + 4) x² = m + 4, trong đó m là một số. Chứng minh rằng:

a, Khi m = - 4, phương trình nghiệm đúng với mọi giá trị của ẩn

b, Khi m = - l, phương trình nghiệm vô nghiệm.

c, Khi m = - 2 hoặc m = -3, phương trình vô nghiệm.

d, Khi m = 0 phương trình nhận x = l và x = - l là nghiệm.

Ta có phương trình (m² + 5m + 4) x2 = m + 4

Lời giải:

a, Thay m = - 4 vào vế trái phương trình:

[(-4)² + 5(-4) + 4] x² = 0x²

Vế phải phương trình : - 4 + 4 = 0

Phương trình đã cho trở thành:

0x2 = 0 nghiệm đúng với mọi giả trị của x ∈ R.

b, Thay m = - l vào vế trái phương trình : [(- l)² + 5 (- l) + 4] x2 = 0x²

Vế phải phương trình : - l + 4 = 3

Phương trình đã cho trở thành : 0x² = 3 không có giá trị nào của x thỏa mãn phương trình. Vậy phương trình vô nghiệm.

c, Thay m = - 2 vào vế trái phương trình : [( 2)² + 5(- 2) + 4] x² = - 2x²

Vế phải phương trình: - 2 + 4 = 2

Phương trình đã cho trở thành: - 2x² = 2 không có giả trị nào của x thỏa mãn vì vế trái âm mà vế phải dương. Vậy phương trình vô nghiệm.

Thay m = - 3 vào về trái phương trình: [(- 3)2 + 5 (- 3) + 4] x² = - 2x²

Vế phải phương trình : - 3 + 4 = l

Phương trình đã cho trở thành: - 2x² = l không có giả trị nào của x thỏa mãn vì vế trái là số âm mà vế phải là số dương. Vậy phương trình vô nghiệm.

d, Khi m = 0 phương trình trở thành 4x² = 4 nhận x = 1 và x = -1 là nghiệm. Vì thay x = 1 và x = -1 thì hai vế phương trình có giá trị bằng nhau.

Trên đây VnDoc đã giới thiệu tới các bạn Giải bài tập SBT Toán 8 bài 1: Mở đầu về phương trình. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc