Giải Toán 8 bài 1: Đa giác. Đa giác đều
Giải bài tập Toán 8 bài 1: Đa giác. Đa giác đều
Giải SGK Toán 8 bài 1: Đa giác. Đa giác đều với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.
Trả lời câu hỏi Toán 8 Tập 1 Bài 1 trang 114
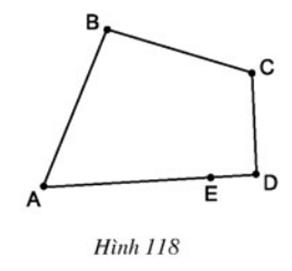
Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác?
Lời giải
Hình 118 không phải là một đa giác vì DE và EA cùng nằm trên một đường thẳng
Trả lời câu hỏi Toán 8 Tập 1 Bài 1 trang 114:
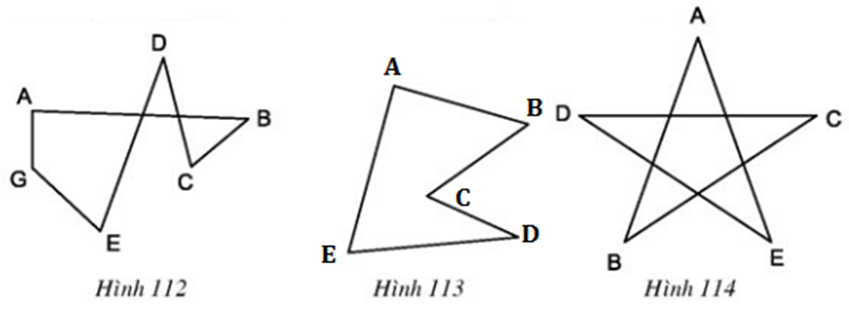
Tại sao các đa giác ở hình 112, 113, 114 không phải là đa giác lồi?
Lời giải
- Hình 112: Đa giác nằm trên hai nửa mặt phẳng có bờ AB (hoặc bờ DE, hoặc bờ DC)
- Hình 113: Đa giác nằm trên hai nửa mặt phẳng có bờ BC (hoặc bờ CD)
- Hình 114: Đa giác nằm trên hai nửa mặt phẳng có bờ AB/ BC/ CD/ DE/ EA
Trả lời câu hỏi Toán 8 Tập 1 Bài 1 trang 114:
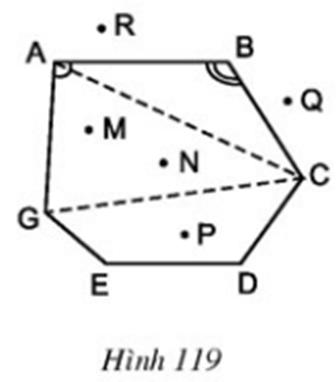
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:
Các đỉnh là các điểm: A, B, …
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …
Các cạnh là các đoạn thẳng: AB, BC, …
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …
Các góc là: ∠A , ∠B , …
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …
Lời giải
Các đỉnh là các điểm: A, B, C, D, E, G
Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc C và D, hoặc D và E, hoặc E và G, hoặc G và A
Các cạnh là các đoạn thẳng: AB, BC, CD, DE, EG, GA
Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, AD, AE, BG, BE, BD, CE, DG
Các góc là: ∠A, ∠B, ∠C, ∠D, ∠E, ∠G
Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, P
Các điểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, R
Trả lời câu hỏi Toán 8 Tập 1 Bài 1 trang 115:
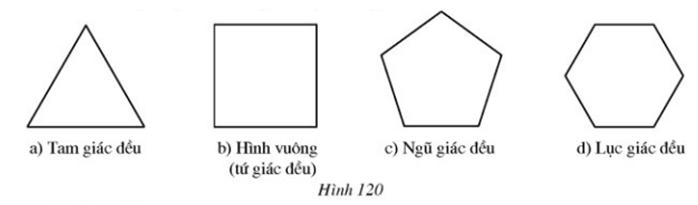
Hãy vẽ các trục đối xứng và tâm đối xứng của mỗi hình 120a, b, c, d (nếu có)
Lời giải
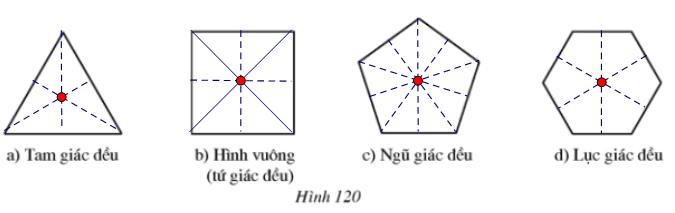
a) Trục đối xứng là các đường trung trực của tam giác đều
Tâm đối xứng là giao điểm ba đường trung trực
b) Trục đối xứng là đường thẳng nối hai trung điểm của hai cạnh đối nhau của hình vuông và hai đường chéo
Tâm đối xứng là giao điểm hai đường chéo
c) Trục đối xứng là đường thẳng nối đỉnh và trung điểm cạnh đối diện đỉnh đó
Tâm đối xứng là giao điểm của các trục đối xứng
d) Trục đối xứng là đường thẳng nối hai trung điểm của hai cạnh đối nhau của lục giác đều
Tâm đối xứng là giao điểm của các trục đối xứng
Bài 1 (trang 115 SGK Toán 8 Tập 1):
Hãy vẽ phác một lục giác lồi.
Hãy nêu cách nhận biết một đa giác lồi.
Lời giải:
- Lục giác lồi ABCDEF
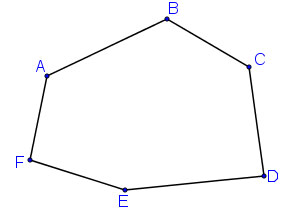
- Cách nhận biết một đa giác lồi: Một đa giác lồi là một đa giác thỏa mãn điều kiện sau:
+ Các cạnh chỉ cắt nhau tại các đỉnh, nghĩa là không có hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đa giác thỏa mãn điều kiện này là đa giác đơn.
+ Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa giác đơn thỏa mãn thêm điều kiện này là một đa giác lồi.
Bài 2 (trang 115 SGK Toán 8 Tập 1): Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:
a) Có tất cả các cạnh bằng nhau.
b) Có tất cả các góc bằng nhau.
Lời giải:
a) Hình thoi có tất cả các cạnh bằng nhau nhưng các góc có thể không bằng nhau nên hình thoi không buộc phải là đa giác đều.
b) Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh có thể không bằng nhau nên hình chữ nhật không buộc phải là đa giác đều.
Bài 3 (trang 115 SGK Toán 8 Tập 1):
Cho hình thoi ABCD có góc ∠A = 60o. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
Lời giải:
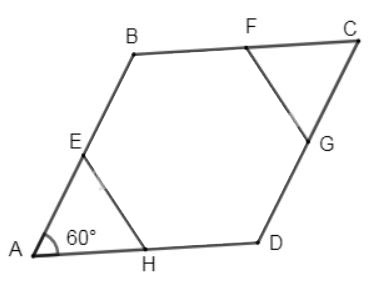
Vì ABCD là hình thoi (giả thiết) và 
\(\widehat A = {60^0}\) (giả thiết)
Do đó \(AB = BC = CD = DA; AB//DC;\,BC//AD.\)
Lại có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA nên \(AE = EB = BF = FC = CG = GD\, = DH = HA\)
Vì AD//BC nên \(\widehat A + \widehat {ABC} = {180^0}\) (2 góc trong cùng phía bù nhau)
\(\Rightarrow \widehat {ABC} = {180^0} - \widehat A = {180^0} - {60^0} = {120^0}\)
\(\Rightarrow \widehat {ABC} = \widehat {ADC} = {120^0}\) (tính chất hình thoi)
\(\Delta EAH\) có AE = AH (chứng minh trên) và \(\widehat A=60^0\) nên là tam giác đều (vì tam giác cân có một góc 60^0 là tam giác đều)
\(\Rightarrow \widehat {AEH} = \widehat {AHE} = {60^0}\)và AE = EH = AH (tính chất tam giác đều)
\(\left\{ \begin{array}{l} \widehat {AEH} + \widehat {HEB} = {180^0}\\ \widehat {AHE} + \widehat {EHD} = {180^0} \end{array} \right. (hai góc kề bù)\)
\(\Rightarrow \widehat {HEB} = \widehat {EH{\rm{D}}} = {180^0} - {60^0} = {120^0}\)
Tương tự:
\(\Delta CFG\) có CF=CG (chứng minh trên) và \(\widehat C=\widehat A =60^0\) (do ABCD là hình thoi) nên là \Delta CFG tam giác đều (vì tam giác cân có một góc \(60^0\) là tam giác đều)
\(\Rightarrow \widehat {CFG} = \widehat {CGF} = {60^0}\) và CF = FG = CG (tính chất tam giác đều)
\(\left\{ \begin{array}{l} \widehat {CFG} + \widehat {BFG} = {180^0}\\ \widehat {CGF} + \widehat {FGD} = {180^0} \end{array} \right. (hai góc kề bù)\)
\(\Rightarrow \widehat {BFG} = \widehat {FGD} = {180^0} - {60^0} = {120^0}\)
Từ đó ta suy ra: \(EB = BF = GD=HD\, = EH= FG\)
\(\widehat {ABC} = \widehat {ADC} =\widehat {HEB} = \widehat {EH{\rm{D}}}=\widehat {BFG} =\widehat{F GD} = {120^0}\)
Vậy đa giác EBFGDH có tất cả các góc bằng nhau, tất cả các cạnh bằng nhau (bằng nửa cạnh hình thoi)
Nên EBFGDH là một lục giác đều (dấu hiệu nhận biết lục giác đều)
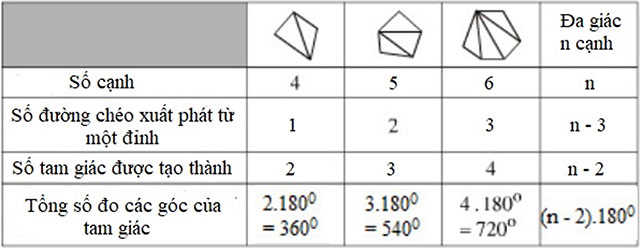
Điền số thích hợp vào các ô trống trong bảng sau:
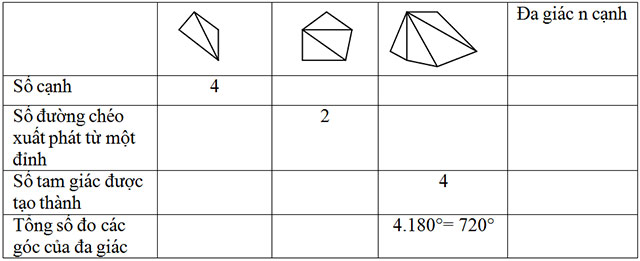
Lời giải:
Bài 5 (trang 115 SGK Toán 8 Tập 1)
Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n – giác đều.
Lời giải:
Tổng số đo các góc của hình n- giác bằng \((n - 2).180^{\circ}\)
Suy ra số đo mỗi góc của hình n- giác đều là \(\dfrac{\left ( n-2 \right ).180^{\circ}}{n}\)
Áp dụng công thức trên, ta có:
- Số đo mỗi góc của ngũ giác đều là \(\dfrac{\left ( 5-2 \right ).180^{\circ}}{5}=108^0\)
- Số đo mỗi góc của lục giác đều là \(\dfrac{\left ( 6-2 \right ).180^{\circ}}{6} = 120^{\circ}\)
............................
Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải Toán 8 bài 1: Đa giác. Đa giác đều. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.
Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải SBT Toán 8, Giải Vở BT Toán 8 và các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa... được cập nhật liên tục trên VnDoc.
