Công thức tính diện tích hình thoi, chu vi hình thoi

Hình thoi là gì? Công thức tính diện tích hình thoi, chu vi hình thoi như thế nào? Mời các bạn tham khảo tài liệu dưới đây bao gồm các công thức diện tích, chu vi diện tích hình thoi để các bạn nắm vững các kiến thức, tính chất, dấu hiệu cách tính diện tích hình thoi và áp dụng tính toán trong các bài tập môn Toán lớp 8. Mời các em cùng tham khảo bài viết.

• Công thức tính diện tích hình tam giác, chu vi hình tam giác
• Công thức tính chu vi hình chữ nhật và diện tích hình chữ nhật
• Công thức tính diện tích hình vuông, chu vi hình vuông
• Công thức tính chu vi hình bình hành, diện tích hình bình hành

A. Hình Thoi là gì?

1. Định nghĩa

Hình thoi là hình tứ giác có 4 cạnh bằng nhau và có một số tính chất như: 2 góc đối bằng nhau, 2 đường chéo vuông góc với nhau và cắt tại trung điểm của mỗi đường đồng thời là đường phân giác của các góc. Hình thoi có đầy đủ các tính chất của hình bình hành.

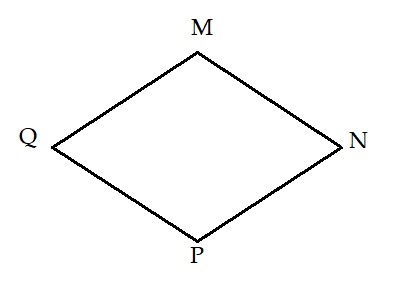
Hình thoi MNPQ có MN = NP = PQ = QM và QM//PN, MN//PQ

2. Tính chất

Hình thoi có tất cả các tính chất của hình bình hành. Ngoài ra, trong hình thoi:

+ Hai đường chéo vuông góc với nhau.

+ Hai đường chéo là các đường phân giác của các góc của hình thoi.

3. Dấu hiệu nhận biết

+ Tứ giác có bốn cạnh bằng nhau là hình thoi.

+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

B. Công thức tính diện tích hình thoi

Diện tích hình thoi bằng 1 nửa tích của 2 đường chéo:

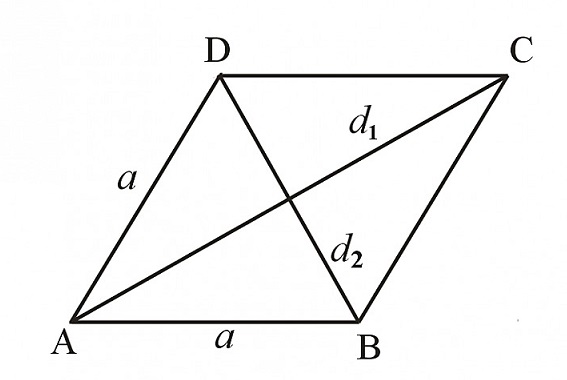
Hình thoi ABCD với 2 đường chéo d_1, d₂

Công thức tính diện tích hình thoi

\({{\mathop{\rm S}\nolimits} _{ABCD}} = \frac{1}{2}{d_1}{d_2}\)

với d₁, d₂ lần lượt là 2 đường chéo của hình thoi.

* Tính diện tích hình thoi khi biết cạnh kề và góc

Ví dụ: Cho hình thoi ABCD có AD = 5m, \(\widehat {\mathop{\rm A}\nolimits} = {30^0}\). Tính diện tích của hình thoi.

Lời giải:

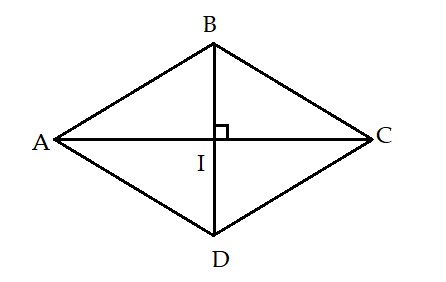
+ Gọi I là giao điểm của AC và BD.

+ Xét tam giác ABD có AB = AD và AI ⊥ BD

⟶ AI là đường phân giác của \(\widehat {{\mathop{\rm BAD}\nolimits} }\)

⟶\(\widehat {{\mathop{\rm BA}\nolimits} {\mathop{\rm I}\nolimits} } = \widehat {{\mathop{\rm DAI}\nolimits} } = {15^0}\)

⟶AI = AB.cosIAB = 5.cos15⁰ = 4,8 (m)

+ Xét tam giác vuông ABI có: BI² = AB² – AI² (định lý Pitago)

⟶ BI = 1,4(m)

+ Có BD = 2.BI = 2.1,4 = 2,8 (m)

+ \({S_{{\mathop{\rm ABCD}\nolimits} }} = 2.{S_{{\mathop{\rm ABD}\nolimits} }} = 2.\frac{1}{2}.{\mathop{\rm BD}\nolimits} .AI = 2.\frac{1}{2}.2,8.4,8 = 13,44\)(m²)

* Tính diện tích của hình thoi biết độ dài cạnh và độ dài 1 đường chéo

Ví dụ: Cho hình thoi ABCD có AB = 10m, AC = 16m. Tính diện tích của hình thoi,

Lời giải:

+ Gọi I là giao điểm của AC và BD.

⟶IC = AC : 2 = 8 (m)

+ Xét tam giác vuông BEC có: BI² = BC² – IC² (định lý Pitago)

⟶BI = 6 (m)

+ Có BD = 2.BI = 2.6 = 12(m)

+\({S_{{\mathop{\rm ABCD}\nolimits} }} = \frac{1}{2}.{\mathop{\rm BD}\nolimits} .A{\mathop{\rm C}\nolimits} = \frac{1}{2}.12.16 = 96\) (m²)

C. Công thức tính chu vi của hình thoi

Công thức, cách tính diện tích hình thoi, chu vi hình thoi

\({{\mathop{\rm P}\nolimits} _{ABCD}} = 4a\)

Với a là chiều dài của cạnh hình thoi

Vì Hình thoi có đầy đủ tính chất của hình bình hành nên học sinh có thể áp dụng tính diện tích hình bình hành hoặc hình thang để tính diện tích hình thoi.

D. Bài tập vận dụng

1. Bài tập hình thoi

Bài 1: Tính chu vi của hình thoi ABCD có độ dài AB = 5cm.

Bài 2: Hai đường chéo của hình thoi có độ dài 6cm và 8cm. Tính chu vi hình thoi đó.

Bài 3: Cho hình thoi ABCD có chu vi bằng 20cm, đường chéo BD = 6cm. Tính độ dài đường chéo AC.

Bài 4: Tính diện tích của hình thoi ABCD, biết: BD = 9m, AC = 15m

Bài 5: Một hình thoi có diện tích 4dm², độ dài một đường chéo là 5dm. Tính độ dài đường chéo thứ hai.

Bài 6: Một khi đất hình thoi có độ dài các đường chéo là 70m và 300m. Tính diện tích của khu đất đó.

Bài 7: Khoanh vào chữ đặt trước hình có diện tích lớn nhất:

A. Hình vuông có cạnh là 5cm.

B. Hình chữ nhật có chiều dài 6cm và chiều rộng 4cm.

C. Hình bình hành có diện tích 20cm²

D. Hình thoi có độ dài các đường chéo là 10cm và 6cm.

2. Đáp án bài tập hình thoi

Bài 1:

Chu vi của hình thoi ABCD là: 5.4 = 20 (cm)

Bài 2:

+ Gọi I là giao điểm của AC và BD. Khi đó IB = BD : 2 = 3(cm) và IA = AC : 2 = 4(cm)

+ Xét tam giác vuông IAB có: IA² + IB² = AB² (định lý Pitago)

⟶AB = 5 (cm)

+ Chu vi của hình thoi ABCD là: 5.4 = 20(cm)

Bài 3:

+ Gọi I là giao điểm của AC và BD. Khi đó IB = BD : 2 = 3(cm)

+ Độ dài AB = 20 : 4 = 5 (cm)

+ Xét tam giác vuông IAB có IA² + IB² = AB² (định lý Pitago)

⟶IA = 4 (cm)

+ Có AC = 2.IA = 2.4 = 8(cm)

Bài 4:

\({S_{{\mathop{\rm ABCD}\nolimits} }} = \frac{1}{2}.{\mathop{\rm BD}\nolimits} .A{\mathop{\rm C}\nolimits} = \frac{1}{2}.9.15 = 67,5\)(cm²)

Bài 5:

Độ dài đường chéo thứ hai là: 2.4 : 5 = 1,6(dm)

Bài 6:

Diện tích của khu đất đó là: 70.300 : 2 = 10500(m²)

Bài 7: Đáp án đúng là đáp án D.

A. Diện tích hình vuông là 5.5 = 25cm²

B. Diện tích hình chữ nhật là 4.6 = 24cm²

C. Hình bình hành có diện tích 20cm²

D. Diện tích hình thoi là 6.10:2 = 30cm²

---------

Ngoài Công thức tính diện tích hình thoi, chu vi hình thoi,  mời các bạn tham khảo thêm Giải Toán 8, Giải Bài tập Toán 8, Chuyên đề Toán 8, đề thi học kì 1 lớp 8, đề thi học kì 2 lớp 8 để học tốt môn Toán hơn và chuẩn bị cho các bài thi đạt kết quả cao.

Mời các bạn học sinh tham khảo thêm tài liệu liên quan:

• Diện tích hình chữ nhật
• Diện tích tam giác
• Diện tích hình thang
• Diện tích hình thoi