VnDoc.com

Giải Toán 8 bài 7: Trường hợp đồng dạng thứ ba

Giải SGK Toán 8 bài 7

Bài trước

Tải về

Bài sau

Giải bài tập Toán 8 bài 7: Trường hợp đồng dạng thứ ba

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 78:
Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 79:
Bài 35 (trang 79 SGK Toán 8 tập 2):
Bài 36 (trang 79 SGK Toán 8 Tập 2)
Bài 37 (trang 79 SGK Toán 8 tập 2):
Bài 38 (trang 79 SGK Toán 8 tập 2):
Bài 39 (trang 79, 80 SGK Toán 8 Tập 2)
Bài 40 (trang 80 SGK Toán 8 tập 2):
Bài 41 (trang 80 SGK Toán 8 tập 2):
Bài 42 (trang 80 SGK Toán 8 tập 2):
Bài 43 (trang 80 SGK Toán 8 tập 2):
Bài 44 (trang 80 SGK Toán 8 tập 2):
Bài 45 (trang 80 SGK Toán 8 tập 2):

Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 78:

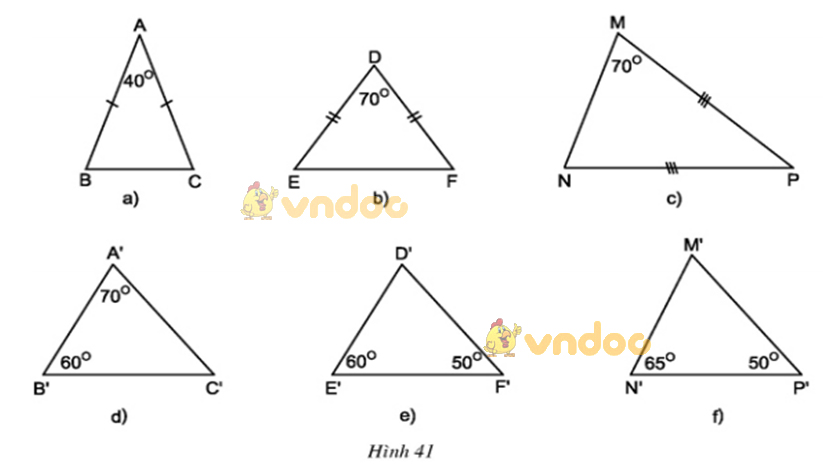
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau? Hãy giải thích (h.41)

Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Lời giải

- ΔABC có ∠A + ∠B + ∠C = 180^o

Mà ΔABC cân tại A ⇒ ∠B = ∠C

⇒∠B + ∠C = 180^o - ∠A ⇒ ∠B = ∠C = (180^o - 40^o)/2 = 70^o

ΔMNP cân tại P ⇒ ∠M = ∠N = 70^o

ΔABC và ΔPMN có

∠B = ∠M = 70^o)

∠C = ∠N = 70^o)

⇒ ΔABC ∼ ΔPMN (g.g)

- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180^o

⇒∠C' = 180^o - (∠A' + ∠B') = 180^o - (70^o + 60^o) = 50^o

ΔA’B’C’ và ΔD’E’F’ có

(∠B' = ∠E' = 60^o)

∠C' = ∠F' = 50^o)

⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 79:

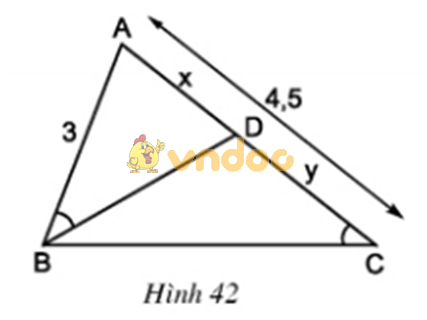
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).

a) Trong hình vẽ này có bao nhiêu tam giác? Có cặp tam giác nào đồng dạng với nhau không?

b) Hãy tính các độ dài x và y (AD = x, DC = y).

c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.

Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Lời giải

a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC

ΔABD và ΔACB có

∠B = ∠C

∠A chung

⇒ ΔABD ∼ ΔACB (g.g)

b) ΔABD ∼ ΔACB

$\Rightarrow \frac{AB}{AD}=\frac{AC}{AB}\Rightarrow \frac{3}{AD}=\frac{4,5}{3}$ $\Rightarrow \frac{AB}{AD}=\frac{AC}{AB}\Rightarrow \frac{3}{AD}=\frac{4,5}{3}$

$\Rightarrow \ AD\ =\ x\ =\ \frac{3\times3}{4,5}=2$ $\Rightarrow \ AD\ =\ x\ =\ \frac{3\times3}{4,5}=2$

⇒ y = 4,5 – 2 = 2,5

c) BD là tia phân giác của góc B

$\Rightarrow \frac{AB}{BC}=\frac{x}{y}\Rightarrow \frac{3}{BC}=\frac{2}{2,5}$ $\Rightarrow \frac{AB}{BC}=\frac{x}{y}\Rightarrow \frac{3}{BC}=\frac{2}{2,5}$

$\Rightarrow \ BC\ =\ \frac{3\times2,5}{2}=3,375$ $\Rightarrow \ BC\ =\ \frac{3\times2,5}{2}=3,375$

Ta có: ΔABD ∼ ΔACB

$\Rightarrow \frac{AB}{BD}=\frac{AC}{BC}\Rightarrow \frac{3}{BD}=\frac{4,5}{3,75}$ $\Rightarrow \frac{AB}{BD}=\frac{AC}{BC}\Rightarrow \frac{3}{BD}=\frac{4,5}{3,75}$

$\Rightarrow \ BD=\frac{3\times3,75}{4,5}=2,5$ $\Rightarrow \ BD=\frac{3\times3,75}{4,5}=2,5$

Bài 35 (trang 79 SGK Toán 8 tập 2):

Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k.

Lời giải:

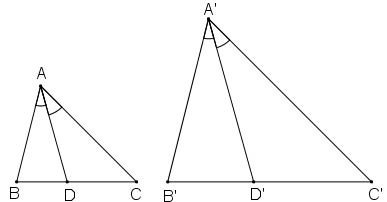
Gọi AD, A'D' lần lượt là đường phân giác của hai tam giác ABC; A'B'C'

Ta có: ∆A'B'C' ∽ ∆ABC theo tỉ số $k= \dfrac{A$ $k= \dfrac{A'B'}{AB}$

$\Rightarrow \widehat {BAC} = \widehat {B$ $\Rightarrow \widehat {BAC} = \widehat {B'A'C'}$ (1) (tính chất hai tam giác đồng dạng)

AD là phân giác góc $\widehat {BAC}$ $\widehat {BAC}$ (gt)

$\Rightarrow\widehat {BAD} = \dfrac{1}{2}\widehat {BAC}$ $\Rightarrow\widehat {BAD} = \dfrac{1}{2}\widehat {BAC}$ (2) (tính chất tia phân giác)

A'D' là phân giác góc $\widehat {B$ $\widehat {B'A'C'}$ (gt)

$\Rightarrow\widehat {B$ $\Rightarrow\widehat {B'A'D'} =\dfrac{1}{2}\widehat {B'A'C'}$ (3) (tính chất tia phân giác)

Từ (1),(2) và (3) suy ra: $\widehat{BAD} = \widehat{B$ $\widehat{BAD} = \widehat{B'A'D'}$

Xét ∆A'B'D' và ∆ABD có:

+) $\widehat{B} = \widehat{B$ $\widehat{B} = \widehat{B'}$ (vì ∆A'B'C' ∽ ∆ABC)

+) $\widehat{BAD} = \widehat{B$ $\widehat{BAD} = \widehat{B'A'D'}$ (chứng minh trên)

$\Rightarrow ∆A$ $\Rightarrow ∆A'B'D' ∽ ∆ABD$ (g-g)

$\Rightarrow \dfrac{A$ $\Rightarrow \dfrac{A'D'}{AD}=\dfrac{A'B'}{AB}=k$

Bài 36 (trang 79 SGK Toán 8 Tập 2)

Tính độ dài x của đoạn thẳng BD trong hình 43 (làm tròn đến chữ số thập phân thứ nhất), biết rằng ABCD là hình thang (AB // CD); AB = 12,5cm, CD = 28,5cm;

$\widehat{DAB} = \widehat{DBC}$ $\widehat{DAB} = \widehat{DBC}$

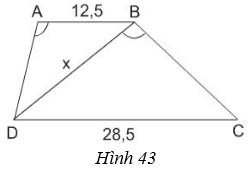
Lời giải:

Xét ∆ABD và ∆BDC có:

+) $\widehat{DAB} = \widehat{DBC}$ $\widehat{DAB} = \widehat{DBC}$ (giả thiết)

+) $\widehat{ABD} = \widehat{BDC}$ $\widehat{ABD} = \widehat{BDC}$ (AB//CD, hai góc so le trong)

$\Rightarrow ∆ABD ∽ ∆BDC$ $\Rightarrow ∆ABD ∽ ∆BDC$ (g-g)

$\Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}$ $\Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow B{D^2} = AB.DC$ $\Rightarrow B{D^2} = AB.DC$

$\Rightarrow BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \approx 18,9 cm$ $\Rightarrow BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \approx 18,9 cm$

Bài 37 (trang 79 SGK Toán 8 tập 2):

Hình 44 cho biết góc EBA = góc BDC.

a) Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích của hai tam giác AEB và BCD.

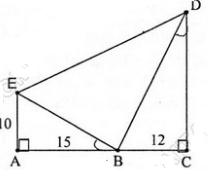
Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Hình 44

Lời giải:

a) Ta có: $\widehat{EBA} = \widehat{BDC}$ $\widehat{EBA} = \widehat{BDC}$ (giả thiết) mà $\widehat{BDC} + \widehat{CBD}={90^0}$ $\widehat{BDC} + \widehat{CBD}={90^0}$ (do tam giác BCD vuông tại C)

$\Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}$ $\Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}$

Vậy $\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD}) = {180^o} - {90^o} = {90^o}$ $\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD}) = {180^o} - {90^o} = {90^o}$

Vậy trong hình vẽ có ba tam giác vuông đó là:

∆ABE, ∆CBD, ∆EBD.

b) ∆ABE và ∆CDB có:

$\widehat{A} = \widehat{C}=90^o$ $\widehat{A} = \widehat{C}=90^o$

$\widehat{ABE}= \widehat{CDB}$ $\widehat{ABE}= \widehat{CDB}$ (giả thiết)

$\Rightarrow ∆ABE ∽ ∆CDB$ $\Rightarrow ∆ABE ∽ ∆CDB$ (g-g)

$\Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}$ $\Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)$ $\Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)$

- Áp dụng định lí pitago ta có:

∆ABE vuông tại A

$\Rightarrow BE = \sqrt{AE^{2}+AB^{2}}=\sqrt{10^{2}+15^{2}} \approx 18\, (cm)$ $\Rightarrow BE = \sqrt{AE^{2}+AB^{2}}=\sqrt{10^{2}+15^{2}} \approx 18\, (cm)$

∆BCD vuông tại C

$\Rightarrow BD = \sqrt {B{C^2} + D{C^2}} = \sqrt {{{12}^2} + {{18}^2}} \approx 21,6\,\,cm$ $\Rightarrow BD = \sqrt {B{C^2} + D{C^2}} = \sqrt {{{12}^2} + {{18}^2}} \approx 21,6\,\,cm$

∆EBD vuông tại B

$\Rightarrow ED = \sqrt{EB^{2}+BD^{2}}=\sqrt{325+ 468} \approx 28,2\, (cm)$ $\Rightarrow ED = \sqrt{EB^{2}+BD^{2}}=\sqrt{325+ 468} \approx 28,2\, (cm)$

c) Ta có:

$S_{ABE} + S_{DBC}$ $S_{ABE} + S_{DBC}$

$= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD$ $= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD$

$= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18$ $= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18$

$= 75 + 108 = 183\;cm^2$ $= 75 + 108 = 183\;cm^2$

Ta có: $A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow ACDE$ $A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow ACDE$ là hình thang.

$S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC$ $S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC$

$= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2$ $= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2$

$\Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC}) = 378 - 183 = 195\,cm^2$ $\Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC}) = 378 - 183 = 195\,cm^2$

$S_{EBD}> S_{ABE} + S_{DBC}( 195 > 183)$ $S_{EBD}> S_{ABE} + S_{DBC}( 195 > 183)$

Cách khác:

Các em có thể thay độ dài BE, BD tính được ở câu b để tính diện tích tam giác EBD.

Bài 38 (trang 79 SGK Toán 8 tập 2):

Tính độ dài x, y của các đoạn thẳng trong hình 45.

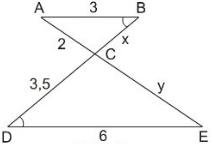
Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Hình 45

Lời giải:

Ta có: $\widehat{ABD} = \widehat{BDE}$ $\widehat{ABD} = \widehat{BDE}$ (gt) mà hai góc ở vị trí so le trong

$\Rightarrow AB // DE$ $\Rightarrow AB // DE$ (dấu hiệu nhận biết hai đường thẳng song song)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

$\Rightarrow ∆ABC ∽ ∆EDC$ $\Rightarrow ∆ABC ∽ ∆EDC$

$\Rightarrow \dfrac{AB}{ED} = \dfrac{BC}{DC} = \dfrac{AC}{EC}$ $\Rightarrow \dfrac{AB}{ED} = \dfrac{BC}{DC} = \dfrac{AC}{EC}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow \dfrac{3}{6} = \dfrac{x}{3,5} = \dfrac{2}{y}$ $\Rightarrow \dfrac{3}{6} = \dfrac{x}{3,5} = \dfrac{2}{y}$

$\Rightarrow x = \dfrac{3. 3,5}{6} = 1,75$ $\Rightarrow x = \dfrac{3. 3,5}{6} = 1,75$

$\Rightarrow y = \dfrac{6.2}{3} = 4$ $\Rightarrow y = \dfrac{6.2}{3} = 4$

Bài 39 (trang 79, 80 SGK Toán 8 Tập 2)

Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.

a) Chứng minh rằng OA.OD = OB.OC

b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.

Chứng minh rằng $\dfrac{OH}{OK} = \dfrac{AB}{CD}$ $\dfrac{OH}{OK} = \dfrac{AB}{CD}$

Lời giải:

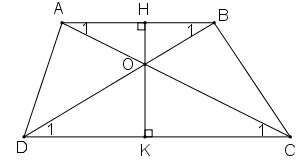
Bài 39

a) Vì AB // \) (giả thiết)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

$\Rightarrow ∆AOB ∽ ∆COD$ $\Rightarrow ∆AOB ∽ ∆COD$

$\Rightarrow \dfrac{OA}{OC} = \dfrac{OB}{OD}$ $\Rightarrow \dfrac{OA}{OC} = \dfrac{OB}{OD}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow OA.OD = OC.OB$ $\Rightarrow OA.OD = OC.OB$

b) Theo câu a) ta có ∆AOB ∽ ∆COD nên $\dfrac{OA}{OC} = \dfrac{AB}{CD}$ $\dfrac{OA}{OC} = \dfrac{AB}{CD}$ (1)

Xét ∆AOH và ∆COK có:

$\widehat{AHO} = \widehat{CKO} = {90^o}$ $\widehat{AHO} = \widehat{CKO} = {90^o}$

$\widehat {HOA} = \widehat {K{\rm{O}}C}$ $\widehat {HOA} = \widehat {K{\rm{O}}C}$ (đối đỉnh)

$\Rightarrow ∆AOH ∽ ∆COK$ $\Rightarrow ∆AOH ∽ ∆COK$ (g-g)

$\Rightarrow \dfrac{OH}{OK}= \dfrac{OA}{OC}$ $\Rightarrow \dfrac{OH}{OK}= \dfrac{OA}{OC}$ (2) (tính chất hai tam giác đồng dạng)

Từ (1) và (2) $\Rightarrow \dfrac{OH}{OK} = \dfrac{AB}{CD}$ $\Rightarrow \dfrac{OH}{OK} = \dfrac{AB}{CD}$

Bài 40 (trang 80 SGK Toán 8 tập 2):

Cho tam giác ABC, trong đó AB = 15cm, AC = 20cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không? Vì sao?

Lời giải:

Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Ta có:

$\frac{AE}{AD}=\frac{6}{8}=\frac{3}{4}$ $\frac{AE}{AD}=\frac{6}{8}=\frac{3}{4}$

$\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}$ $\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}$

$\Rightarrow \frac{AE}{AD} =\frac{AB}{AC}$ $\Rightarrow \frac{AE}{AD} =\frac{AB}{AC}$

Xét ΔAED và ΔABC có:

$\frac{AE}{AD}=\frac{AB}{AC}$ $\frac{AE}{AD}=\frac{AB}{AC}$

Góc A chung

$\Rightarrow$ $\Rightarrow$ ΔAED ∼ ΔABC (Trường hợp thứ 2)

Bài 41 (trang 80 SGK Toán 8 tập 2):

Tìm các dấu hiệu để nhận biết hai tam giác cân đồng dạng.

Lời giải:

Từ trường hợp 1 ta có:

- Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.

Từ trường hợp 2 và 3 ta có:

- Nếu hai tam giác cân có một góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.

Bài 42 (trang 80 SGK Toán 8 tập 2):

36. So sánh các trường hợp đồng dạng của tam giác với các trường hợp bằng nhau của tam giác (nêu lên những điểm giống nhau và khác nhau).

Lời giải:

So sánh:

Trường hợp	Giống nhau	Khác nhau
		Bằng nhau	Đồng dạng
1	3 cạnh	3 cạnh tương ứng bằng nhau	3 cạnh tương ứng tỉ lệ
2	2 cạnh 1 góc	2 cạnh tương ứng và một góc kề với hai cạnh bằng nhau	2 cạnh tương ứng tỉ lệ
3	2 góc bằng nhau	1 cạnh và 2 góc kề tương ứng bằng nhau	Chỉ 2 góc bằng nhau, không cần có điều kiện cạnh

Bài 43 (trang 80 SGK Toán 8 tập 2):

Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F.

a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.

b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE = 10cm.

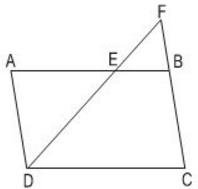
Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

Hình 46

Lời giải:

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.

BE // DC (vì ABCD là hình bình hành) $\Rightarrow ∆BFE ∽ ∆CFD$ $\Rightarrow ∆BFE ∽ ∆CFD$ (1)

AD // BF (vì ABCD là hình bình hành) $\Rightarrow ∆ADE ∽ ∆BFE$ $\Rightarrow ∆ADE ∽ ∆BFE$ (2)

Từ (1) và (2) suy ra ∆ADE ∽ ∆CFD

b) Ta có: BE = AB - AE = 12 - 8 = 4cm; AD=BC=7cm (vì ABCD là hình bình hành)

Ta có: ∆ADE ∽ ∆BFE (cmt)

$\Rightarrow \dfrac{AE}{BE} = \dfrac{AD}{BF} = \dfrac{DE}{EF}$ $\Rightarrow \dfrac{AE}{BE} = \dfrac{AD}{BF} = \dfrac{DE}{EF}$ (tính chất tam giác đồng dạng)

$\Rightarrow \dfrac{8}{4} = \dfrac{7}{BF} = \dfrac{10}{EF}$ $\Rightarrow \dfrac{8}{4} = \dfrac{7}{BF} = \dfrac{10}{EF}$

$\eqalign{ & \Rightarrow BF = {{4.7} \over 8} = 3,5\,cm \cr & \Rightarrow EF = {{10.4} \over 8} = 5\,cm \cr}$ $\eqalign{ & \Rightarrow BF = {{4.7} \over 8} = 3,5\,cm \cr & \Rightarrow EF = {{10.4} \over 8} = 5\,cm \cr}$

Bài 44 (trang 80 SGK Toán 8 tập 2):

Cho tam giác ABC có các cạnh AB = 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.

a) Tính tỉ số $\frac{BM}{CN}$ $\frac{BM}{CN}$

b) Chứng minh rằng $\frac{AM}{AN}=\frac{DM}{DN}$ $\frac{AM}{AN}=\frac{DM}{DN}$

Lời giải:

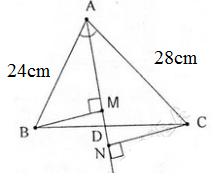
Giải bài tập SGK Toán lớp 8 bài 7: Trường hợp đồng dạng thứ ba

a) AD là đường phân giác trong ΔABC

$\Rightarrow \frac{DB}{DC}=\frac{AB}{AC}\Rightarrow \frac{DB}{DC}=\frac{24}{28}=\frac{6}{7}$ $\Rightarrow \frac{DB}{DC}=\frac{AB}{AC}\Rightarrow \frac{DB}{DC}=\frac{24}{28}=\frac{6}{7}$

Mà BM song song CN (Cùng vuông góc với AD)

$\Rightarrow$ $\Rightarrow$ ΔBMD ∼ ΔCND

$\Rightarrow \frac{BM}{CN} = \frac{BD}{CD}$ $\Rightarrow \frac{BM}{CN} = \frac{BD}{CD}$

$\Rightarrow \frac{BM}{CN}=\frac{6}{7}$ $\Rightarrow \frac{BM}{CN}=\frac{6}{7}$

b) ΔABM và ΔACN có góc BAM = góc CAN (AD là phân giác góc BAC)

Góc BMA = Góc CNA = 90^o

Suy ra ΔABM ∼ ΔACN

^{$\Rightarrow\frac{AM}{AN}=\frac{AB}{AC}$}

Mà^{$\frac{AB}{AC}=\frac{DB}{DC}$}(chứng minh trên)

và^{$\frac{DB}{DC}=\frac{DM}{DN}$}(ΔBMD ∼ ΔCND)

^{$\Rightarrow \frac{AM}{AN} = \frac{DM}{DN}$}

Bài 45 (trang 80 SGK Toán 8 tập 2):

Hai tam giác ABC và DEF có góc A = góc D, góc B = góc E, AB = 8cm, BC = 10cm, DE =6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.

Lời giải:

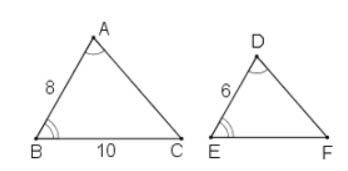
Bài 45

Xét ∆ABC và ∆DEF có:

$\widehat{A} = \widehat{D}$ $\widehat{A} = \widehat{D}$ (giả thiết)

$\widehat{B} = \widehat{E}$ $\widehat{B} = \widehat{E}$ (giả thiết)

$\Rightarrow ∆ABC ∽ ∆DEF (g - g)$ $\Rightarrow ∆ABC ∽ ∆DEF (g - g)$

$\Rightarrow \dfrac{AB}{DE}= \dfrac{BC}{EF} = \dfrac{CA}{FD}$ $\Rightarrow \dfrac{AB}{DE}= \dfrac{BC}{EF} = \dfrac{CA}{FD}$ (tính chất hai tam giác đồng dạng)

Hay $\dfrac{8}{6} = \dfrac{10}{EF} = \dfrac{CA}{FD}$ $\dfrac{8}{6} = \dfrac{10}{EF} = \dfrac{CA}{FD}$

Suy ra: $EF = 6.10 : 8 = 7,5 cm$

Vì $\dfrac{8}{6} = \dfrac{CA}{FD}$ $\dfrac{8}{6} = \dfrac{CA}{FD}$

$\Rightarrow \dfrac{CA}{8} = \dfrac{FD}{6} = \dfrac{CA - FD}{8-6}= \dfrac{3}{2}$ $\Rightarrow \dfrac{CA}{8} = \dfrac{FD}{6} = \dfrac{CA - FD}{8-6}= \dfrac{3}{2}$ (Tính chất của dãy tỉ số bằng nhau).

$\Rightarrow CA = \dfrac{8.3}{2} = 12 cm$ $\Rightarrow CA = \dfrac{8.3}{2} = 12 cm$

$FD = 12 -3 = 9cm$

.............................

Trên đây, VnDoc đã gửi tới các bạn Giải Toán 8 bài 7: Trường hợp đồng dạng thứ ba. Trong quá trình học môn Toán lớp 8, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã sưu tầm và chọn lọc thêm phần Giải Toán 8 hay Giải Vở BT Toán 8 để giúp các bạn học sinh học tốt hơn.

Ngoài bài tập cơ bản môn Toán lớp 8 chuyên đề này, các bạn học sinh có thể tham khảo thêm các đề thi học kì 2 môn Toán, môn Ngữ Văn, chuẩn bị tốt kiến thức cho kì thi học kì 2 sắp tới.

Chia sẻ, đánh giá bài viết

7

9.137

Bài trước

Bài sau