Giải Toán 8 bài 1: Định lí Ta-lét trong tam giác
Giải bài tập Toán lớp 8 bài 1: Định lí Ta-lét trong tam giác
- Câu hỏi 1 trang 56 SGK Toán 8 tập 2
- Câu hỏi 2 trang 57 SGK Toán 8 tập 2
- Câu hỏi 3 trang 57 SGK Toán 8 tập 2
- Câu hỏi 4 trang 58 SGK Toán 8 tập 2
- Bài 1 (trang 58 SGK Toán 8 tập 2):
- Bài 2 (trang 59 SGK Toán 8 Tập 2)
- Bài 3 (trang 59 SGK Toán 8 tập 2):
- Bài 4 (trang 59 SGK Toán 8 Tập 2)
- Bài 5 (trang 59 SGK Toán 8 tập 2):
Giải SGK Toán 8 bài 1: Định lí Ta-lét trong tam giác với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Hướng dẫn giải: hay bài tập Toán 8 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.
- Giải bài tập SGK Toán lớp 8 bài 4: Bất phương trình bậc nhất một ẩn
- Giải bài tập SGK Toán lớp 8 bài 5: Phương trình chứa dấu giá trị tuyệt đối
- Giải bài tập SGK Toán lớp 8 bài: Ôn tập chương IV- Bất phương trình bậc nhất một ẩn
Câu hỏi 1 trang 56 SGK Toán 8 tập 2
Cho AB = 3cm; CD = 5cm, 
\(\frac{AB}{CD}=?\)
EF = 4dm, MN = 7dm, \(\frac{EF}{MN}=?\)
Hướng dẫn giải:
\(\frac{AB}{CD}=\frac{3}{5}\)
\(\frac{EF}{MN}=\frac{4}{7}\)
Câu hỏi 2 trang 57 SGK Toán 8 tập 2
Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ (h.2). So sánh các tỉ số: \(\frac{AB}{CD}\) và \(\frac{A'B'}{C'D'}\)
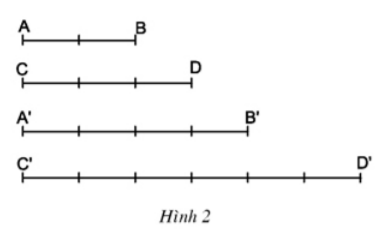
Hướng dẫn giải:
\(\frac{AB}{CD}=\frac{2}{3}\)
\(\frac{A'B'}{C'D'}=\frac{4}{6}\Rightarrow \frac{A'B'}{C'D'}=\frac{2}{3}\)
Vậy \(\frac{AB}{CD}=\frac{A'B'}{C'D'}\)
Câu hỏi 3 trang 57 SGK Toán 8 tập 2
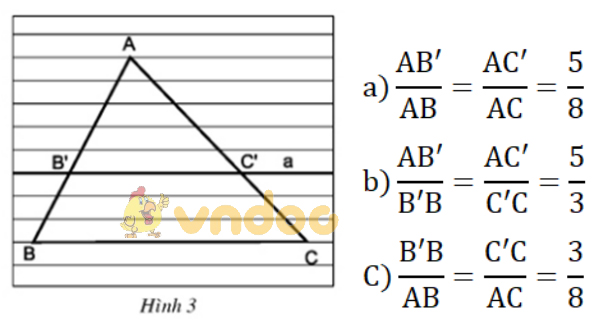
Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B' và C'.
Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB', B'B và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC', C'C và AC.
So sánh các tỉ số:
Hướng dẫn giải:
Câu hỏi 4 trang 58 SGK Toán 8 tập 2
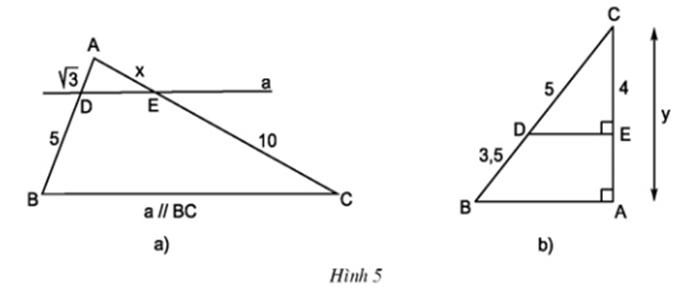
Tính các độ dài x và y trong hình 5.
Hướng dẫn giải:
Xét hình 5a.
Theo bài ra có: a // BC áp dụng định lý Ta – lét trong tam giác ta có:
\(\begin{align}
& \frac{AD}{BD}=\frac{AE}{EC} \\
& \Rightarrow \frac{\sqrt{3}}{5}=\frac{x}{10} \\
& \Rightarrow x=\frac{10.\sqrt{3}}{5}=2\sqrt{3} \\
\end{align}\)
Xét hình 5b.
Ta có: \(\left\{ \begin{matrix}
DE\bot CA \\
AB\bot CA \\
\end{matrix}\Rightarrow DE//AB \right.\) áp dụng định lý Ta – lét trong tam giác ta có:
\(\begin{align}
& \frac{DC}{BC}=\frac{CE}{CA} \\
& \Rightarrow \frac{DC}{DC+BD}=\frac{CE}{CA} \\
& \Rightarrow \frac{5}{5+3,5}=\frac{4}{y} \\
& \Rightarrow \frac{5}{8,5}=\frac{4}{y}\Rightarrow y=\frac{4.8,5}{5}=6,8 \\
\end{align}\)
Bài 1 (trang 58 SGK Toán 8 tập 2):
Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
(Ghi nhớ (định nghĩa trang 56 sgk Toán 8 Tập 2)
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.)
Hướng dẫn giải:
a) Ta có AB = 5cm và CD = 15 cm
\(\Rightarrow \dfrac{AB}{CD}= \dfrac{5}{15}= \dfrac{1}{3}\)
b) EF= 48 cm, GH = 16 dm = 160 cm
\(\Rightarrow \dfrac{EF}{GH}= \dfrac{48}{160}= \dfrac{3}{10}\)
c) PQ= 1,2m = 120cm, MN= 24cm
\(\Rightarrow \dfrac{PQ}{MN} = \dfrac{120}{24} = 5\)
Bài 2 (trang 59 SGK Toán 8 Tập 2)
Cho biết \(\dfrac{AB}{CD} = \dfrac{3}{4}\)
và CD= 12cm. Tính độ dài AB.
Hướng dẫn giải:
Ta có: \(\dfrac{AB}{CD} = \dfrac{3}{4}\) mà CD= 12cm nên
\(\dfrac{AB}{12}=\dfrac{3}{4}\)
\(\Rightarrow AB= \dfrac{12.3}{4} = 9cm\)
Vậy AB = 9cm.
Bài 3 (trang 59 SGK Toán 8 tập 2):
Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.
Hướng dẫn giải:
Độ dài AB gấp 5 lần độ dài CD nên AB= 5CD.
Độ dài A'B' gấp 12 lần độ dài CD nên A'B'= 12CD.
\(\Rightarrow\) Tỉ số của hai đoạn thẳng AB và A'B' là:
\(\dfrac{AB}{A'B'}= \dfrac{5CD}{12CD} = \dfrac{5}{12}\)
Bài 4 (trang 59 SGK Toán 8 Tập 2)
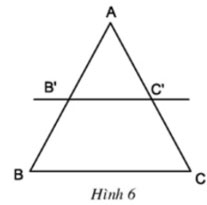
Cho biết \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) (h.6)
Chứng minh rằng:
a) \(\dfrac{AB'}{B'B}= \dfrac{AC'}{C'C}\)
b) \(\dfrac{BB'}{AB}= \dfrac{CC'}{AC}\)
Hướng dẫn: Áp dụng tính chất của tỉ lệ thức.
a) Ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) (giả thiết)
\(\Rightarrow \dfrac{AC}{AC'}=\dfrac{AB}{AB'}\)
\(\Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1\)
Ta có:
\(\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}\)
\(\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}\)
\(\Rightarrow \dfrac{{C'C}}{{AC'}} = \dfrac{{B'B}}{{AB'}} \Rightarrow \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) (điều phải chứng minh).
b) Vì \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\)
Mà \(AB' = AB - B'B, AC' = AC - C'C\)
\(\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}\)
\(\Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}\)
\(\Rightarrow \dfrac{BB'}{AB}= \dfrac{CC'}{AC}\) (điều phải chứng minh).
Bài 5 (trang 59 SGK Toán 8 tập 2):
Tính x trong các trường hợp sau (h.7):
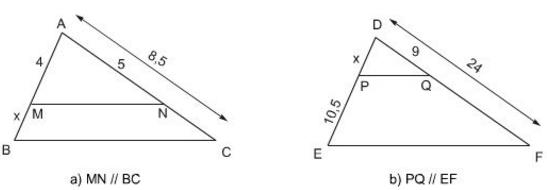
Hướng dẫn giải:
a) MN // BC (giả thiết)
Theo định lí Ta-lét ta có:
\(\dfrac{BM}{AM} = \dfrac{CN}{AN}\)
Mà CN =AC- AN= 8,5 - 5= 3,5
nên \(\dfrac{x}{4}= \dfrac{3,5}{5} \Rightarrow x = \dfrac{4.3,5}{5} = 2,8\)
Vậy x = 2,8.
b) PQ // EF (giả thiết)
Theo định lí Ta-lét ta có:
\(\dfrac{DP}{PE} = \dfrac{DQ}{QF}\)
Mà QF = DF - DQ = 24 - 9 = 15
Nên \(\dfrac{x}{10,5} = \dfrac{9}{15} \Rightarrow x = \dfrac{10,5.9}{15} = 6,3\)
Vậy x=6,3.
Ngoài Giải bài tập SGK Toán lớp 8 bài 1: Định lí Ta-lét trong tam giác, các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.
