Giải bài tập SBT Toán 8 bài: Ôn tập chương II

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài: Ôn tập chương 2 được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 5: Diện tích hình thoi

Giải bài tập SBT Toán 8 bài 6: Diện tích đa giác

Giải bài tập SBT Toán 8 bài 1: Định lí Ta-lét trong tam giác

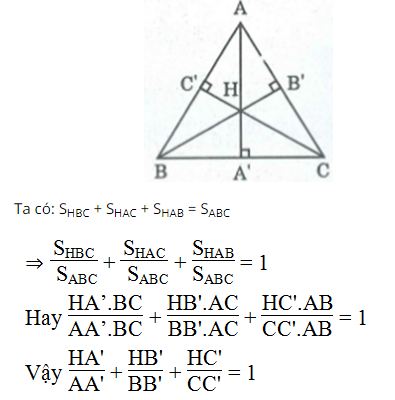
Câu 1: Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chứng minh rằng

Lời giải

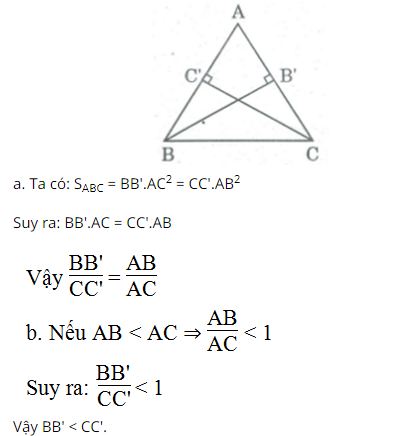
Câu 2: Cho tam giác ABC.

a, Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C

b, Tại sao nếu AB < AC thì BB' < CC’

Lời giải:

Câu 3: Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thắng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo).

Lời giải:

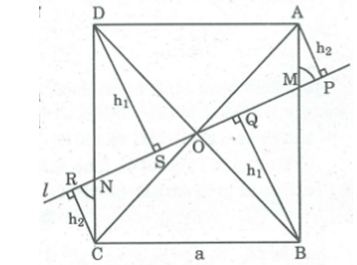
Gọi h1 và h2 là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l

Tổng khoảng cách là S.

Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)

Suy ra AM = CN

Mà: ∠(AMP) = ∠(DNS) (đồng vị)

∠(DNS) = ∠(CNR) (đôi đỉnh)

Suy ra: ∠(AMP) = ∠(CNR)

Suy ra: ΔAPM = ΔCRN (cạnh huyền, góc nhọn)

⇒ CR = AP = h2

AM = CD ⇒ BM = DN

∠(BMQ) = ∠(DNS) (so le trong)

Suy ra: ΔBQM = ΔDSN (cạnh huyền, góc nhọn) ⇒ DS = BQ = h1

S_BOA = 1/4 S_AOB = 1/4 a² (l)

S_BOA = S_BOM + S_AOM = 1/2 .b/2 .h1 + 1/2 .b/2 .h2

Từ (1) va (2) suy ra h1 + h2 = a2b . Vậy : S = 2(h1 + h2) = 2a²b

Câu 4: Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN.

Lời giải:

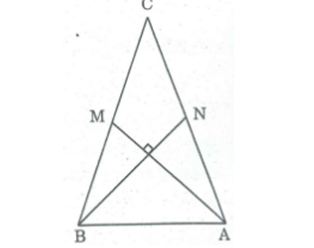
Tứ giác ẠBMN có hai đường chéo vuông góc.

Ta có: S_ABMN = 1/2 AM.BN

Δ ABM và Δ AMC có chung chiều cao kể từ A, cạnh đáy BM = MC nên: S_ABM = S_AMC = 1/2 SABC

ΔMNA và ΔMNC có chung chiều cao kê từ M, cạnh đáy AN = NC nên: S_MAN = S_MNC = 1/2 SAMC = 1/4 SABC

S_ABMN = S_ABM + S_MNA = 1/2 SABC + 1/4 SABC = 3/4 SABC

Vậy S_ABC = 4/3 S_ABMN = 4/3 .1/2 .AM.BN = 2/3 AM.BN

Câu 5: Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC.

a, Tính các góc B, C, cạnh AC và diện tích tam giác ABC.

b, Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.

c, Tính diện tích tứ giác DEFCL

Lời giải:

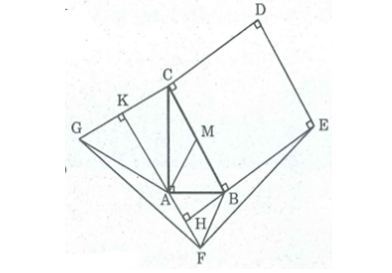
a, Gọi M là trung điểm của BG, ta có:

AM = MB = 1/2 BC = a (tính chất tam giác vuông)

Suy ra MA = MB = AB = a

Suy ra ΔAMB đều ⇒ ∠(ABC) = 60^o

Mặt khác: ∠(ABC) = ∠(ACB) (tính chất tam giác vuông)

Suy ra: ∠(ACB) = 90^o - ∠(ABC) = 90^o – 60o = 30^o

Trong tam giác vuông ABC, theo Pi-ta-go, ta có: BC² = AB²+ AC²

⇒ AC² = BC² - AB² = 4a² - a² = 3a² ⇒ AC = a√3

Vậy SABC = 1/2 .AB.AC =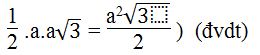

b, Ta có: ∠(FAB) = ∠(ABC) = 60^o

FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

BC ⊥ BE (vì BCDE là hình vuông)

Suy ra: FA ⊥ BE

BC ⊥ CD (vì BCDE là hình vuông)

Suy ra: FA ⊥ CD

Gọi giao điểm BE và FA là H, FA và CG là K.

⇒ BH ⊥ FA và FH = HA = a2 (tính chất tam giác đều)

∠(ACG) + ∠(ACB) + ∠(BCD) = 60^o + 30^o + 90^o = 180^o

⇒ G, C, D thẳng hàng

⇒ AK ⊥ CG và GK = KC = 1/2 GC = 1/2 AC = (a√3)/2