Giải bài tập SBT Toán 8 bài: Ôn tập chương III
Bài tập môn Toán lớp 8
Giải bài tập SBT Toán 8 bài: Ôn tập chương 3 được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Giải bài tập SBT Toán 8 bài 7: Trường hợp đồng dạng thứ ba (g.g)
Giải bài tập SBT Toán 8 bài 8: Các trường hợp đồng dạng của tam giác vuông
Giải bài tập SBT Toán 8 bài 1: Hình hộp chữ nhật
Câu 1: Tứ giác ABCD có hai góc vuông tại đỉnh A và C hai đường chéo AC và BD cắt nhau tại O ,(BAO) = (BDC) .Chứng minh:
a, ΔABO đồng dạng ΔDCO
b, ΔBOC đồng dạng ΔADO
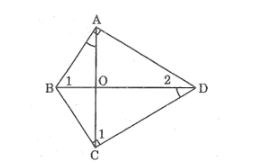
Lời giải:
Xét ΔABO và ΔDCO,ta có:
∠(BAO) = ∠(BDC) (gt)
Hay ∠(BAO) = ∠(ODC)
∠(AOB) = ∠(DOC) (đối đỉnh)
Vậy ΔABO đồng dạng ΔDCO (g.g)
b, Vì ΔABO đồng dạng ΔDCO nên:
∠(B1) = ∠(C1) (1)
Mà ∠(C1) + ∠(C2) = ∠(BCD) = 90o (2)
Trong ΔABD, ta có: ∠A = 90o
Suy ra: ∠(B1) + ∠(D2) = 90o (3)
Từ (1), (2) và (3): Suy ra: ∠(C2) = ∠(D2)
Xét ΔBCO và ΔADO, ta có:
∠(C2) = ∠(D2) (chứng minh trên)
∠(BOC) = ∠(AOD) (đối đỉnh)
Vậy ΔBOC đồng dạng ΔADO (g.g).
Câu 2: Cho hình chữ nhật ABCD có AB = a = 12cm, BG = b = 9m. Gọi H là chân đường vuông góc kẻ từ A xuống BD
a, Chứng minh ΔAHB đồng dạng ΔBCD
b, Tính độ dài đoạn thắng AH
c, Tính diện tích tam giác AHb,
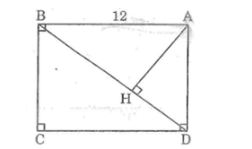
Lời giải:
Xét ΔAHB và. ΔBCD, ta có:
∠(AHB) = ∠(BCD) =90o
AB // CD (gt)
∠(ABH) = ∠(BDC) (so le trong)
Vậy ΔAHB đồng dạng ΔBCD (g.g)
Vì ΔAHB đồng dạng ΔBCD nên:
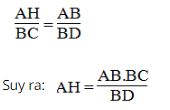
Áp dụng định lí Pi-ta-go vào tam giác vuông BCD,ta có:
BD2 = BC2 + CD2 = BC2 + AB2
= 122 + 92 = 225
Suy ra: BD = 15cm
Vậy AH = (12.9)/15 = 7,2 cm
Vì ΔAHB đồng dạng ΔBCD nên AH/BC = (7.2)/9 = 0,8
Ta có: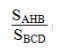 
= k2 = (0,8)2 = 0,64 ⇒ SAHB = 0,64SBCD
SBCD = 1/2 BC.CD = 1/2 .12.9 = 54(cm2)
Vậy SAHB = 0,64.SBCD = 0,64.54 = 34,56 (cm2).
Câu 3: Tứ giác ABCD có hai dường chéo AC và BD cắt nhau tại O, ∠(ABD) = ∠(ACD) . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:
a, ΔAOB đồng dạng ΔDOC
b, ΔẠOD đồng dạng ΔBOC
c, Ea, ED = Eb, EC.
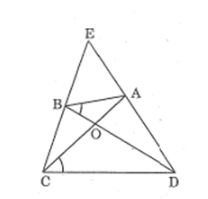
Lời giải:
Xét ΔAOB và ΔDOC, ta có:
∠(ABD) = ∠(ACD) (gt)
Hay ∠(ABO) = ∠(OCD)
∠(AOB) = ∠(DOC) (đối đỉnh)
Vậy ΔAOB đồng dạng ΔDOC (g.g)
Vì ΔAOB đồng dạng ΔDOC nên:
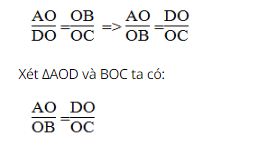
∠(AOD) = ∠(BOC) (đối đỉnh)
Vậy ΔAOD đồng dạng ΔBOC (c.g.c)
Vì ΔAOD đồng dạng ΔBOC nên: ∠(ADC) = ∠(BCO) hay ∠(EDB) = ∠(ECA)
Xét ΔEDB và ΔECA ta có:
∠E chung
∠(EDB) = ∠(ECA) (chứng minh trên)
Vậy ΔEDB đồng dạng ΔECA(g.g)
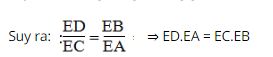
Câu 4: Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH
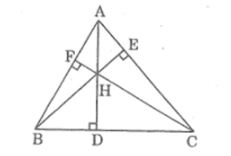
Lời giải:
Xét ΔAFH và ΔCDH, ta có:
∠(AFH) = ∠(CDH) = 90o
∠(AHF) = ∠(CHD) (đối đỉnh)
Suy ra: ΔAFH đồng dạng ΔCDH (g.g)
Suy ra: AH/CH = FH/DH
Suy ra: AH.DH = CH.FH (1)
Xét ΔAEH và ΔBDH,ta có:
∠(AEH) = ∠(BDH) = 90o
∠(AHE) = ∠(BHD) (đối đỉnh)
Suy ra: ΔAEH đồng dạng ΔBDH (g.g)
Suy ra: AH/BH = EH/DH
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.
Câu 5: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng Ab, AE + AD.AF = AC2
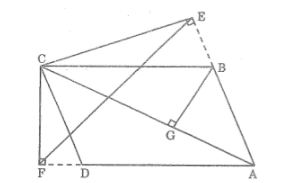
Lời giải:
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠(BGA) = ∠(CEA) = 90o
∠A chung
⇒ΔBGA đồng dạng ΔCEA(g.g)
Suy ra: AB/AC = AG/AE
Ab, AE = AC.AG (1)
Xét ΔBGC và ΔCFA, ta có:
∠(BGC) = ∠(CFA) = 90o
∠(BCG) = ∠(CAF) (so le trong vì AD //BC)
ΔBGC đồng dạng ΔCFA (g.g)
Suy ra: AF/CG = AC/BC ⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
Ab, AE + AD.AF = AC.AG + AC.CG
Ab, AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên Ab, AE + AD.AF = AC2.
Câu 6: Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.
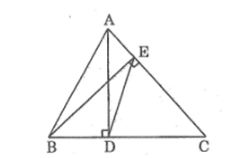
Lời giải:
Xét ΔADC và ΔBEC, ta có:
∠(ADC) =∠(BEC) = 90o
∠C chung
Suy ra: ΔADC đồng dạng ΔBEC (g.g)
