Giải Toán 8 bài 1: Mở đầu về phương trình - Luyện tập
Giải bài tập Toán 8 trang 5, 6, 7 tập 2
VnDoc xin giới thiệu cho các bạn bài Giải Toán 8 bài 1: Mở đầu về phương trình - Luyện tập nhằm giúp các bạn học sinh rèn luyện, nâng cao kỹ năng giải toán 8. Chúc các bạn đạt điểm cao trong kì thi sắp tới.
Câu hỏi 1 Trang 5 SGK Toán 8 tập 2
Hãy cho ví dụ về:
a) Phương trình với ẩn y.
b) Phương trình với ẩn u.
Hướng dẫn giải:
a) Phương trình với ẩn y: 15y + 1 = 16
b) Phương trình với ẩn u: 2u – 11 = 3(u+1)
Câu hỏi 2 Trang 5 SGK Toán 8 tập 2
Khi x = 6, tính giá trị mỗi vế của phương trình: 2x + 5 = 3(x – 1) + 2.
Hướng dẫn giải:
Khi x= 6, ta có:
VT = 2x + 5 = 2.6 + 5 = 12 + 5 = 17
VP = 3(x – 1) + 2 = 3(6– 1) + 2 = 3.5 + 2 = 15 + 2 = 17
Câu hỏi 3 Trang 5 SGK Toán 8 tập 2
Cho phương trình 2(x + 2) – 7 = 3 – x
a) x = - 2 có thỏa mãn phương trình không ?
b) x = 2 có là một nghiệm của phương trình không ?
Hướng dẫn giải:
a) Tại x = -2 ta có:
Vế trái = 2(x + 2) – 7 = 2(– 2 + 2) – 7 = 2.0 – 7 = –7.
Vế phải = 3 – x = 3 – (– 2) = 5.
Vì 5 ≠ –7 nên vế trái ≠ vế phải suy ra x = – 2 không thỏa mãn phương trình.
Vậy x = – 2 không thỏa mãn phương trình.
b)Tại x = 2 ta có:
Vế trái = 2(2 + 2) – 7 = 2.4 – 7 = 8 – 7 = 1
Vế phải = 3 – x = 3 – 2 = 1
⇒ vế trái = vế phải = 1 nên x = 2 là một nghiệm của phương trình.
Vậy x = 2 là một nghiệm của phương trình.
Câu hỏi 3 Trang 6 SGK Toán 8 tập 2
Hãy điền vào chỗ trống (…):
a) Phương trình x = 2 có tập nghiệm là S = …
b) Phương trình vô nghiệm có tập nghiệm là S = …
Hướng dẫn giải:
a) Phương trình x = 2 có tập nghiệm là S = {2}
b) Phương trình vô nghiệm có tập nghiệm là S = ∅
Bài 1 (trang 6 SGK Toán 8 Tập 2)
Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không?
a) 4x - 1 = 3x - 2; b) x + 1 = 2(x - 3); c) 2(x + 1) + 3 = 2 - x?
Hướng dẫn giải:
a) 4x - 1 = 3x - 2
Vế trái: 4x - 1 = 4(-1) - 1 = -5
Vế phải: 3x - 2 = 3(-1) -2 = -5
=> Vì vế trái bằng vế phải nên x = -1 là nghiệm của phương trình.
b) x + 1 = 2(x - 3)
Vế trái: x + 1 = -1 + 1 = 0
Vế phải: 2(x - 3) = 2(-1 - 3) = -8
=> Vì VT ≠ VP nên x = -1 không là nghiệm của phương trình.
c) 2(x + 1) + 3 = 2 - x?
Vế trái: 2(x + 1) + 3 = 2(-1 + 1) + 3 = 3
Vế phải: 2 - x = 2 - (-1) = 3
=> Vì vế trái bằng vế phải nên x = -1 là nghiệm của phương trình
Bài 2 (trang 6 SGK Toán 8 Tập 2)
Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình.
(t + 2)2 = 3t + 4
Hướng dẫn giải:
- Với t = -1
VT = (t + 2)2 = (-1 + 2)2 = 1
VP = 3t + 4 = 3(-1) + 4 = 1
=> Vì vế trái bằng vế phải nên t = -1 là nghiệm của phương trình
- Với t = 0
VT = (t + 2)2 = (0 + 2)2 = 4
VP = 3t + 4 = 3.0 + 4 = 4
=> Vì vế trái bằng vế phải nên t = 0 là nghiệm của phương trình
- Với t = 1
VT = (t + 2)2 = (1 + 2)2 = 9
VP = 3t + 4 = 3.1 + 4 = 7
=> Vì vế trái khác vế phải nên t = 1 không là nghiệm của phương trình.
Bài 3 (trang 6 SGK Toán 8 Tập 2)
Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.
Hướng dẫn giải:
=> Vì phương trình x + 1 = 1 + x nghiệm đúng với mọi x ε R. Vậy tập hợp nghiệm của phương trình trên là: S = {x ε R}
Bài 4 (trang 7 SGK Toán 8 Tập 2)
Nối mỗi phương trình sau với các nghiệm của nó:
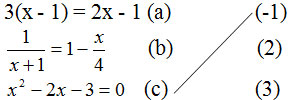
Hướng dẫn giải:
+ Xét phương trình (a): 3(x – 1) = 2x – 1
Tại x = -1 có:
VT = 3(x – 1) = 3(-1 – 1) = -6;
VP = 2x – 1 = 2.(-1) – 1 = -3.
⇒ -6 ≠ -3 nên -1 không phải nghiệm của phương trình (a).
Tại x = 2 có:
VT = 3(x – 1) = 3.(2 – 1) = 3;
VP = 2x – 1 = 2.2 – 1 = 3
⇒ VT = VP = 3 nên 2 là nghiệm của phương trình (a).
Tại x = 3 có:
VT = 3(x – 1) = 3.(3 – 1) = 6;
VP = 2x – 1 = 2.3 – 1 = 5
⇒ 6 ≠ 5 nên 3 không phải nghiệm của phương trình (a).
+ Xét phương trình (b): 
\(\dfrac{1}{{x + 1}} = 1 - \dfrac{x}{4}\;\;\;\;\;\)
Tại x = -1, biểu thức \(\dfrac{1}{{x + 1}}\) không xác định
⇒ -1 không phải nghiệm của phương trình (b)
Tại x = 2 có:
\(\eqalign{ & VT = {1 \over {2 + 1}} = {1 \over 3} \cr & VP = 1 - {2 \over 4} = 1 - {1 \over 2} = {1 \over 2} \cr}\)
⇒ Do \(\frac{1}{3} ≠\frac{1}{2}\) nên 2 không phải nghiệm của phương trình (b).
Tại x = 3 có:
\(\eqalign{ & VT = {1 \over {3 + 1}} = {1 \over 4} \cr & VP = 1 - {3 \over 4} = {4 \over 4} - {3 \over 4} = {1 \over 4} \cr}\)
⇒ \(VT=VP=\frac{1}{4}\) nên 3 là nghiệm của phương trình (b).
+ Xét phương trình (c) : x2 – 2x – 3 = 0
Tại x = -1 có: VT = x2 – 2x – 3 = (-1)2 – 2.(-1) – 3 = 0 = VP
⇒ x = -1 là nghiệm của phương trình x2 – 2x – 3 = 0
Tại x = 2 có: x2 – 2x – 3 = 22 – 2.2 – 3 = -3 ≠ 0.
⇒ x = 2 không phải nghiệm của phương trình x2 – 2x – 3 = 0.
Tại x = 3 có: x2 – 2x – 3 = 32 – 2.3 – 3 = 0
⇒ x = 3 là nghiệm của phương trình x2 – 2x – 3 = 0.
Vậy ta có thể nối như sau:
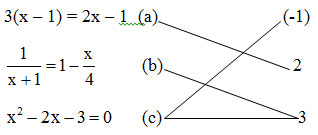
Bài 5 (trang 7 SGK Toán 8 Tập 2)
Hai phương trình x = 0 và x(x - 1) = 0 có tương đương không? Vì sao?
Hướng dẫn giải:
Phương trình x = 0 có tập nghiệm S1 = {0}.
Xét phương trình x(x - 1) = 0. Vì một tích bằng 0 khi mọt trong hai thừa số bằng 0 tức là: x = 0 hoặc x = 1
Vậy phương trình x(x - 1) = 0 có tập nghiệm S2 = {0;1}
=> Vì S1 # S2 nên hai phương trình không tương đương.
..................................
Trên đây VnDoc đã giới thiệu tới các bạn Giải Toán 8 bài 1: Mở đầu về phương trình - Luyện tập. Hy vọng đây là tài liệu hay giúp các em nâng cao kỹ năng giải Toán 8 và học tốt môn Toán lớp 8 hơn.
Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
