Mở đầu về phương trình
Chuyên đề Toán học lớp 8: Mở đầu về phương trình được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Mở đầu về phương trình
A. Lý thuyết
1. Phương trình một ẩn
+ Một phương trình với ẩn x là hệ thức có dạng A(x) = B(x), trong đó A(x) gọi là vế trái, B(x) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
Chú ý:
Hệ thức x = m (với m là một số nào đó) cũng là một phương trình. Phương trình này chỉ rõ rằng m là nghiệm duy nhất của nó.
Một phương trình có thể có một nghiệm, hai nghiệm, ba nghiệm,….nhưng cũng có thể không có nghiệm nào hoặc có vô số nghiệm. Phương trình không có nghiệm nào được gọi là phương trình vô nghiệm.
Ví dụ 1:
3x + 2 = 2x là phương trình với ẩn x.
2y - 1 = 4(1 - y) + 3 là phương trình với ẩn y.
Ví dụ 2:
Phương trình x2 = 1 có hai nghiệm x = 1 và x = - 1.
Phương trình x2 = - 1 vô nghiệm
2. Giải phương trình
+ Giải phương trình là tìm tất cả các nghiệm của phương trình.
+ Tìm tập hợp tất cả các nghiệm của một phương trình được gọi là tập nghiệm của phương trình đó. Tập hợp các nghiệm của phương trình kí hiệu là S.
Ví dụ:
Phương trình x = 3 có tập nghiệm là S = {3}.
Phương trình vô nghiệm có tập nghiệm là![]()
3. Phương trình tương đương.
Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.
Kí hiệu ⇔ đọc là tương đương.
Ví dụ:
x + 3 = 0 ⇔ x = - 3.
x - 1 = 3 ⇔ x = 4.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Trong các phương trình sau, phương trình nào là phương trình một ẩn?
A. 2x = x + 1.
B. x + y = 3x.
C. 2a + b = 1.
D. xyz = xy.
+ Một phương trình với ẩn x là hệ thức có dạng A(x) = B(x), trong đó A(x) gọi là vế trái, B(x) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
Nhận xét:
+ Đáp án A: là phương trình một ẩn là x
+ Đáp án B: là phương trình hai ẩn là x,y
+ Đáp án C: là phương trình hai ẩn là a,b
+ Đáp án D: là phương trình ba ẩn là x,y,z
Chọn đáp án A.
Bài 2: Nghiệm x = - 4 là nghiệm của phương trình?
A. - 2,5x + 1 = 11.
B. - 2,5x = - 10
C. 3x - 8 = 0
D. 3x - 1 = x + 7
+ Đáp án A: - 2,5x + 1 = 11 ⇔ - 2,5x = 10 ⇔ x = 10/ - 2,5 = - 4 → Đáp án A đúng.
+ Đáp án B: - 2,5x = - 10 ⇔ x = - 10/ - 0,25 = 4 → Đáp án B sai.
+ Đáp án C: 3x - 8 = 0 ⇔ 3x = 8 ⇔ x = 8/3 → Đáp án C sai.
+ Đáp án D: 3x - 1 = x + 7 ⇔ 3x - x = 7 + 1 ⇔ 2x = 8 ⇔ x = 4 → Đáp án D sai.
Chọn đáp án A.
Bài 3: Trong các phương trình sau, cặp phương trình nào tương đương?
A. x = 1 và x(x - 1) = 0
B. x - 2 = 0 và 2x - 4 = 0
C. 5x = 0 và 2x - 1 = 0
D. x2 - 4 = 0 và 2x - 2 = 0
Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.
Đáp án A:
+ Phương trình x = 1 có tập nghiệm S = {1}
+ Phương trình x(x - 1) = 0 ⇔ có tập nghiệm là S = {0;1}
→ Hai phương trình không tương đương.
Đáp án B:
+ Phương trình x - 2 = 0 có tập nghiệm S = {2}
+ Phương trình 2x - 4 = 0 có tập nghiệm là S = {2}
→ Hai phương trình tương đương.
Đáp án C:
+ Phương trình 5x = 0 có tập nghiệm là S = {0}
+ Phương trình 2x - 1 = 0 có tập nghiệm là S = {1/2}
→ Hai phương trình không tương đương.
Đáp án D:
+ Phương trình x2 - 4 = 0 ⇔ x = ± 2 có tập nghiệm là S = {± 2}
+ Phương trình 2x - 2 = 0 có tập nghiệm là S = {1}
→ Hai phương trình không tương đương.
Chọn đáp án B.
Bài 4: Tập nghiệm của phương trình 3x - 6 = 0 là?
A. S = {1}
B. S = {2}
C. S = {- 2}
D. S = {1}
Ta có: 3x - 6 = 0 ⇔ 3x = 6 ⇔ x = 2
→ Phương trình có tập nghiệm là S = {2}
Chọn đáp án B.
Bài 5: Phương trình - 1/2x = - 2 có nghiệm là?
A. x = - 2.
B. x = - 4.
C. x = 4.
D. x = 2.
Ta có: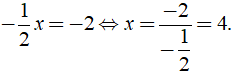
Vậy phương trình có tập nghiệm là x = 4.
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Tìm tập nghiệm của các phương trình sau đây?
a) - 3x = - 7/2
b) 2x = 6.
c) - 5/2x = - 5.
Hướng dẫn:
a) Ta có: - 3x = - 7/2 ⇔ x = (- 7/2)/ - 3 = 7/6.
Vậy tập nghiệm của phương trình là S = {7/6}
b) Ta có: 2x = 6 ⇔ x = 6/2 ⇔ x = 3.
Vậy phương trình có tập nghiệm là S = {3}
c) Ta có: - 5/2x = - 5 ⇔ x = - 5/(- 5/2) ⇔ x = 1/2.
Vậy tập nghiệm của phương trình là S = {1/2}
Bài 2: Chứng minh rằng các phương trình sau tương đương
a) 2x = 6 và 1,5x = 4,5.
b) - 2x = 4 và x/2 = - 1
Hướng dẫn:
a) Ta có:
+ Phương trình 2x = 6 ⇔ x = 3 có tập nghiệm là S = {3}
+ Phương trình 1,5x = 4,5 ⇔ x = 4,5/1,5 ⇔ x = 3 có tập nghiệm là S = {3}
→ Hai phương trình có cùng tập nghiệm.
→ Hai phương trình tương đương.
b) Ta có:
+ Phương trình - 2x = 4 ⇔ x = - 2 có tập nghiệm là S = {- 2}
+ Phương trình x/2 = - 1 ⇔ x = - 2 có tập nghiệm là S = {- 2}
→ Hai phương trình có cùng tập nghiệm.
→ Hai phương trình tương đương.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Mở đầu về phương trình. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








