Hình bình hành
Chuyên đề: Hình bình hành
Chuyên đề Toán học lớp 8: Hình bình hành tóm tắt lý thuyết kèm bài tập thực hành về hình bình hành, giúp các bạn học sinh học tốt môn Toán học lớp 8 hơn. Mời các bạn tham khảo.
A. Lý thuyết Hình bình hành
1. Định nghĩa hình bình hành
- Hình bình hành là tứ giác có các cạnh đối song song
- Tứ giác ABCD là hình bình hành ⇔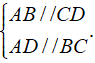

Chú ý đặc biệt: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)
2. Tính chất hình bình hành
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .
Hướng dẫn:
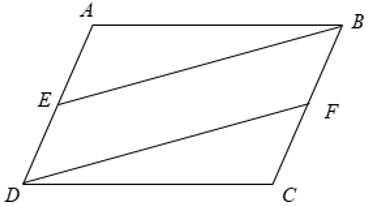
Xét tứ giác BEDF có 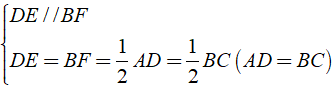
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ (1)
BEDF là hình bình hành nên BEDˆ = DFBˆ (2)
Mà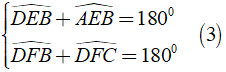
Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ (4)
Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 1800 (5)
Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)
B. Các dạng Toán thường gặp
Dạng 1: Vận dụng tính chất hình bình hành để chứng minh tính chất hình học và tính toán
Phương pháp: Sử dụng tính chất hình bình hành
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dạng 2: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành
Phương pháp: Dấu hiệu nhận biết:
+ Tứ giác có đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
C. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Chọn phương án sai trong các phương án sau?
A. Tứ giác có các cạnh đối song song là hình bình hành.
B. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
→ Đáp án C sai.
Chọn đáp án C.
Bài 2: Chọn phương án đúng trong các phương án sau.
A. Hình bình hành là tứ giác có hai cạnh đối song song.
B. Hình bình hành là tứ giác có các góc bằng nhau.
C. Hình bình hành là tứ giác có các cạnh đối song song.
D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
→ Đáp án C đúng.
Chọn đáp án C.
Bài 3: Cho hình bình hành ABCD có Aˆ = 1200, các góc còn lại của hình bình hành là?
A. Bˆ = 600, Cˆ = 1200, Dˆ = 600.
B. Bˆ = 1100, Cˆ = 800, Dˆ = 600.
C. Bˆ = 800, Cˆ = 1200, Dˆ = 800.
D. Bˆ = 1200, Cˆ = 600, Dˆ = 1200.

Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
⇒ Aˆ = Cˆ = 1200.
Khi đó ta có: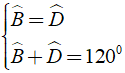 ⇒ Bˆ = Dˆ = 600
⇒ Bˆ = Dˆ = 600
Chọn đáp án A.
Bài 4: Cho hình bình hành ABCD có Aˆ - Bˆ = 200. Xác định số đo góc A và B?
A. Aˆ = 800, Bˆ = 1000
B. Aˆ = 1000, Bˆ = 800
C. Aˆ = 800, Bˆ = 600
D. Aˆ = 1200, Bˆ = 1000
Theo giả thiết, ta có: Aˆ - Bˆ = 200 ⇒ Aˆ = Bˆ + 200
Mặt khác ABCD là hình bình hành nên Aˆ + Bˆ = 1800
Khi đó: 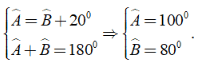
Chọn đáp án B.
Bài 5: Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
A. AC = BD
B. ΔABD cân tại A.
C. BI là đường trung tuyến của Δ ABC
D. Aˆ + Cˆ = Bˆ + Dˆ.
Trong hình bình hành các góc đối bằng nhau
Hay 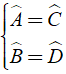 ⇒ Aˆ + Bˆ = Cˆ + Dˆ → đáp án D sai.
⇒ Aˆ + Bˆ = Cˆ + Dˆ → đáp án D sai.
+ ΔABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A, C xuống BD.
a) Chứng minh AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Hướng dẫn:
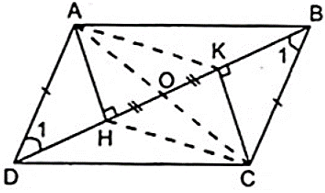
a) Từ giả thiết ta có: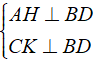 ⇒ AH // CK (1)
⇒ AH // CK (1)
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
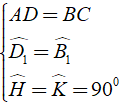 ⇒ ΔADH = ΔCBK (trường hợp cạnh huyền – góc nhọn)
⇒ ΔADH = ΔCBK (trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tương ứng bằng nhau) (2)
Từ (1) và (2) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Bài 2: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK // CI
b) DM = MN = NB
Hướng dẫn:
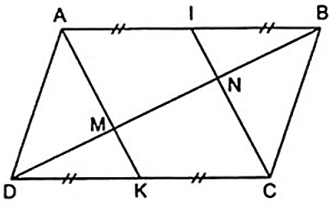
a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
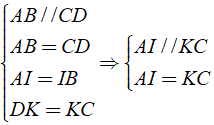
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
b) Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: ![]()
Mặt khác, ta lại có: AI = IB, CK = KD theo giả thiết:
Áp dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
![]() ⇒ DM = MN = NB
⇒ DM = MN = NB
D. Bài tập tự luyện
Bài 1. Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.
a) Chứng minh DE // BF;
b) Tứ giác DEBF là hình gì?
Bài 2. Cho tam giác ABC. Từ một điểm E trên cạnh AC vẽ đường thẳng song song với BC cắt AB tại F và đường thẳng song song với AB cắt BC tại D. Giả sử AE = BF, chứng minh:
a) Tam giác AED cân
b) AD là phân giác của góc A.
Bài 3. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và I, K là trung điểm của các đường chéo AC, BD. Chứng minh:
a) Các tứ giác MNPQ, INKQ là hình bình hành.
b) Các đường thẳng MP, NQ, IK đồng quy.
Bài 4. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh tứ giác MNPQ là hình bình hành;
b) So sánh chu vi tứ giác MNPQ và tổng hai đường chéo của tứ giác ABCD.
Bài 5. Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của BC, CD. Hai đường thẳng AM, AN cắt BD tại E, F. CMR:
a) E, F lần lượt là trọng tâm của các tam giác ABC và ACD;
b) EB = EF = DF.
Bài 6. Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Gọi M, N, P, Q lần lượt là trung điểm của AF, EC, DE, BF. Chứng minh các tứ giác EQFM, ENFP, MNPQ là hình bình hành.
Bài 7. Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC, O là trung điểm của MN. Gọi I là điểm đối xứng của A qua O. Chứng minh:
a) Tứ giác AMIN là hình bình hành.
b) Tứ giác MNIB là hình bình hành.
c) Tứ giác MNCI là hình bình hành.
d) B và C đối xứng nhau qua I.
Bài 8. Cho tam giác ABC và O là điểm nằm trong tam giác, M, N theo thứ tự là trung điểm của BC, CA. Gọi A’, B’ lần lượt là các điểm đối xứng của điểm O qua M, N. Chứng minh:
a) Tứ giác AB’CO là hình bình hành.
b) Tứ giác BOCA’ là hình bình hành.
c) Tứ giác AB’A’B là hình bình hành.
Bài 9. Cho tam giác ABC cân tại A. Gọi M, N, P lần lượt là trung điểm của BC, AC, AB. Điểm E đối xứng với P qua N, điểm F đối xứng với N qua đường thẳng BC.
a) Tứ giác ANFM là hình gì? Vì sao?
b) Đường thẳng ME cắt đường thẳng AB tại K. Chứng minh K đối xứng với P qua B.
c) Chứng minh ba điểm C, E, F thẳng hàng.
Bài 10. Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C.
a) Chứng minh AEBC và ABFC là các hình bình hành.
b) Các điểm E và F có đối xứng với nhau qua điểm B không? Vì sao?
c) Tìm điều kiện của hình bình hành ABCD để E đối xứng với F qua đường thẳng BD.
Bài 11. Cho tam giác ABC cân tại A. Trên AB lấy D, trên AC lấy E sao cho AD = CE. Gọi O là trung điểm của DE, K là giao điểm của AO và BC. Tứ giác ADKE là hình bình hành.
Bài 12. Cho tứ giác ABCD có M, N lần lượt là trung điểm của AB, CD. Lấy P, Q lần lượt thuộc cạnh BC, AD (PB ≠ PC, QA ≠ QD). Biết tứ giác MPNQ là hình bình hành. Chứng minh BC // AD.
Bài 13. Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh:
a) EMFN là hình bình hành;
b) Các đường thẳng AC, BD, EF, GH đồng quy.
Bài 14*. Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA’, BB’, CC’, DD’ là các đường vuông góc kẻ từ A, B. C, D đến đường thẳng xy. Chứng minh AA’ = BB’ + DD'.
Bài 15*. Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’, BB’, CC’, DD’ là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA’, BB’, CC’, DD'.









