Đa giác - Đa giác đều
Chuyên đề Toán học lớp 8: Đa giác - Đa giác đều được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Đa giác - Đa giác đều
A. Lý thuyết
1. Khái niệm về đa giác
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Chú ý: Từ nay nếu nhắc đến đa giác thì ta quy ước đó là đa giác lồi
2. Đa giác đều
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
3. Mở rộng
a) Góc trong đa giác
+ Tổng số đo các góc của đa giác n cạnh là (n - 2).1800.
+ Số đo của một góc của đa giác đều n cạnh là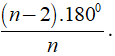
b) Số đường chéo của đa giác n cạnh
Số đường chéo của đa giác n cạnh là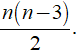
Ví dụ: Cho một đa giác đều có 20 cạnh. Tính số đo một góc và số đường chéo của đa giác đều đó?
Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là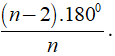
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
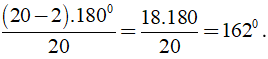
+ Số đường chéo của đa giác n cạnh là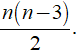
Khi đó số đường chéo của đa giác đều 20 cạnh là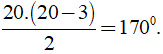
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là (n - 2).1800.
Khi đó tổng các góc của đa giác lồi 8 cạnh là (8 - 2).1800 = 10800.
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là ((n - 2).1800)/n.
Khi đó số đo của hình bát giác đều là ((8 - 2).1800)/8 = 1350.
⇒ Đáp án D sai.
Bài 2: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là?
A. 12. B. 13. C. 14. D. Kết quả khác.
Số đường chéo của đa giác n cạnh là (n(n - 3))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7(7 - 3))/2 = 14 (đường chéo)
Chọn đáp án C.
Bài 3: Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5. B. 6. C. 4. D. 7.
Số đường chéo của đa giác n cạnh là (n(n - 3))/2. (n ∈ N, n ≥ 3)
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n2 - 3n - 2n = 0
⇔ n2 - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔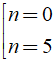 
So sánh điều kiện ta có n = 5 thỏa mãn.
II. Bài tập tự luận
Bài 1: Cho đa giác đều có 14 cạnh. Tính :
a) Tổng số đo góc của đa giác đó
b) Số đo một góc của đa giác
c) Số đường chéo của đa giác.
Hướng dẫn:
a) Tổng số đo các góc của đa giác n cạnh là (n - 2).1800.
Tổng số đo của đa giác 14 cạnh là (14 - 2).1800 = 21600.
b) Số đo của một góc của đa giác đều n cạnh là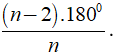
Số đo một góc của đa giác 14 cạnh là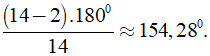
c) Số đường chéo của đa giác n cạnh là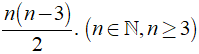
Số đường chéo của đa giác 14 cạnh là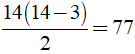
đường chéo
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Đa giác - Đa giác đều. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
