Phân tích đa thức thành nhân tử
Chuyên đề Toán học lớp 8: Phân tích đa thức thành nhân tử được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Phân tích đa thức thành nhân tử
A. Lý thuyết
I. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG
1. Khái niệm về phương pháp đặt nhân tử chung
Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
Ứng dụng: Việc phân tích đa thức thành nhân tử giúp ta có thể thu gọc biểu thức, tính nhanh và giải phương trình dễ dàng.
2. Phương pháp đặt nhân tử chung
+ Khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.
+ Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.
Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.
3. Ví dụ áp dụng
Ví dụ: Phân tích đa thức sau thành nhân tử
a, 4x2 - 6x
b, 9x4y3 + 3x2y4
Hướng dẫn:
a) Ta có : 4x2 - 6x = 2x.2x - 3.2x = 2x(2x - 3).
b) Ta có: 9x4y3 + 3x2y4 = 3x2y3.3x + 3x2y3 = 3x2y3(3x + 1)
II. PHÂN THÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP DÙNG HẰNG ĐẲNG THỨC
1. Phương pháp dùng hằng đẳng thức
+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.
+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.
2. Ví dụ áp dụng
Ví dụ: Phân tích đa thức sau thành nhân tử
a, 9x2 - 1
b, x2 + 6x + 9.
Hướng dẫn:
a) Ta có: 9x2 - 1 = (3x )2 - 12 = (3x - 1)(3x + 1)
(áp dụng hằng đẳng thức A2 - B2 = (A - B)(A + B)
b) Ta có: x2 + 6x + 9 = x2 + 2.x.3 + 32 = (x + 3)2.
(áp dụng hằng đẳng thức (A + B)2 = A2 + 2AB + B2
III. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP NHÓM HẠNG TỬ
1. Phương pháp nhóm hạng tử
+ Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.
+ Ta nhận xét để tìm cách nhóm hạng tử một cách thích hợp (có thể giao hoán và kết hợp các hạng tử để nhóm) sao cho sau khi nhóm, từng nhóm đa thức có thế phân tích được thành nhân tử bằng phương pháp đặt nhân tử chung, bằng phương pháp dùng hằng đẳng thức. Khi đó đa thức mới phải xuất hiện nhân tử chung.
+ Ta áp dụng phương pháp đặt thành nhân tử chung để phân tích đa thức đã cho thành nhân tử.
2. Chú ý
+ Với một đa thức, có thể có nhiều cách nhóm các hạng tử một cách thích hợp.
+ Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (không còn phân tích được nữa).
+ Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.
+ Khi nhóm các hạng tử, phải chú ý đến dấu của đa thức.
3. Ví dụ áp dụng
Ví dụ: Phân tích các đa thức sau thành nhân tử.
a, x2 - 2xy + xy2 - 2y3.
b, x2 + 4x - y2 + 4.
Hướng dẫn:
a) Ta có x2 - 2xy + xy2 - 2y3 = (x2 - 2xy) + (xy2 - 2y3) = x(x - 2y) + y2(x - 2y)
= (x + y2)( x - 2y)
b) Ta có x2 + 4x - y2 + 4 = (x2 + 4x + 4) - y2 = (x + 2)2 - y2 = (x + 2 - y)(x + y + 2)
IV. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ BẰNG PHỐI HỢP NHIỀU PHƯƠNG PHÁP
1. Phương pháp thực hiện
Ta tìm hướng giải bằng cách đọc kỹ đề bài và rút ra nhận xét để vận dụng các phương pháp đã biết:
+ Đặt nhân tử chung
+ Dùng hằng đẳng thức
+ Nhóm nhiều hạng tử và phối hợp chúng
⇒ Để phân tích đa thức thành nhân tử.
2. Chú ý
Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.
3. Ví dụ áp dụng
Ví dụ: Phân tích đa thức thành nhân tử
x2 + 4x - 2xy - 4y + y2.
2xy - x2 - y2 + 16.
Hướng dẫn:
a) Ta có x2 + 4x - 2xy - 4y + y2 = (x2 - 2xy + y2) + (4x - 4y) = (x - y)2 + 4(x - y)
= (x - y)(x - y + 4).
b) Ta có: 2xy - x2 - y2 + 16 = 16 - (x2 - 2xy + y2) = 16 - (x - y)2
= (4 - x + y)(4 + x - y).
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Đa thức 4x(2y - z) + 7y(z - 2y) được phân tích thành nhân tử là?
A. (2y + z) 4x + 7y)
B. (2y - z )(4x - 7y)
C. (2y + z )(4x - 7y)
D. (2y - z )(4x + 7y)
Ta có 4x(2y - z) + 7y(z - 2y) = 4x(2y - z) - 7y(2y - z) = (2y - z)(4x - 7y).
Chọn đáp án B.
Bài 2: Đa thức x3(x2 - 1 ) - (x2 - 1) được phân tích thành nhân tử là?
A. (x - 1)2(x + 1)(x2 + x + 1)
B. (x3 - 1)(x2 - 1)
C. (x - 1)( x + 1)(x2 + x + 1)
D. (x - 1)2( x + 1)(x2 + x + 1)
Ta có x3(x2 - 1) - (x2 - 1) = (x2 - 1)(x3 - 1) = (x - 1)(x + 1)(x - 1)(x2 + x + 1)
= (x - 1)2(x + 1 (x2 + x + 1)
Chọn đáp án D.
Sai lầm: Nhiều em học sinh mắc phải sai lầm là nhóm nhân tử (x2 - 1)(x3 - 1) mà không nhận ra trong hai đa thức (x2 - 1) và (x3 - 1) có nhân tử chung là (x - 1) để đặt làm nhân tử chung. Dẫn đến nhiều em sẽ chọn đáp án B.
Bài 3: Tìm giá trị y thỏa mãn 49(y - 4)2 - 9(y + 2)2 = 0 ?
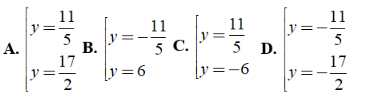
Ta có 49(y - 4)2 - 9(y + 2)2 = 0
⇔ 49( y2 - 8y + 16 ) - 9(y2 + 4y + 4) = 0
⇔ 49y2 - 392y + 784 - 9y2 - 36y - 36 = 0
⇔ 40y2 - 428y + 748 = 0 ⇔ 4(10y2 - 107y + 187) = 0
⇔ 4[(10y2 - 22y) - (85y - 187)] = 0 ⇔ 4[2y(5y - 11) - 17(5y - 11) ] = 0
⇔ 4(5y - 11)(2y - 17) = 0
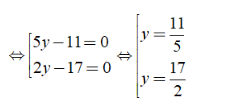
Chọn đáp án A.
Bài 4: Tính giá trị của biểu thức A = x2 - y2 + 2y - 1 với x=3 và y=1.
A. A = - 9. B. A = 0. C. A = 9. D. A = - 1.
Ta có A = x2 - y2 + 2y - 1 = x2 - (y2 - 2y + 1)
= x2 - (y - 1)2 = (x - y + 1)(x + y - 1) (hằng đẳng thức a2 - b2 = (a - b)(a + b).
Khi đó với x = 3 và y = 1, ta có A = (3 - 1 + 1)(3 + 1 - 1) = 3.3 = 9.
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Phân tích các đa thức sau thành nhân tử
a, (ab - 1)2 + (a + b)2
b, x3 + 2x2 + 2x + 1
c, x2 - 2x - 4y2 - 4y
Hướng dẫn:
a) Ta có (ab - 1)2 + (a + b)2 = a2b2 - 2ab + 1 + a2 + 2ab + b2
= a2b2 + a2 + b2 + 1 = (a2b2 + a2) + (b2 + 1)
= a2(b2 + 1) + (b2 + 1) = (a2 + 1)(b2 + 1)
b) Ta có x3 + 2x2 + 2x + 1 = (x3 + 1) + (2x2 + 2x)
= (x + 1)(x2 - x + 1) + 2x(x + 1) = (x + 1)(x2 + x + 1)
c) Ta có x2 - 2x - 4y2 - 4y = (x2 - 4y2) - (2x + 4y)
= (x - 2y)(x + 2y) - 2(x + 2y)
= (x + 2y)(x - 2y - 2).
Bài 2: Tính giá trị của biểu thức sau A = x6 - 2x4 + x3 + x2 - x, biết x3 - x = 6.
Hướng dẫn:
Ta có: A = x6 - 2x4 + x3 + x2 - x = (x6 - 2x4 + x2) + (x3 - x)
= (x3 - x)2 + (x3 - x)
Với x3 - x = 6 = (x3 - x)2 + (x3 - x), ta có A = 62 - 6 = 36 - 6 = 30.
Vậy A = 30.
Bài 3: Tìm x biết
a) x2 - 5x + 6 + (x - 1)(x + 2) = 0
b) x3 + x2 - 2 = 0
Hướng dẫn:
a) Ta có: x2 - 5x + 6 + (x - 1)(x - 2) = 0
⇔ [(x2 - 2x) - (3x - 6)] + (x - 1)(x - 2) = 0
⇔ (x - 2)(x - 3) + (x - 1)(x - 2) = 0
⇔ (x - 2)(2x - 4) = 0
⇔ 2( x - 2 )2 = 0 ⇔ x = 2
Vậy giá trị x cần tìm là x = 2.
b) Ta có: x3 + x2 - 2 = 0
⇔ (x3 - 1) + (x2 - 1) = 0
⇔ (x - 1)(x2 + x + 1) + (x - 1 (x + 1) = 0
⇔ (x - 1)(x2 + x + 1 + x + 1) = 0
⇔ (x - 1)[(x + 1)2 + 1] = 0 ⇔ x = 1 (vì ( x + 1)2 + 1 ≥ 1 ∀ x)
Vậy giá trị x cần tìm là x = 1.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Phân tích đa thức thành nhân tử. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








