Phương trình chứa ẩn ở mẫu
Chuyên đề: Phương trình chứa ẩn ở mẫu
Chuyên đề Toán học lớp 8: Phương trình chứa ẩn ở mẫu được VnDoc sưu tầm và đăng tải tổng hợp lý thuyết cùng với bài tập phương trình chứa ẩn ở mẫu giúp các em củng cố kiến thức và nâng cao kỹ năng giải bài. Mời các em cùng tham khảo nhé.
Để ôn tập hiệu quả dạng bài tập này, mời các bạn tham khảo thêm:
Bài tập Toán lớp 8: Phương trình chứa ẩn ở mẫu
A. Lý thuyết Phương trình chứa ẩn ở mẫu
1. Tìm điều kiện xác định của một phương trình
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0.
Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
Ví dụ: Tìm điều kiện xác định của các phương trình sau
a) (x - 1)/(x + 2) + 1 = 1/(x - 2).
b) (x - 1)/(1 - 2x) = 1.
Hướng dẫn:
a) Ta thấy x + 2 ≠ 0 khi x ≠ - 2 và x - 2 ≠ 0 khi x ≠ 2.
Do đó ĐKXĐ của phương trình (x - 1)/(x + 2) + 1 = 1/(x - 2) là x ≠ ± 2.
b) Ta thấy 1 - 2x ≠ 0 khi x ≠ 1/2.
Do đó ĐKXĐ của phương trình (x - 1)/(1 - 2x) = 1 là x ≠ 1/2.
2. Giải phương trình chứa ẩn ở mẫu
Ta thường qua các bước:
Bước 1: Tìm điều kiện xác của phương trình
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
Bước 3: Giải phương trình tìm được.
Bước 4: Kết luận.
Nghiệm của phương trình là giá trị của ẩn thoả mãn ĐKXĐ của phương trình.
Ví dụ 1: Giải phương trình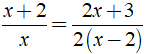
Hướng dẫn:
Bước 1: Điều kiện xác định: x ≠ 0; x ≠ 2.
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu
Ta có:
⇒ 2(x - 2)(x + 2) = x(2x + 3)
Bước 3: Giải phương trình
Ta có: 2(x - 2)(x + 2) = x(2x + 3) ⇔ 2(x2 - 4) = 2x2 + 3x
⇔ 2x2 - 8 = 2x2 + 3x ⇔ 3x = - 8 ⇔ x = - 8/3.
Bước 4: Kết luận
So sánh với ĐKXĐ, ta thấy x = - 8/3 thỏa mãn.
Vậy phương trình đã cho có tập nghiệm S = { - 8/3 }.
Ví dụ 2: Giải phương trình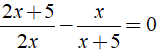
Hướng dẫn:
+ ĐKXĐ: x ≠ 0; x ≠ - 5.
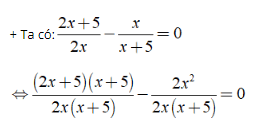
⇒ (2x + 5)(x + 5) - 2x2 = 0
⇔ 2x2 + 10x + 5x + 25 - 2x2 = 0 ⇔ 15x = - 25 ⇔ x = - 5/3.
+ So sánh với ĐKXĐ ta thấy x = - 5/3 thỏa mãn điều kiện.
Vậy phương trình đã cho có tập nghiệm là S = {- 5/3}.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình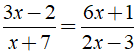 là?
là?
A. x = - 1.
B. x = - 1/56.
C. x = 1.
D. x = 1/56.
+ ĐKXĐ: x ≠ - 7;x ≠ 3/2.
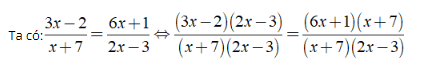
⇔ (3x - 2)(2x - 3) = (6x + 1)(x + 7)
⇔ 6x2 - 13x + 6 = 6x2 + 43x + 7
⇔ 56x = - 1 ⇔ x = - 1/56.
Vậy phương trình đã cho có nghiệm x = - 1/56.
Chọn đáp án B.
Bài 2: Nghiệm của phương trình (x + 1)/(3 - x) = 2 là?
A. x = - 5/3.
B. x = 0.
C. x = 5/3.
D. x = 3.
+ ĐKXĐ: x ≠ 3.
+ Ta có: (x + 1)/(3 - x) = 2 ⇔ x + 1 = 2( 3 - x )
⇔ x + 1 = 6 - 2x ⇔ 3x = 5 ⇔ x = 5/3.
Vậy phương trình có nghiệm là x = 5/3.
Chọn đáp án C.
Bài 3: Tập nghiệm của phương trình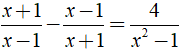 là?
là?
A. S = {± 1}.
B. S = {0;1}.
C. S = {1}.
D. S = {Ø}.
+ ĐKXĐ: x2 - 1 ≠ 0 ⇒ x ≠ ± 1.
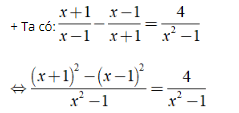
⇔ (x + 1)2 - (x - 1)2 = 4
⇔ x2 + 2x + 1 - x2 + 2x - 1 = 4
⇔ 4x = 4 ⇔ x = 1.
So sánh điều kiện, ta thấy x = 1 không thỏa mãn.
Vậy phương trình đã cho có tập nghiệm là S = { Ø }.
Chọn đáp án D.
Bài 4: Nghiệm của phương trình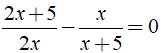 là?
là?
A. x = 5/3.
B. x = - 5/3.
C. x = - 2.
D. x = 2.
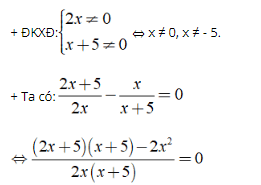
⇔ (2x2 + 15x + 25) - 2x2 = 0
⇔ 15x + 25 = 0 ⇔ x = - 5/3.
Vậy phương trình đã cho có nghiệm là x = - 5/3.
Chọn đáp án B.
Bài 5: Giá trị của m để phương trình (x - m)/(x + 2) = 2 có nghiệm x = - 3 là?
A. m = 0.
B. m = 1.
C. m = - 1.
D. m = 2.
+ Điều kiện: x ≠ - 2.
+ Phương trình có nghiệm x = - 3, khi đó ta có: (- 3 - m)/(- 3 + 2) = 2 ⇔ (- m - 3)/(- 1) = 2
⇔ m + 3 = 2 ⇔ m = - 1.
Vậy m = - 1 là giá trị cần tìm.
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Giải các phương trình sau:
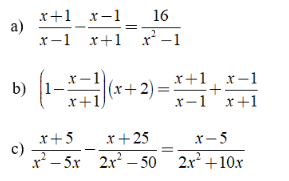
Hướng dẫn:
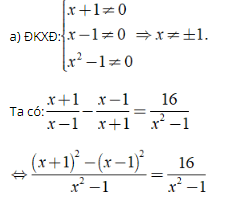
⇔ (x + 1)2 - (x - 1)2 = 16
⇔ (x2 + 2x + 1) - (x2 - 2x + 1) = 16
⇔ 4x = 16 ⇔ x = 4.
Vây phương trình đã cho có nghiệm x = 4.
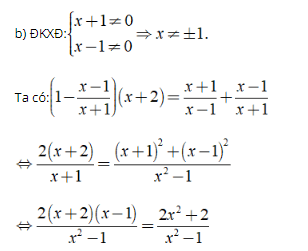
⇔ 2(x2 + x - 2) = 2x2 + 2
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.

⇔ 2(x2 + 10x + 25) - (x2 + 25x) = x2 - 10x + 25
⇔ x2 - 5x + 50 = x2 - 10x + 25
⇔ 5x = - 25 ⇔ x = - 5.
Vậy phương trình đã cho có nghiệm x = - 5.
Bài 2: Giải các phương trình sau:
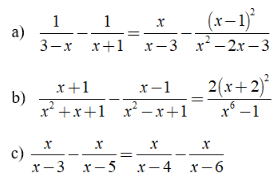
Hướng dẫn:
a) ĐKXĐ: x ≠ - 1;x ≠ 3.
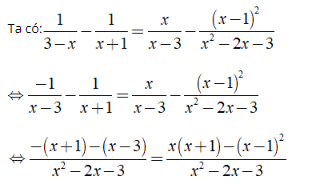
⇔ - x - 1 - x + 3 = x2 + x - x2 + 2x - 1
⇔ 5x = 3 ⇔ x = 3/5.
Vậy phương trình đã cho có nghiệm là x = 3/5.
b) ĐKXĐ: x ≠ 3, x ≠ 4, x ≠ 5, x ≠ 6.
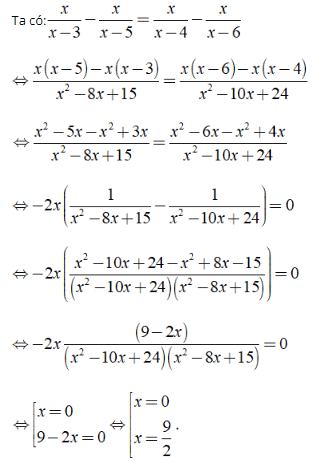
Vậy phương trình đã cho có nghiệm là x = 0;x = 9/2.
c) ĐKXĐ: x ≠ 1.
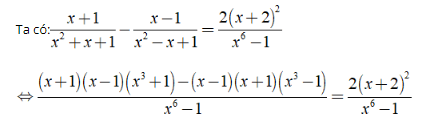
⇔ (x2 - 1 )( x3 + 1) - (x2 - 1)(x3 - 1) = 2(x2 + 4x + 4)
⇔ (x5 + x2 - x3 - 1) - (x5 - x2 - x3 + 1) = 2(x2 + 4x + 4)
⇔ 2x2 - 2 = 2x2 + 8x + 8
⇔ 8x = - 10 ⇔ x = - 5/4.
Vậy phương trình đã cho có nghiệm là x = - 5/4.
Bài 3. Cho hai biểu thức: ![]() . Tìm x sao cho A = B.
. Tìm x sao cho A = B.
Lời giải
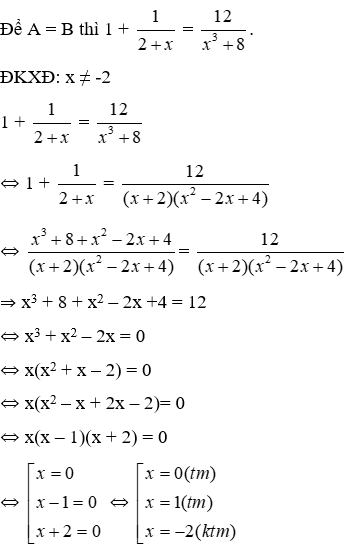
Vậy để A = B thì x = 0 hoặc x = 1
...................................
Phương trình chứa ẩn ở mẫu được VnDoc chia sẻ trên đây. Với tài liệu này ngoài giúp các em nắm chắc kiến thức cơ bản còn giúp các em nâng cao kỹ năng giải bài tập, nhất là các bài tập về phương trình mẫu ở ẩn. Chúc các em học tốt, ngoài ra để nâng cao kỹ năng giải toán các em tham khảo thêm bài Tổng hợp kiến thức Toán lớp 8 hoặc Bài tập toán nâng cao lớp 8 này nhé.
Ngoài Phương trình chứa ẩn ở mẫu, các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 8, học kì 2 lớp 8 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt
| Đặt câu hỏi về học tập, giáo dục, giải bài tập của bạn tại chuyên mục Hỏi đáp của VnDoc | |
| Hỏi - Đáp | Truy cập ngay: Hỏi - Đáp học tập |








