Giải bài tập SBT Toán 8 bài 5: Phương trình chứa ẩn ở mẫu

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 5: Phương trình chứa ẩn ở mẫu được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 3: Phương trình đưa về dạng ax + b = 0

Giải bài tập SBT Toán 8 bài 4: Phương trình tích

Giải bài tập SBT Toán 8 bài 6-7: Giải bài toán bằng cách lập phương trình

Câu 1: Em hãy chọn khẳng định đúng trong hai khẳng định sau đây:

1. Hai phương trình tương đương với nhau thì phải có cùng điều kiện xác định.
2. Hai phương trình có cùng điều kiện xác định có thể không tương đương với nhau.

Lời giải:

Phát biểu trong câu b là đúng.

Câu 2: Giải các phương trình sau:

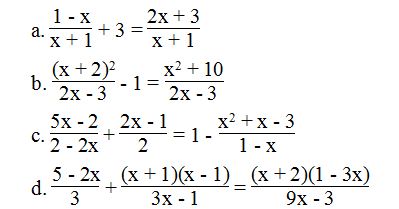
Lời giải:

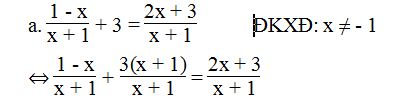
⇔ 1 – x + 3(x + 1) = 2x + 3

⇔ 1 – x + 3x + 3 – 2x – 3 = 0

⇔ 0x = - 1

Phương trình vô nghiệm.

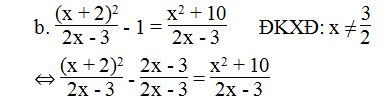
⇔ (x + 2)² – (2x – 3) = x2 + 10

x² + 4x + 4 – 2x + 3 – x2 – 10 = 0

⇔ 2x = 3 ⇔ x = 3/2 (loại)

Phương trình vô nghiệm.

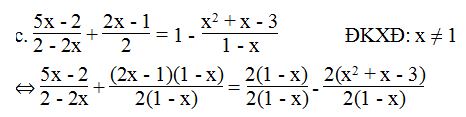
⇔ 5x – 2 + (2x – 1)(1 – x) = 2(1 – x) – 2(x² + x – 3)

⇔ 5x – 2 + 2x – 2x² – 1 + x – 2 + 2x + 2x² + 2x – 6 = 0

⇔ 5x + 2x + x + 2x + 2x = 2 + 6 + 2 + 1 ⇔ 12x = 11

⇔ x = 11/12 (thoả)

Vậy phương trình có nghiệm x = 11/12

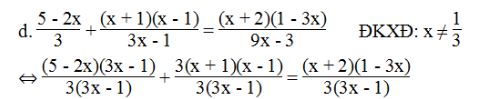
⇔ (5 – 2x)(3x – 1) + 3(x + 1)(x – 1) = (x + 2)(1 – 3x)

⇔ 15x – 5 – 6x2 + 2x + 3x² – 3 = x – 3x² + 2 – 6x

⇔ - 6x² + 3x² + 3x² + 15x + 2x – x + 6x = 2 + 5 + 3

⇔ 22x = 10 ⇔ x = 5/11 (thỏa)

Vậy phương trình có nghiệm x = 5/11.

Câu 3: Giải các phương trình sau:

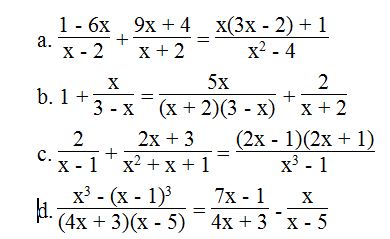
Lời giải:

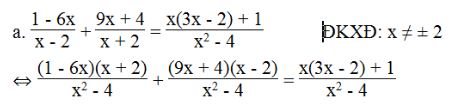
⇔ (1 – 6x)(x + 2) + (9x + 4)(x – 2) = x(3x – 2) + 1

⇔ x + 2 – 6x² – 12x + 9x2 – 18x + 4x – 8 = 3x² – 2x + 1

⇔ - 6x² + 9x² – 3x2 + x – 12x – 18x + 4x + 2x = 1 – 2 + 8

⇔ - 23x = 7 ⇔ x = - 7/23 (thỏa)

Vậy phương trình có nghiệm x = - 7/23

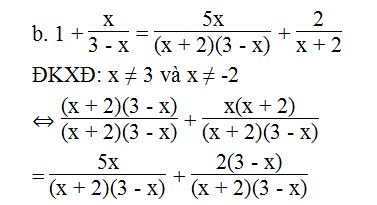
⇔ (x + 2)(3 – x) + x(x + 2) = 5x + 2(3 – x)

⇔ 3x – x² + 6 – 2x + x² + 2x = 5x + 6 – 2x

⇔ x² – x² + 3x – 2x + 2x – 5x + 2x = 6 – 6 ⇔ 0x = 0

Phương trình đã cho có nghiệm đúng với mọi giá trị của x thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x ∈ R / x ≠ 3 và x ≠ -2

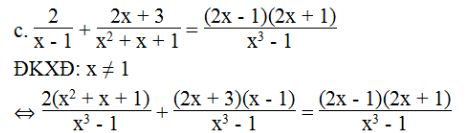
⇔ 2(x² + x + 1) + (2x + 3)(x – 1) = (2x – 1)(2x + 1)

⇔ 2x² + 2x + 2 + 2x² – 2x + 3x – 3 = 4x² – 1

⇔ 2x² + 2x² – 4x² + 2x – 2x + 3x = -1 – 2 + 3

⇔ 3x = 0 ⇔ x = 0 (thỏa)

Vậy phương trình có nghiệm x = 0.

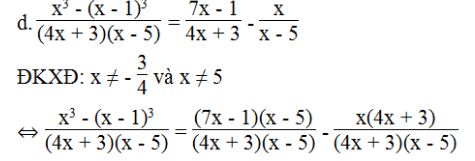
⇔ x³ – (x – 1)³ = (7x – 1)(x – 5) – x(4x + 3)

⇔ x³ – x³ + 3x² – 3x + 1 = 7x² – 35x – x + 5 – 4x² – 3x

⇔ 3x² – 7x² + 4x² – 3x + 35x + x + 3x = 5 – 1

⇔ 36x = 4 ⇔ x = 1/9 (thoả)

Vậy phương trình có nghiệm x = 1/9

Câu 4: Giải các phương trình sau:

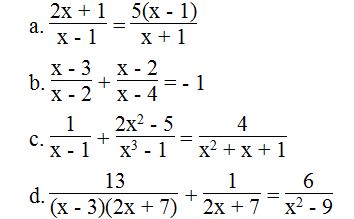
Lời giải:

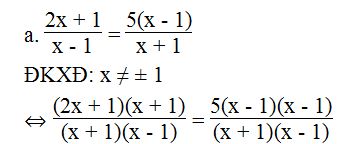
⇔ (2x + 1)(x + 1) = 5(x – 1)(x – 1)

⇔ 2x² + 2x + x + 1 = 5x² – 10x + 5

⇔ 2x² – 5x² + 2x + x + 10x + 1 – 5 = 0

⇔ - 3x² + 13x – 4 = 0 ⇔ 3x² – x – 12x + 4 = 0

⇔ x(3x – 1) – 4(3x – 1) = 0 ⇔ (x – 4)(3x – 1) = 0

⇔ x – 4 = 0 hoặc 3x – 1 = 0

x – 4 = 0 ⇔ x = 4 (thỏa)

3x – 1 = 0 ⇔ x = 1/3 (thỏa)

Vậy phương trình có nghiệm x = 4 hoặc x = 1/3

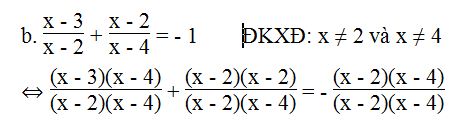
⇔ (x – 3)(x – 4) + (x – 2)(x – 2) = - (x – 2)(x – 4)

⇔ x² – 4x – 3x + 12 + x² – 2x – 2x + 4 = - x² + 4x + 2x – 8

⇔ 3x(x – 3) – 8(x – 3) = 0 ⇔ (3x – 8)(x – 3) = 0

⇔ 3x – 8 = 0 hoặc x – 3 = 0

3x – 8 = 0 ⇔ x = 8/3 (thỏa)

x – 3 = 0 ⇔ x = 3 (thỏa)

Vậy phương trình có nghiệm x = 8/3 hoặc x = 3

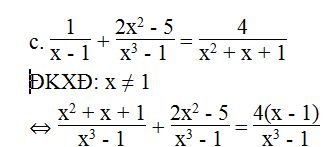
⇔ x² + x + 1 + 2x² – 5 = 4(x – 1)

⇔ x² + x + 1 + 2x² – 5 = 4x – 4 ⇔ 3x² – 3x = 0 ⇔ 3x(x – 1) = 0

⇔ x = 0 (thỏa) hoặc x – 1 = 0 ⇔ x = 1 (loại)

Vậy phương trình có nghiệm x = 0

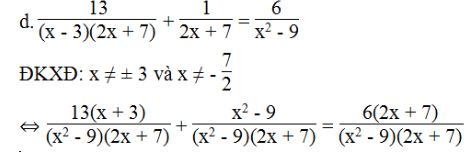
⇔ 13(x + 3) + x² – 9 = 6(2x + 7)

⇔ 13x + 39 + x² – 9 = 12x + 42

⇔ x² + x – 12 = 0

⇔ x² – 3x + 4x – 12 = 0

⇔ x(x – 3) + 4(x – 3) = 0

⇔ (x + 4)(x – 3) = 0

⇔ x + 4 = 0 hoặc x – 3 = 0

x + 4 = 0 ⇔ x = -4 (thỏa)

x – 3 = 0 ⇔ x = 3 (loại)

Vậy phương trình có nghiệm x = -4.