Giải bài tập SBT Toán 8 bài 2: Định lí đảo và hệ quả của định lí Ta-lét
Bài tập môn Toán lớp 8
Giải bài tập SBT Toán 8 bài 2: Định lí đảo và hệ quả của định lí Ta-lét được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Giải bài tập SBT Toán 8 bài: Ôn tập chương II
Giải bài tập SBT Toán 8 bài 1: Định lí Ta-lét trong tam giác
Giải bài tập SBT Toán 8 bài 3: Tính chất đường phân giác của tam giác
Câu 1: Cho tam giác ABC có Cạnh BC = a, Trên cạnh AB lấy các điểm D và E sao cho AD = DE = Eb, Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M và N. Tính theo a độ dài các đoạn thẳng DM và EN.
Lời giải:
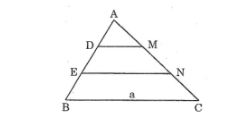
Ta có: AD = DE = EB = 13 AB (gt) (1)
Suy ra: AE = AD + DE = 23 AB (2)
Trong ΔABC, ta có: DM // BC (gt)
Câu 2: Cho hình vẽ bên
Cho biết MN // BC, AB =25cm, BC = 45cm, AM = 16cm, AN =10cm
Tính độ dài x, y của các đoạn thẳng MN,AC.
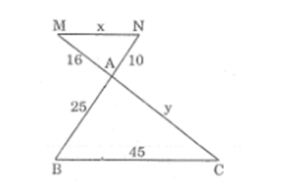
Lời giải:
Trong ΔABC,ta có: MN // BC (gt)
Suy ra: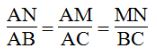
(Hệ quả định lí Ta-lét)
Suy ra: 10/25 = 16/y = x/45
Vậy: y = (25.16)/10 = 40
x = (10.45)/25 =18
Câu 3: Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB =24cm, AM=24cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.
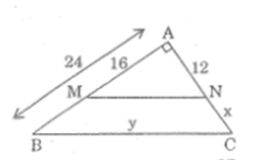
Lời giải:
Câu 4: Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O
Chứng minh rằng: Oa,OD = Ob,OC
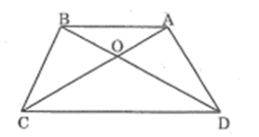
Lời giải:
Trong ΔOCD, ta có: AB // CD (gt)
Suy ra OA/OD = OB/OC (hệ quả định lí ta-lét)
Vậy Oa,OD = Ob,OC
Câu 5: Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm
a, Tính độ dài đoạn thẳng MN và đáy nhỏ Ab,
b,So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB
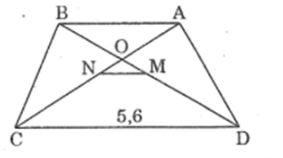
Lời giải:
a, Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: ΔADC = ΔBCD (c.c.c)
Suy ra : ∠(ACD) =∠( BDC)
Hay ∠(OCD) = ∠( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Trong ΔOAB, ta có: MN // AB
