Giải Toán 8 bài 5: Trường hợp đồng dạng thứ nhất
Giải bài tập Toán lớp 8 bài 5: Trường hợp đồng dạng thứ nhất
Giải Toán 8 bài 5: Trường hợp đồng dạng thứ nhất với các hướng dẫn giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 8. Lời giải Toán 8 gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo.
- Giải bài tập SGK Toán lớp 8 bài 1: Định lí Ta-lét trong tam giác
- Giải bài tập SGK Toán lớp 8 bài 2: Định lí đảo và hệ quả của định lí Ta-lét
- Giải bài tập SGK Toán lớp 8 bài 3: Tính chất đường phân giác của tam giác
Trả lời câu hỏi Toán 8 Tập 2 Bài 5 trang 73:
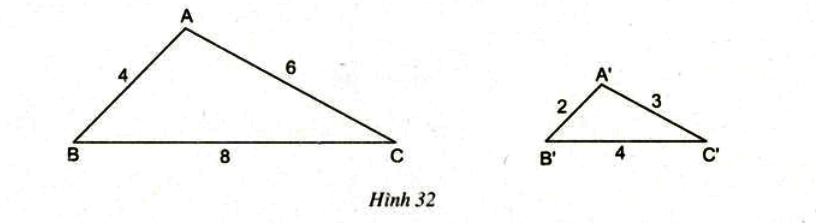
Hai tam giác ABC và A’B’C’ có kích thước như trong hình 32 (có cùng đơn vị đo là xentimet)
Trên các cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho
AM = A’B’ = 2cm; AN = A’C’ = 3cm.
Tính độ dài đoạn thẳng MN.
Có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN, A’B’C’?
Hướng dẫn giải:
Ta có: 
\(\begin{array}{l}\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}\\ \Rightarrow MN//BC\end{array}\) (theo định lý Talet đảo)
\(\begin{array}{l} \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{{MN}}{{BC}} = \dfrac{1}{2}\\ \Rightarrow MN = \dfrac{1}{2}BC = \dfrac{1}{2}.8 = 4\\\end{array}\)
Dễ dàng suy ra \(\Delta AMN = \Delta A'B'C'\left( {c - c - c} \right)\).
Vậy \(\Delta AMN \sim \Delta A'B'C'\)(*)
Xét tam giác ABC có MN // BC \(\Rightarrow \Delta AMN \sim \Delta ABC\) (**)
Từ (*) VÀ (**) \(\Rightarrow \Delta A'B'C' \sim \Delta ABC\)
Trả lời câu hỏi Toán 8 Tập 2 Bài 5 trang 74:
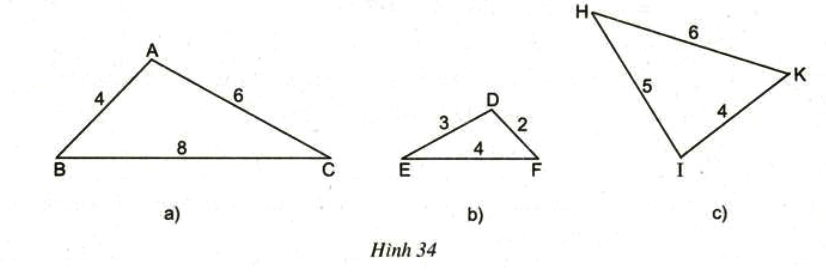
Tìm trong hình 34 các cặp tam giác đồng dạng:
Hướng dẫn giải:
Ta có tam giác \(\Delta ABC \sim \Delta DEF\)
Vì các cặp cạnh tương ứng tỉ lệ: \(\frac{{AB}}{{DF}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DE}} = 2\)
Bài 29 (trang 74, 75 SGK Toán 8 Tập 2)
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35.
Hình 35
Ta có:
\(\begin{array}{l}
\dfrac{{AB}}{{A'B'}} = \dfrac{6}{4} = \dfrac{3}{2};\,\,\dfrac{{AC}}{{A'C'}} = \dfrac{9}{6} = \dfrac{3}{2};\\\dfrac{{BC}}{{B'C'}} = \dfrac{{12}}{8} = \dfrac{3}{2}\\
\Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{3}{2}
\end{array}\)
\(\Rightarrow \Delta ABC \text{ đồng dạng }\Delta A'B'C'\left( c-c-c \right)\)
b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}} = \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}} = \dfrac{3}{2}\)
(với \(C_{ABC}\) và \(C_{A'B'C'}\) lần lượt là chu vi của hai tam giác ABC, A'B'C')
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là \(\dfrac{3}{2}\)
Bài 30 (trang 75 SGK Toán 8 Tập 2)
Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 5cm, BC = 7cm. Tam giác A'B'C' đồng dạng với tam giác A'B'C' và có chu vi bằng 55cm.
Hãy tính độ dài của các cạnh tam giác A'B'C' (làm tròn đến chữ số thập phân thứ hai).
\(\Rightarrow \Delta ABC\) đồng dạng \(\Delta A'B'C'\left( {gt} \right)\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}= \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}}\)
hay \(\dfrac{3}{A'B'} = \dfrac{7}{B'C'} = \dfrac{5}{A'C'} = \dfrac{C_{ABC}}{55} = \dfrac{3 + 7 + 5}{55} = \dfrac{{15}}{{55}} = \dfrac{3}{11}\)
(với \(C_{ABC}\) và \(C_{A'B'C'}\) lần lượt là chu vi của hai tam giác ABC, A'B'C')
\(+ )\,\,\dfrac{3}{{A'B'}} = \dfrac{3}{{11}} \Rightarrow A'B' = \dfrac{{3.11}}{3} = 11\,cm\)
\(+ )\,\,\dfrac{7}{{B'C'}} = \dfrac{3}{{11}} \Rightarrow B'C' = \dfrac{{7.11}}{3} \approx 25,67\,cm\)
\(+ )\,\,\dfrac{5}{{A'C'}} = \dfrac{3}{{11}} \Rightarrow A'C' = \dfrac{{5.11}}{3} \approx 18,33\,cm\)
Bài 31 (trang 75 SGK Toán 8 Tập 2)
Cho hai tam giác đồng dạng có tỉ số chu vi là \(\dfrac{15}{17}\) và hiệu độ dài hai cạnh tương ứng của chúng là 12,5 cm. Tính hai cạnh đó.
Giả sử ∆A'B'C' đồng dạng ∆ABC và AB-A'B'=12,5 cm.
Vì ∆A'B'C' đồng dạng ∆ABC (giả thiết) nên ta có:
\(\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}} = \dfrac{{C'A'}}{{CA}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}} = \dfrac{{C'A'}}{{CA}} = \dfrac{{A'B' + B'C' + C'A'}}{{AB + BC + CA}} = \dfrac{{{C_{A'B'C'}}}}{{{C_{ABC}}}} = \dfrac{{15}}{{17}}\)
(với \(C_{ABC}\) và \(C_{A'B'C'}\) lần lượt là chu vi của hai tam giác ABC, A'B'C')
Do đó, \(\dfrac{{A'B'}}{{AB}} =\dfrac{{15}}{{17}}\)
\(\Rightarrow \dfrac{{AB}}{{A'B'}} =\dfrac{{17}}{{15}}\)
\(\eqalign{
& \Rightarrow {{AB} \over {A'B'}} - 1 = {{17} \over {15}} - 1 \cr
& \Rightarrow {{AB - A'B'} \over {A'B'}} = {{17 - 15} \over {15}} \cr
& \Rightarrow {{12,5} \over {A'B'}} = {2 \over {15}} \cr}\)
\(\Rightarrow A'B' = \dfrac{{15}}{2}.12,5 = 93,75\,cm\)\(AB - A'B' = 12,5\,cm\)
\(\Rightarrow AB = 12,5 + 93,75 = 106,25\,\,cm\)
........................
Giải Toán 8 bài 5: Trường hợp đồng dạng thứ nhất được VnDoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, đưa ra các phương pháp định hướng giải bài và làm bài tập cụ thể, thông qua giải bài tập các em nắm chắc kiến thức môn Toán lớp 8.
Ngoài tài liệu trên, mời các bạn tham khảo thêm Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.
