Giải bài tập SBT Toán 8 bài 2: Hình thang

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 2: Hình thang được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 1: Tứ giác

Giải bài tập SBT Toán 8 bài 3: Hình thang cân

Câu 1: Tính các góc của hình thang ABCD (AB // CD), biết rằng A = 3D, B - C = 30^o.

Lời giải:

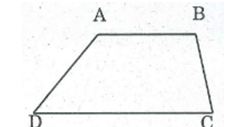
Ta có: AB // CD ⇒ A + D = 180^o (hai góc trong cùng phía)

Ta có: A = 3D (gt)

⇒ 3D + D = 180^o ⇒ D = 45^o ⇒ A = 3.45^o = 135^o

B + C = 180^o (hai góc trong cùng phía)

B - C = 30^o (gt)

⇒ 2B = 210^o ⇒ B = 105^o

C = B - 30^o = 105^o – 30^o = 75^o

Câu 2: Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. chứng minh rằng ABCD là hình thang.

Lời giải:

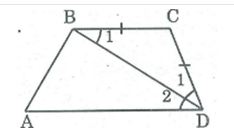
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.

⇒ ∠B1= ∠D1(tính chất tam giác cân)

Mà ∠D1= ∠D2(gt)

Suy ra: ∠B1= ∠D2

Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)

Vậy ABCD là hình thang.

Câu 3: Xem các hình dưới và cho biết:

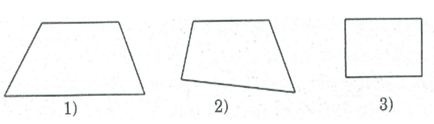
a, Tứ giác ở hình (1) chỉ có mấy cặp cạnh đối song song?

b, Tứ giác ở hình (3) có mấy cặp cạnh đối song song?

c, Tứ giác ở hình nào là hình thang?

Lời giải:

a, Tứ giác ở hình (1) chỉ có 1 cặp cạnh đối song song.

b, Tứ giác ở hình (3) có hai cặp cạnh đối song song.

c, Tứ giác ở hình (1) và hình (3) là hình thang.

Câu 4: Tính các góc B và D của hình thang ABCD, biết rằng: A = 60^o, C = 130^o

Lời giải:

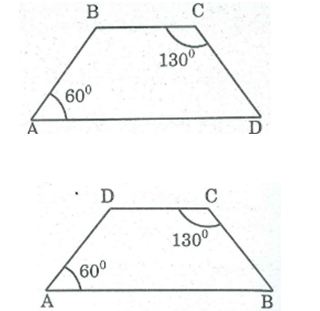
Trong hình thang ABCD, ta có A và C là hai góc đối nhau.

a, Trường hợp A và B là 2 góc kề với cạnh bên.

⇒ AB // CD

A + B = 180^o (hai góc trong cùng phía bù nhau)

⇒ B = 180^o - A = 180^o – 60^o = 120^o

C + D = 180^o (hai góc trong cùng phía bù nhau)

⇒ D = 180^o - C = 180^o – 130^o = 50^o

b, Trường hợp A và D là 2 góc kề với cạnh bên.

⇒ AB // CD

A + D = 180^o (hai góc trong cùng phía bù nhau)

⇒ D = 180^o - A = 180^o – 60^o = 120^o

C + B = 180^o (hai góc trong cùng phía bù nhau)

⇒ B = 180^o - C = 180^o – 130^o = 50^o

Câu 5: Chứng minh rằng trong hình thang có nhiều nhất là hai góc tù, có nhiều nhất là hai góc nhọn.

Lời giải:

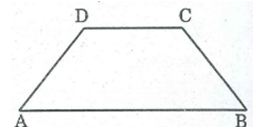
Xét hình thang ABCD có AB //CD.

Ta có:

* ∠A và ∠D là hai góc kề với cạnh bên

⇒ ∠A + ∠D = 180^o (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

* ∠B và ∠C là hai góc kề với cạnh bên

⇒ ∠B + ∠C = 180^o (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

Vậy trong bốn góc là A, B, C, D có nhiều nhất là hai góc tù và có nhiều nhất là hai góc nhọn.

Câu 6: Chứng minh rằng trong hình thang các tia phân giác của hai góc kề với một cạnh bên vuông góc với nhau.

Lời giải:

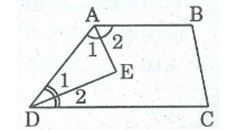
Giả sử hình thang ABCD có AB // CD

* Ta có: ∠A1= ∠A2= 12 ∠A (gt)

∠D1= ∠D2= 12 ∠D (gt)

Mà ∠A + ∠D = 180^o (2 góc trong cùng phía bù nhau)

Suy ra: ∠A1+ ∠D1= 12 (∠A1+ ∠D1) = 90^o

* Trong ΔAED, ta có:

(AED) + ∠A1+ ∠D1= 180o (tổng 3 góc trong tam giác)

⇒ (AED) = 180^o – (∠A1+ ∠D1) = 180^o - 90^o

Vậy AE ⊥ DE.

Câu 7: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E.

a, Tìm các hình thang trong hình vẽ.

b, Chứng minh rằng hình thang BDEC có một đáy bằng tổng hai cạnh bên.

Lời giải:

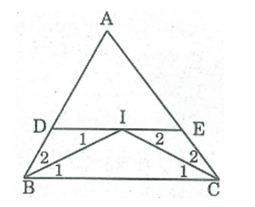
a, Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC

b, DE // BC (theo cách vẽ)

⇒ ∠I1= ∠B1(hai góc so le trong)

Mà ∠B1= ∠B2(gt)

Suy ra: ∠I1= ∠B2

Do đó: ΔBDI cân tại D ⇒ DI = DB (1)

Ta có: ∠I2= ∠C1(so le trong)

∠C1= ∠C2(gt)

Suy ra: ∠I1= ∠C2 do đó: ΔCEI cân tại E

⇒ IE = EC (2)

DE = DI + IE (3)

Từ (1), (2), (3) suy ra: DE = BD + CE

Câu 8: Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, ve tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?

Lời giải:

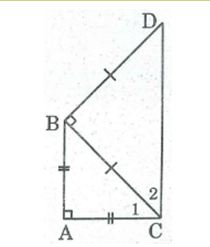
Vì ΔABC vuông cân tại A nên ∠C1= 45^o

Vì ΔBCD vuông cân tại B nên ∠C2= 45^o

∠(ACD) = ∠C1+ ∠C2= 45^o + 45^o = 90^o

⇒ AC ⊥ CD

Mà AC ⊥ AB (gt)

Suy ra: AB //CD

Vậy tứ giác ABCD là hình thang vuông.

Câu 9: Hình thang vuông ABCD có ∠A = ∠D = 90^o, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.

Lời giải:

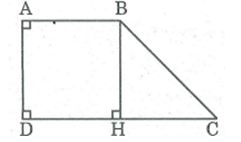
Kẻ BH ⊥ CD

Ta có: AD ⊥ CD (gt)

Suy ra: BH // AD

Hình thang ABHG có hai cạnh bên song song nên HD = AB và BH = AD

AB = AD = 2cm (gt)

⇒ BH = HD = 2cm

CH = CD – HD = 4 – 2 = 2 (cm)

Suy ra: ΔBHC vuông cân tại H ⇒ ∠C = 45o

∠B + ∠C = 180^o (2 góc trong cùng phía) ⇒ ∠B = 180^o – 45^o = 135^o

Câu 10: Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.

Lời giải:

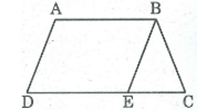
Giả sử hình thang ABCD có AB // CD

Từ B kẻ đường thẳng song song với AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE

Ta có: CD – AB = CD – ED = EC (1)

Trong ΔBEC ta có:

BE + BC > EC (bất đẳng thức tam giác)

Mà BE = AD

Suy ra: AD + BC > EC (2)

Từ (1) và (2) suy ra: AD + BC > CD – AB