Giải Toán 8 bài 3: Rút gọn phân thức

Giải SGK Toán 8 trang 38, 39, 40

Giải bài tập Toán 8 bài 3: Rút gọn phân thức

Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 38:
Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:
Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:
Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:
Bài 7 (trang 39 SGK Toán 8 Tập 1):
Bài 8 (trang 40 SGK Toán 8 Tập 1):
Bài 9 (trang 40 SGK Toán 8 Tập 1):
Bài 10 (trang 40 SGK Toán 8 Tập 1):
Bài 11 (trang 40 SGK Toán 8 Tập 1):
Bài 12 (trang 40 SGK Toán 8 Tập 1):
Bài 13 (trang 40 SGK Toán 8 Tập 1)

Giải Toán 8 bài 3: Rút gọn phân thức được VnDoc tổng hợp 13 câu hỏi bài tập kèm theo câu trả lời chi tiết rõ ràng, bám sát cheo chương trình học SGK môn Toán lớp 8. Hy vọng sẽ giúp ích cho các em có thêm tài liệu tham khảo, nâng cao kỹ năng giải Toán 8. Dưới đây là nội dung chi tiết bài học, các em tham khảo nhé.

Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 38:

Cho phân thức: $\frac{4 x^{3}}{10 x^{2} y}$ $\frac{4 x^{3}}{10 x^{2} y}$

a) Tìm nhân tử chung của cả tử và mẫu.

b) Chia cả tử và mẫu cho nhân tử chung.

Lời giải

a) Nhân tử chung của cả tử và mẫu: 2x²

b)

$\frac{4 x^{3}}{10 x^{2} y}=\frac{4 x^{3}: 2 x^{2}}{10 x^{2} y: 2 x^{2}}=\frac{2 x}{5 y}$ $\frac{4 x^{3}}{10 x^{2} y}=\frac{4 x^{3}: 2 x^{2}}{10 x^{2} y: 2 x^{2}}=\frac{2 x}{5 y}$

Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:

Cho phân thức:

$\frac{5 x+10}{25 x^{2}+50 x}$ $\frac{5 x+10}{25 x^{2}+50 x}$

a) Phân tích tử và mẫu thành nhân tử rồi tìm nhân tử chung của chúng.

b) Chia cả tử và mẫu cho nhân tử chung.

Lời giải:

a) 5x + 10 = 5(x + 2)

25x² + 50x = 25x(x + 2)

⇒ Nhân tử chung của chúng là: 5(x + 2)

b)

$\frac{5 x+10}{25 x^{2}+50 x}=\frac{(5 x+10): 5(x+2)}{\left(25 x^{2}+50 x\right): 5(x+2)}$ $\frac{5 x+10}{25 x^{2}+50 x}=\frac{(5 x+10): 5(x+2)}{\left(25 x^{2}+50 x\right): 5(x+2)}$

Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:

Rút gọn phân thức:

$\frac{x^{2}+2 x+1}{5 x^{3}+5 x^{2}}$ $\frac{x^{2}+2 x+1}{5 x^{3}+5 x^{2}}$

Lời giải

$\frac{x^{2}+2 x+1}{5 x^{3}+5 x^{2}}=\frac{(x+1)^{2}}{5 x^{2}(x+1)}=\frac{x+1}{5 x^{2}}$ $\frac{x^{2}+2 x+1}{5 x^{3}+5 x^{2}}=\frac{(x+1)^{2}}{5 x^{2}(x+1)}=\frac{x+1}{5 x^{2}}$ $\frac{3\left(x - y\right)}{y - x}$ $\frac{3\left(x - y\right)}{y - x}$

Trả lời câu hỏi Toán 8 Tập 1 Bài 3 trang 39:

Rút gọn phân thức:

$\frac{3(x-y)}{y-x}$ $\frac{3(x-y)}{y-x}$

Lời giải

$\frac{3(x-y)}{y-x}=\frac{-3(y-x)}{y-x}=-3$ $\frac{3(x-y)}{y-x}=\frac{-3(y-x)}{y-x}=-3$

Bài 7 (trang 39 SGK Toán 8 Tập 1):

Rút gọn phân thức:

$\text { a) } \frac{6 x^{2} y^{2}}{8 x y^{5}}$ $\text { a) } \frac{6 x^{2} y^{2}}{8 x y^{5}}$ $\text { b) } \frac{10 x y^{2}(x+y)}{15 x y(x+y)^{3}}$ $\text { b) } \frac{10 x y^{2}(x+y)}{15 x y(x+y)^{3}}$

$\text { c) } \frac{2 x^{2}+2 x}{x+1}$ $\text { c) } \frac{2 x^{2}+2 x}{x+1}$ $\text { d) } \frac{x^{2}-x y-x+y}{x^{2}+x y-x-y}$ $\text { d) } \frac{x^{2}-x y-x+y}{x^{2}+x y-x-y}$

Lời giải:

$\text { a) } \frac{6 \mathrm{x}^{2} \mathrm{y}^{2}}{8 \mathrm{xy}^{5}}=\frac{3 x \cdot 2 x y^{2}}{4 y^{3} \cdot 2 x y^{2}}=\frac{3 x}{4 y^{3}}$ $\text { a) } \frac{6 \mathrm{x}^{2} \mathrm{y}^{2}}{8 \mathrm{xy}^{5}}=\frac{3 x \cdot 2 x y^{2}}{4 y^{3} \cdot 2 x y^{2}}=\frac{3 x}{4 y^{3}}$

$\text { b) } \frac{10 x y^{2}(x+y)}{15 x y(x+y)^{3}}=\frac{2 y \cdot 5 x y(x+y)}{3(x+y)^{2} \cdot 5 x y(x+y)}=\frac{2 y}{3(x+y)^{2}}$ $\text { b) } \frac{10 x y^{2}(x+y)}{15 x y(x+y)^{3}}=\frac{2 y \cdot 5 x y(x+y)}{3(x+y)^{2} \cdot 5 x y(x+y)}=\frac{2 y}{3(x+y)^{2}}$

$\text { c) } \frac{2 x^{2}+2 x}{x+1}=\frac{2 x(x+1)}{x+1}=2 x$ $\text { c) } \frac{2 x^{2}+2 x}{x+1}=\frac{2 x(x+1)}{x+1}=2 x$

$\text { d) } \frac{x^{2}-x y-x+y}{x^{2}+x y-x-y}=\frac{x(x-y)-(x-y)}{x(x+y)-(x+y)}=\frac{(x-y)(x-1)}{(x+y)(x-1)}=\frac{x-y}{x+y}$ $\text { d) } \frac{x^{2}-x y-x+y}{x^{2}+x y-x-y}=\frac{x(x-y)-(x-y)}{x(x+y)-(x+y)}=\frac{(x-y)(x-1)}{(x+y)(x-1)}=\frac{x-y}{x+y}$

Bài 8 (trang 40 SGK Toán 8 Tập 1):

Trong tờ nháp của một bạn có ghi một số phép rút gọn phân thức như hình sau:

$\text { a) } \frac{3 x y}{9 y}=\frac{x}{3}$ $\text { a) } \frac{3 x y}{9 y}=\frac{x}{3}$ $\text { b) } \frac{3 x y+3}{9 y+3}=\frac{x}{3}$ $\text { b) } \frac{3 x y+3}{9 y+3}=\frac{x}{3}$

$\text { c) } \frac{3 x y+3}{9 y+9}=\frac{x+1}{3+3}=\frac{x+1}{6}$ $\text { c) } \frac{3 x y+3}{9 y+9}=\frac{x+1}{3+3}=\frac{x+1}{6}$ $\text { d) } \frac{3 x y+3 x}{9 y+9}=\frac{x}{3}$ $\text { d) } \frac{3 x y+3 x}{9 y+9}=\frac{x}{3}$

Theo em câu nào đúng, câu nào sai? Em hãy giải thích.

Lời giải:

$\text { a) } \frac{3 x y}{9 y}=\frac{x \cdot 3 y}{3.3 y}=\frac{x}{3}$ $\text { a) } \frac{3 x y}{9 y}=\frac{x \cdot 3 y}{3.3 y}=\frac{x}{3}$

Đúng vì đã chia cả tử và mẫu của vế trái cho 3y.

b) Vế phải chứng tỏ đã chia mẫu của vế trái cho 3y + 1 vì 9y + 3 = 3(3y + 1).

Nhưng tử của của vế trái không có nhân tử 3y + 1. Nên phép rút gọn này sai.

c) Sai, vì y không phải là nhân tử chung của tử thức và mẫu thức của vế trái.

d) Đúng, vì đã rút gọn phân thức ở vế trái với nhân tử chung là 3(y + 1).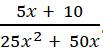
Giải bài tập SGK Toán lớp 8 bài 3: Rút gọn phân thức

Bài 9 (trang 40 SGK Toán 8 Tập 1):

Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:

$\text { a) } \frac{36(x-2)^{3}}{32-16 x}$ $\text { a) } \frac{36(x-2)^{3}}{32-16 x}$ $\text { b) } \frac{x^{2}-x y}{5 y^{2}-5 x y}$ $\text { b) } \frac{x^{2}-x y}{5 y^{2}-5 x y}$

Lời giải:

$\text { a) } \frac{36(x-2)^{3}}{32-16 x}=\frac{36(x-2)^{3}}{16(2-x)}$ $\text { a) } \frac{36(x-2)^{3}}{32-16 x}=\frac{36(x-2)^{3}}{16(2-x)}$

$=\frac{36(x-2)^{3}}{-16(x-2)}=\frac{9(x-2)^{2}}{-4}$ $=\frac{36(x-2)^{3}}{-16(x-2)}=\frac{9(x-2)^{2}}{-4}$

Hoặc $\frac{36(x-2)^{3}}{32-16 x}=\frac{36(x-2)^{3}}{16(2-x)}$ $\frac{36(x-2)^{3}}{32-16 x}=\frac{36(x-2)^{3}}{16(2-x)}$

$=\frac{36[-(2-x)]^{3}}{16(2-x)}=\frac{-36(2-x)^{3}}{16(2-x)}$ $=\frac{36[-(2-x)]^{3}}{16(2-x)}=\frac{-36(2-x)^{3}}{16(2-x)}$

$=\frac{-9(2-x)^{2}}{4}$ $=\frac{-9(2-x)^{2}}{4}$

$\text { b) } \frac{x^{2}-x y}{5 y^{2}-5 x y}=\frac{x(x-y)}{5 y(y-x)}$ $\text { b) } \frac{x^{2}-x y}{5 y^{2}-5 x y}=\frac{x(x-y)}{5 y(y-x)}$

$=\frac{-x(y-x)}{5 y(y-x)}=\frac{-x}{5 y}$ $=\frac{-x(y-x)}{5 y(y-x)}=\frac{-x}{5 y}$

Bài 10 (trang 40 SGK Toán 8 Tập 1):

Đố. Đố em rút gọn được phân thức:

$\frac{x^{7}+x^{6}+x^{5}+x^{4}+x^{3}+x^{2}+x+1}{x^{2}-1}$ $\frac{x^{7}+x^{6}+x^{5}+x^{4}+x^{3}+x^{2}+x+1}{x^{2}-1}$

Lời giải:

$\frac{x^{7}+x^{6}+x^{5}+x^{4}+x^{3}+x^{2}+x+1}{x^{2}-1}$ $\frac{x^{7}+x^{6}+x^{5}+x^{4}+x^{3}+x^{2}+x+1}{x^{2}-1}$

$=\frac{x^{6}(x+1)+x^{4}(x+1)+x^{2}(x+1)+(x+1)}{(x-1)(x+1)}$ $=\frac{x^{6}(x+1)+x^{4}(x+1)+x^{2}(x+1)+(x+1)}{(x-1)(x+1)}$

$=\frac{(x+1)\left(x^{6}+x^{4}+x^{2}+1\right)}{(x-1)(x+1)}=\frac{x^{6}+x^{4}+x^{2}+1}{x-1}$ $=\frac{(x+1)\left(x^{6}+x^{4}+x^{2}+1\right)}{(x-1)(x+1)}=\frac{x^{6}+x^{4}+x^{2}+1}{x-1}$

$=\frac{x^{4}\left(x^{2}+1\right)+\left(x^{2}+1\right)}{x-1}=\frac{\left(x^{4}+1\right)\left(x^{2}+1\right)}{x-1}$ $=\frac{x^{4}\left(x^{2}+1\right)+\left(x^{2}+1\right)}{x-1}=\frac{\left(x^{4}+1\right)\left(x^{2}+1\right)}{x-1}$

Bài 11 (trang 40 SGK Toán 8 Tập 1):

Rút gọn phân thức:

$\text { a) } \frac{12 x^{3} y^{2}}{18 x y^{5}}$ $\text { a) } \frac{12 x^{3} y^{2}}{18 x y^{5}}$ $\text { b) } \frac{15 x(x+5)^{3}}{20 x^{2}(x+5)}$ $\text { b) } \frac{15 x(x+5)^{3}}{20 x^{2}(x+5)}$

Lời giải:

a) $\dfrac{{12{x^3}{y^2}}}{{18x{y^5}}} = \dfrac{{2{x^2}.6x{y^2}}}{{3{y^3}.6x{y^2}}} = \dfrac{{2{x^2}}}{{3{y^3}}}$ $\dfrac{{12{x^3}{y^2}}}{{18x{y^5}}} = \dfrac{{2{x^2}.6x{y^2}}}{{3{y^3}.6x{y^2}}} = \dfrac{{2{x^2}}}{{3{y^3}}}$ (rút gọn cho nhân tử chung $6x{y^2}$ $6x{y^2}$)

b) $\dfrac{{15x{{\left( {x + 5} \right)}^3}}}{{20{x^2}\left( {x + 5} \right)}} = \dfrac{{3{{\left( {x + 5} \right)}^2}.5x\left( {x + 5} \right)}}{{4x.5x\left( {x + 5} \right)}} = \dfrac{{3{{\left( {x + 5} \right)}^2}}}{{4x}}$ $\dfrac{{15x{{\left( {x + 5} \right)}^3}}}{{20{x^2}\left( {x + 5} \right)}} = \dfrac{{3{{\left( {x + 5} \right)}^2}.5x\left( {x + 5} \right)}}{{4x.5x\left( {x + 5} \right)}} = \dfrac{{3{{\left( {x + 5} \right)}^2}}}{{4x}}$ (rút gọn cho nhân tử chung $5x\left( {x + 5} \right)$ $5x\left( {x + 5} \right)$)

Bài 12 (trang 40 SGK Toán 8 Tập 1):

Phân tích tử và mẫu thành nhân tử rồi rút gọn phân thức:

a) $\dfrac{{3{x^2} - 12x + 12}}{{{x^4} - 8x}}$ $\dfrac{{3{x^2} - 12x + 12}}{{{x^4} - 8x}}$

b) $\dfrac{{7{x^2} + 14x + 7}}{{3{x^2} + 3x}}$ $\dfrac{{7{x^2} + 14x + 7}}{{3{x^2} + 3x}}$

Lời giải:

a)

$\eqalign{ & {{3{x^2} - 12x + 12} \over {{x^4} - 8x}} = {{3\left( {{x^2} - 4x + 4} \right)} \over {x\left( {{x^3} - 8} \right)}} \cr & = {{3\left( {{x^2} - 2.x.2 + {2^2}} \right)} \over {x\left( {{x^3} - {2^3}} \right)}} \cr & = {{3{{\left( {x - 2} \right)}^2}} \over {x\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}} \cr & = {{3\left( {x - 2} \right)} \over {x\left( {{x^2} + 2x + 4} \right)}} \cr}$ $\eqalign{ & {{3{x^2} - 12x + 12} \over {{x^4} - 8x}} = {{3\left( {{x^2} - 4x + 4} \right)} \over {x\left( {{x^3} - 8} \right)}} \cr & = {{3\left( {{x^2} - 2.x.2 + {2^2}} \right)} \over {x\left( {{x^3} - {2^3}} \right)}} \cr & = {{3{{\left( {x - 2} \right)}^2}} \over {x\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}} \cr & = {{3\left( {x - 2} \right)} \over {x\left( {{x^2} + 2x + 4} \right)}} \cr}$

b)

$\eqalign{ & {{7{x^2} + 14x + 7} \over {3{x^2} + 3x}} = {{7\left( {{x^2} + 2x + 1} \right)} \over {3x\left( {x + 1} \right)}} \cr & = {{7{{\left( {x + 1} \right)}^2}} \over {3x\left( {x + 1} \right)}} = {{7\left( {x + 1} \right)} \over {3x}} \cr}$ $\eqalign{ & {{7{x^2} + 14x + 7} \over {3{x^2} + 3x}} = {{7\left( {{x^2} + 2x + 1} \right)} \over {3x\left( {x + 1} \right)}} \cr & = {{7{{\left( {x + 1} \right)}^2}} \over {3x\left( {x + 1} \right)}} = {{7\left( {x + 1} \right)} \over {3x}} \cr}$

(rút gọn cho nhân tử chung là x+1)

Bài 13 (trang 40 SGK Toán 8 Tập 1)

Áp dụng quy tắc đổi dấu rồi rút gọn phân thức:

a) $\dfrac{{45x\left( {3 - x} \right)}}{{15x{{\left( {x - 3} \right)}^3}}}$ $\dfrac{{45x\left( {3 - x} \right)}}{{15x{{\left( {x - 3} \right)}^3}}}$

b) $\dfrac{{{y^2} - {x^2}}}{{{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}}$ $\dfrac{{{y^2} - {x^2}}}{{{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}}$

Lời giải:

a)

$\eqalign{ & {{45x\left( {3 - x} \right)} \over {15x{{\left( {x - 3} \right)}^3}}} = {{3.15x\left( {3 - x} \right)} \over {15x{{\left( {x - 3} \right)}^3}}} \cr & = {{3\left( {3 - x} \right)} \over {{{\left( {x - 3} \right)}^3}}} = {{ - 3\left( {x - 3} \right)} \over {{{\left( {x - 3} \right)}^3}}}\cr& = {{ - 3.\left( {x - 3} \right)} \over {{{\left( {x - 3} \right)}^2}.(x-3)}}\cr& = {{ - 3} \over {{{\left( {x - 3} \right)}^2}}} \cr}$ $\eqalign{ & {{45x\left( {3 - x} \right)} \over {15x{{\left( {x - 3} \right)}^3}}} = {{3.15x\left( {3 - x} \right)} \over {15x{{\left( {x - 3} \right)}^3}}} \cr & = {{3\left( {3 - x} \right)} \over {{{\left( {x - 3} \right)}^3}}} = {{ - 3\left( {x - 3} \right)} \over {{{\left( {x - 3} \right)}^3}}}\cr& = {{ - 3.\left( {x - 3} \right)} \over {{{\left( {x - 3} \right)}^2}.(x-3)}}\cr& = {{ - 3} \over {{{\left( {x - 3} \right)}^2}}} \cr}$

b)

$\eqalign{ & {{{y^2} - {x^2}} \over {{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}} \cr & = {{\left( {y + x} \right)\left( {y - x} \right)} \over {{{\left( {x - y} \right)}^3}}} \cr & = {{ - \left( {x + y} \right)\left( {x - y} \right)} \over {{{\left( {x - y} \right)}^3}}} \,\text{(do}\,\,y-x=-(x-y))\cr & = {{ - \left( {x + y} \right)} \over {{{\left( {x - y} \right)}^2}}} \cr}$ $\eqalign{ & {{{y^2} - {x^2}} \over {{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}} \cr & = {{\left( {y + x} \right)\left( {y - x} \right)} \over {{{\left( {x - y} \right)}^3}}} \cr & = {{ - \left( {x + y} \right)\left( {x - y} \right)} \over {{{\left( {x - y} \right)}^3}}} \,\text{(do}\,\,y-x=-(x-y))\cr & = {{ - \left( {x + y} \right)} \over {{{\left( {x - y} \right)}^2}}} \cr}$

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Giải Toán 8 bài 3: Hình thang cân được VnDoc chia sẻ trên đây. Hy vọng với lời giải chi tiết cũng như bám sát vào nội dung học sẽ là tài liệu hữu ích cho các em tham khảo, hiểu bài dễ hơn từ đó học tốt môn Toán lớp 8. Chúc các em học tốt, dưới đây là một số bài tập Toán lớp 8 các em tham khảo nhé:

.........................................

Ngoài Giải Toán 8 bài 3: Rút gọn phân thức, mời các bạn tham khảo thêm Giải bài tập Toán lớp 8, Giải vở bài tập Toán 8, soạn bài 8 hoặc đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt.

	Đặt câu hỏi về học tập, giáo dục, giải bài tập của bạn tại chuyên mục Hỏi đáp của VnDoc
Hỏi - Đáp	Truy cập ngay: Hỏi - Đáp học tập