Giải bài tập SBT Toán 8 bài 10: Đường thẳng song song với một đường thẳng cho trước

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 10: Đường thẳng song song với một đường thẳng cho trước được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 8: Đối xứng tâm

Giải bài tập SBT Toán 8 bài 9: Hình chữ nhật

Giải bài tập SBT Toán 8 bài 11: Hình thoi

Câu 1: Cho đoạn thẳng AB, kẻ tia Ax bất kỳ, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C, D kẻ đường thẳng song song với BE. Chứng minh rằng đoạn thẳng AB bị chia ra ba phân bằng nhau.

Lời giải:

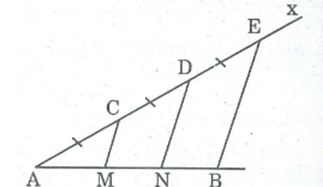
Gọi giao điểm của các đường thẳng kẻ từ C và D song song với BE cắt AB tại M và N.

Ta có: AC = CD = DE (gt)

CM // DN // BE

Theo tính chất đường thẳng song song cách đều, ta có:

AM = MN = NB

Câu 2: Cho góc vuông xOy, điểm A nằm trên tia Oy, điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào?

Lời giải:

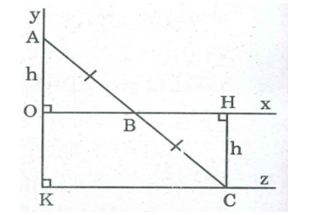
Vì điểm C đối xứng với điểm A qua điểm B nên BA = BC

Kẻ CH ⊥ Ox

Xét hai tam giác vuông AOB và CHB, ta có:

∠(AOB) = ∠(CHB ) = 90^o

BA = BC (chứng minh trên)

∠(ABO) = ∠(CBH) (đối đỉnh)

Suy ra ΔAOB = Δ CHB (cạnh huyền, góc nhọn)

⇒ CH = AO

Vì A, O cố định nên OA không đổi suy ra CH không đổi

Vì C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng bằng OA.

Khi B trung O thì C trung với điểm K đối xứng với A qua điểm O.

Vậy C chuyển động trên tia Kz // Ox, cách Ox một khoảng không đổi bằng OA.

Câu 3: Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào?

Lời giải:

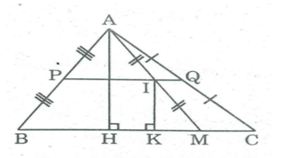
Kẻ AH ⊥ BC,IK ⊥ BC ⇒ AH // IK

Trong = ΔAHM, ta có:

AI = IM (gt)

IK // AH (chứng minh trên)

Suy ra IK là đường trung bình của ΔAHM

⇒ IK = 1/2 AH

ΔABC cố định nên AH không thay đổi ⇒ IK = 1/2 AH không đổi.

I thay đổi cách BC một khoảng bằng AH/2 không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằng AH/2

Khi M trùng với điểm B thì I trùng với điểm P là trung điểm của AB.

Khi M trùng với điểm C thì I trùng với điểm Q là trung điểm của AC.

Vậy khi M di chuyển trên cạnh BC của ΔABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của ΔABC

Câu 4: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh BC. GỌi D,E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC.

a, So sánh độ dài AM, DE.

b, Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất

Lời giải:

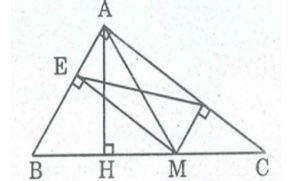
a, Xét tứ giác ADME, ta có:

∠A = 90^o (gt)

MD ⊥ AB (gt)

⇒ ∠(MDA) = 90^o

ME ⊥ AC (gt)

⇒ ∠(MEA) = 90^o

Suy ra tứ giác ADME là hình chữ nhật (vì có ba góc vuông)

⇒ AM = DE (tính chất hình chữ nhật)

b, Ta có: AH ⊥ BC nên AM ≥ AH

Dấu “=” xảy ra khi M trùng với H

Mà DE = AM (chứng minh trên)

Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC

Câu 5: Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?

Lời giải:

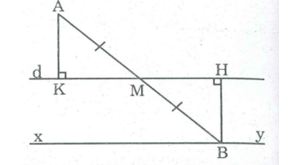
Kẻ AK ⊥ d,BH ⊥ d

Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB

Xét tam giác vuông AKM và BHM. Ta có: ∠(AKM) = ∠(BHM) = 90o

AM = MB (chứng minh trên)

∠(AMK) = ∠(BMH) (đối đỉnh)

Do đó ΔAKM = ΔAHM (cạnh huyền,góc nhọn) ⇒ AK = BH

Điểm A cố định, đường thẳng d cố định nên AK không đổi.

M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.

Câu 6: Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác AMD, BME. Trung điểm I của DE di chuyển trên đường nào?

Lời giải:

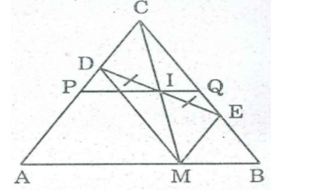
Gọi C là giao điểm của AD và BE.

Tam giác ABC có:

∠A = 60^o (vì ΔADM đều)

∠B = 60^o (vì ΔBEM đều)

Suy ra: ΔABC đều hay AB = AC = BC

Suy ra điểm C cố định.

Lại có: ∠A = ∠(EMB) = 60^o

ME // AC (vì có cặp góc đồng vị bằng nhau)

hay MD // EC

suy ra tứ giác CDME là hình bình hành.

I là trung điểm của DE nên I là trung điểm của CM

Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH

Trong ΔCHM,ta có: CI = IM và IK // CH

Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH

Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song óng với AB, cách AB một khoảng bằng 1/2 CH

Khi M trùng với A thì I trùng với trung điểm P của AC.

Khi M trùng với B thì I trùng với trung điểm Q của BC.

Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm AC, Q là trung điểm BC).

Câu 7: Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bới hai đường chéo.

Lời giải:

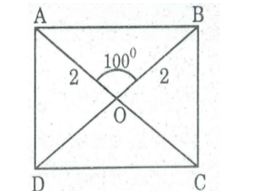
Gọi O là giao điểm của hai đường chéo AC và BD.

Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC

Lại có: AD = 1/2 AC (gt)

Suy ra: OA = OD = AD

⇒ ΔOAD đều ⇒∠(AOD ) = 60^o

Câu 8: Dựng hình chữ nhật ABCD biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 1000.

Lời giải:

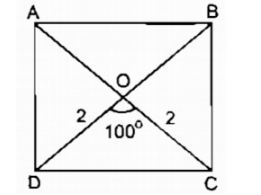
* Cách dựng:

- Dựng ΔOAB biết OA = OB = 2cm, ∠(AOB ) = 100o

- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm

- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm

Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng

* Chứng minh:

Ta có: OA = OC, OB = OD

Suy ra tứ giác ABCD là hình bình hành.

Vì AC = BD = 4 (cm) nên hình bình hành ABCD là hình chữ nhật.