Giải bài tập SBT Toán 8 bài 8: Đối xứng tâm

Bài tập môn Toán lớp 8

Giải bài tập SBT Toán 8 bài 8: Đối xứng tâm được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 8. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 8 bài 6: Đối xứng trực

Giải bài tập SBT Toán 8 bài 7: Hình bình hành

Giải bài tập SBT Toán 8 bài 9: Hình chữ nhật

Câu 1: Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm c

Lời giải:

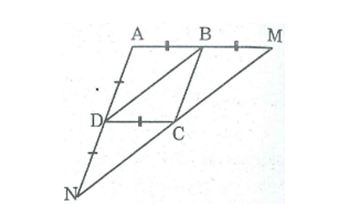
Tứ giác ABCD là hình bình hành:

⇒ AB // CD hay BM // CD

Xét tứ giác BMCD ta có:

BM // CD

BM = CD (gt)

Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ MC // BD và MC = BD (1)

AD // BC (gt) haỵ DN // BC

Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)

Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

⇒ CN // BD và CN = BD (2)

Từ (1) và (2) suy ra: M, C, N thẳng hàng và MC = CN.

Câu 2: Cho hình vẽ trong đó DE // AB, DF // AC.Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.

Lời giải:

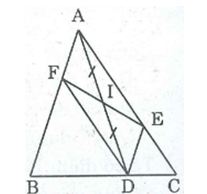
Ta có: DE //AB (gt) hay DE //AF

DF //AC (gt) hay DF //AE

Tứ giác AEDF là hình bình hành.

I là trung điểm của AD nên EF đi qua trung điểm I là IE = IP (tính chất hình bình hành)

Vậy E và F đối xứng qua tâm I.

Câu 3: Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng Với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.

Lời giải:

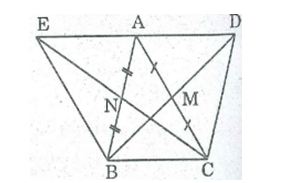
* Xét tứ giác ABCD, ta có:

MA = MC (gt)

MB = MD (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AD // BC hay AD = BC (1)

* Xét tứ giác ACBE, ta có:

AN = NB (gt)

NC = NE (định nghĩa đối xứng tâm)

Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)

Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE

Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.

Câu 4: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm A.

Lời giải:

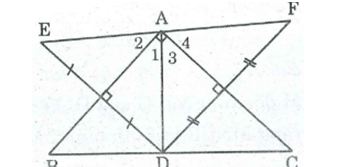
* Vì E đối xứng với D qua AB

⇒ AB là đường trung trực của đoạn thẳng DE

⇒ AD = AE (tỉnh chất đường trung trực)

Nên ΔADE cân tại A

Suy ra: AB là đường phân giác của ∠(DAE) ⇒ ∠A1= ∠A2

* Vì F đối xứng với D qua AC

⇒ AC là đường trung trực của đoạn thẳng DF

⇒ AD = AF (tính chất đường trung trực)

Nên ΔADF cân tại A

Suy ra: AC là phân giác của ∠(DAF)

⇒ ∠A3= ∠A4

∠(EAF) = ∠(EAD) + ∠(DAF) = ∠A1+ ∠A2+ ∠A3+ ∠A4= 2(∠A1+ ∠A3) = 2.90^o= 180^o

⇒ E, A, F thẳng hàng có AE = AF = AD

Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.

Câu 5: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh đối AD, BC ở E, F. Chứng minh E và F đối xứng với nhau qua điểm O.

Lời giải:

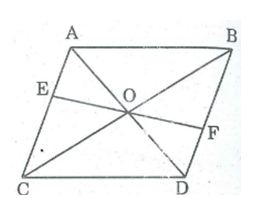
Xét ΔOED và ΔOFB, ta có:

∠(EOD)= ∠(FOB)(đối đỉnh)

OD = OB (tính chất hình bình hành)

∠(ODE)= ∠(OBF)(so le trong)

Do đó: ΔOED = ΔOFB (g.c.g)

⇒ OE = OF

Vậy O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O

Câu 6: Cho hình bên, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O

Lời giải:

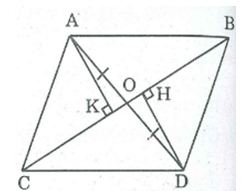
Xét hại tam giác vuông AHO và CKO, ta có:

∠(AHO)= ∠(CKO)= 90^o

OA = OC (tính chất hình bình hành)

∠(AOH)= ∠(COK)(đối đỉnh)

Suy ra: ΔAHO = ΔCKO (cạnh huyền, góc nhọn)

⇒ OH = OK

Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O

Câu 7: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D. Vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Lời giải:

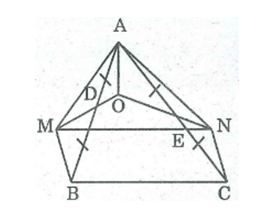
* Xét tứ giác AOBM, ta có:

DA = DB (gt)

DO = DM (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ BM // AO và BM = AO (1)

* Xét tứ giác AOCN, ta có: EA = EC (gt)

EO = EN (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ CN // AO và CN = AO (2)

Từ (1) và (2) suy ra:BM // CN và BM = CN.

Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).

Câu 8: Cho tam giácABC, các đường trungtuyến AD, BE, CF cắt nhau tại G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.

Lời giải:

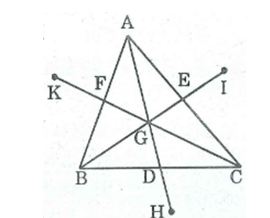
* Ta có: GD = DH (tính chất đối xứng tâm)

⇒ GH = 2GD (l)

GA = 2GD (tính chất đường trung tuyến của tam giác) (2)

Từ (1) và (2) suy ra: GA = GH

Suy ra điểm đối xứng với điểm A qua tâm G là H.

* Ta có: GE = EI (tính chất đối xứng tâm)

⇒ GI = 2GB (3)

GB = 2GE (tính chất đường trung tuyên của tam giác) (4)

Từ (3) và (4) suy ra: GB = GI

Suy ra điểm đối xứng với điểm B qua tâm G là I.

GF = FK (tỉnh chất đối xứng tâm)

⇒ GK = 2GF (5)

GC = 2GF (tính chất đường trung tuyến của tam giác) (6)

Từ (5) và (6) Suy ra: GC = GK

Suy ra điểm đối xứng với điểm C qua tâm G là điểm K

Câu 9: Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O kẻ đường thẳng cắt đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G, H. Chứng minh rằng EGFH là hình bình hành.

Lời giải:

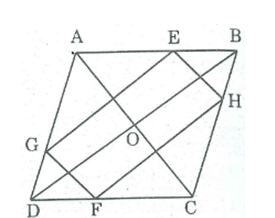
* Xét ΔOAE và ΔOCF, ta có:

OA = OC (tính chất hình bình hành)

∠(AOE)= ∠(COF)(đối đỉnh)

∠(OAE)= ∠(OCF)(so le trong)

Do đó: ΔOAE = ΔOCF (g.c.g)

⇒ OE = OF (l)

* Xét ΔOAG và ΔOCH, ta có:

OA = OC (tính chất hình bình hành)

∠(AOG) = ∠(COH)(dối đỉnh)

∠(OAG) = ∠(OCH)(so le trong).

Do đó: ΔOAG = ΔOCH (g.c.g)

⇒ OG = OH (2)

Từ (1) và (2) suy ra tứ giác EGFH là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường).

Câu 10: Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm G đối xứng với A qua Oy.

a, Chứng minh rằng OB = OC

b, Tính số đo góc xOy để B đối xứng với A qua O

Lời giải:

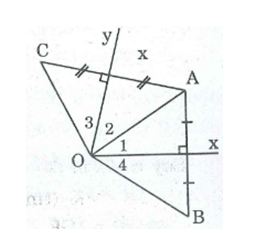
a, Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.

⇒ OA = OB (tính chất đường trung trực) (1)

Vì C đối xứng với A qua trục Ọy nên Oy là đườngtrung trực của đoạn AC.

⇒ OA = OC (tỉnh chất đường trung trực) (2)

Từ (l) và (2) suy ra: OB = OC.

b, Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng

ΔOAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của ∠(AOB) ⇒ ∠O1= ∠O3

ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của ∠(AOC) ⇒ ∠O2= ∠O4

Vì B, O, C thẳng hàng nên:

∠O1+∠O2+∠O3+∠O4 = 180^o ⇒ 2 ∠O1+ 2 ∠O2= 180^o

⇒ ∠O1+∠O2= 90o ⇒ ∠(xOy) = 90^o

Vậy ∠(xOy) = 90o thì B đối xứng với C qua tâm O