VnDoc.com

Bài tập Đồ thị của hàm số bậc nhất y = ax + b, a ≠ 0

Bài tập Toán 8 Đồ thị của hàm số bậc nhất

Bài trước

Tải về

Bài sau

Bài tập về Đồ thị của hàm số bậc nhất

A. Đồ thị của hàm số bậc nhất
B. Cách vẽ đồ thị hàm số
C. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
D. Vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy.
E. Bài tập về Đồ thị của hàm số bậc nhất

Bài tập về Đồ thị của hàm số bậc nhất gồm lí thuyết và bài tập đa dạng được phân loại từ cơ bản đến nâng cao. Tài liệu sẽ giúp các em học sinh ôn tập các kiến thức về hàm số bậc nhất,... để chuẩn bị cho các bài thi học kì đạt hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo.

A. Đồ thị của hàm số bậc nhất

– Đồ thị hàm số $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ là một đường thẳng

B. Cách vẽ đồ thị hàm số

Đồ thị của hàm số bậc nhất $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ là một đường thẳng. Do đó, để vẽ đồ thị này, ta chỉ cần xác định được hai điểm phân biệt nào đó thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.

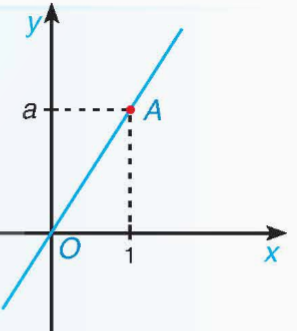
Trường hợp 1: Khi b = 0 thì $y=ax\ \left(a\ne0\right)$ $y = a x (a \neq 0)$

Đồ thị của hàm số y = ax là đường thẳng đi qua gốc tọa độ (0; 0) và điểm A(1; a).

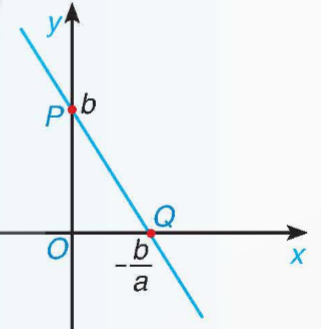
Trường hợp 2: Khi b ≠ 0 ta thường xác định hai điểm đặc biệt trên đồ thị là giao của đồ thị với hai trục tọa độ như sau:

• Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

• Cho y = 0 thì $x=-\frac{b}{a}$ $x = - \frac{b}{a}$ , ta được điểm $Q\left(-\frac{b}{a};\ 0\right)$ $Q (- \frac{b}{a}; 0)$ thuộc trục hoành Ox.

Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số $y = a x + b$ .

C. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

– Góc tạo bởi đường thẳng $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ và trục Ox.

Trong mặt phẳng Oxy, cho đường thẳng $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ . Gọi A là giao điểm của đường thẳng $y = a x + b$ và trục Ox, T là một điểm thuộc đường thẳng $y = a x + b$ và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng $y = a x + b$ và trục Ox ( hoặc nói đường thẳng $y = a x + b$ tạo với trục Ox một góc $\alpha$ $α$ )

– Hệ số góc:

Trên mặt phẳng tọa độ Oxy, cho đường thẳng $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ . Hệ số a gọi là hệ số góc của đường thẳng $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ .

D. Vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy.

Cho hai đường thẳng d: $y=ax+b\ \left(a\ne0\right)$ $y = a x + b (a \neq 0)$ và d': $y = a^{'} x + b^{'} (a^{'} \neq 0)$ .

Nếu d song song với d' thì a = a'; b ≠ b' và ngược lại.
Nếu d trùng với d' thì a = a', b = b' và ngược lại
Nếu d và d' cắt nhau thì a ≠ a' và ngược lại.

E. Bài tập về Đồ thị của hàm số bậc nhất

1. Dạng 1. Vẽ đồ thị hàm số y = ax + b (a ≠ 0)

Ví dụ 1: Vẽ đồ thị của hàm số sau: y = 2x + 1.

Lời giải:

Cho x = 0 thì y = 1, ta được giao điểm của đồ thị hàm số với trục tung Oy là P(0; 1)

Cho y = 0 thì $x=-\frac{1}{2}$ $x = - \frac{1}{2}$ , ta được giao điểm của đồ thị hàm số với trục hoành là $Q\left(-\frac{1}{2};0\right)$ $Q (- \frac{1}{2}; 0)$

Đồ thị hàm số y = 2x + 1 là đường thẳng PQ.

2. Dạng 2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Ví dụ 2: Xác định đường thẳng d: y = ax + b (a ≠ 0) biết đồ thị hàm số đi qua điểm M(1; 2) và có hệ số góc bằng 3. Xác định đường thẳng đó.

Lời giải:

Hàm số có hệ số góc bằng 3 nên a = 3 ⇒ y = 3x + b

Đồ thi hàm số có đi qua điểm M(1; 2) nên:

2 = 3 . 1 + b

⇒ b = - 1

Vậy hàm số cần tìm có dạng y = 3x - 1.

3. Dạng 3. Xét vị trí tương đối của hai đường thẳng

Ví dụ 3: Cho hai đường thẳng: (d₁): y = 2x + 1 và (d₂): y = x + 1.

a/ Chứng tỏ rằng hai đường thẳng cắt nhau.

b/ Vẽ hai đường thẳng này trên cùng một hệ trục tọa độ. Từ đó xác định tọa độ giao điểm A của hai đường thẳng đó.

c/ Xác định đường thẳng (d): y = ax + b (a ≠ 0) đi qua A và song song với đường thẳng $y = - 4 x + 2$

Lời giải:

a) Vì hai đường thẳng (d₁): y = 2x + 1 và (d₂): y = x + 1 có hệ số góc khác nhau nên hai thẳng đó cắt nhau.

b) Hình vẽ.

=> Giao điểm của hai đồ thị hàm số là điểm A(0; 1)

c) Do đường thẳng d: y = ax + b (a ≠ 0) song song với đường thẳng y = - 4x + 2

⇒ a = - 4

Đồ thị hàm số đi qua điểm A nên:

1 = - 4 . 0 + b

⇒ b = 1

Vậy đường thẳng d có dạng y = - 4x + 1

Chia sẻ, đánh giá bài viết

1

33

Bài trước

Bài sau

Chia sẻ bởi:
Ms Hoa

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!