Giải Toán 8 bài 4: Diện tích hình thang
Giải bài tập trang 125, 126 SGK Toán lớp 8 tập 1: Diện tích hình thang
Tài liệu hướng dẫn giải bài tập trang 125, 126 SGK Toán lớp 8 tập 1: Diện tích hình thang trình bày kiến thức trọng tâm của bài và gợi ý cách giải bài tập từ đó các em có thể kiểm tra, ôn tập, củng cố kiến thức đồng thời nắm vững được phương pháp, phân loại được các dạng bài tập liên quan. Hy vọng đây là tài liệu bổ ích nhất dành tặng cho các em, cùng tham khảo nhé!
Giải bài tập trang 71, 72 SGK Toán lớp 8 tập 2: Hai tam giác đồng dạng
Giải bài tập trang 79, 80 SGK Toán lớp 8 tập 1: Đường trung bình của tam giác, của hình thang
Lý thuyết diện tích hình thang
1. Công thức tính diện tích hình thang
Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
S = ½(a + b).h
2. Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
S = ah
Giải bài tập trang 125, 126 SGK Toán lớp 8 tập 1
Bài 26 trang 125 sgk toán lớp 8 tập 1
Tính diện tích hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828 m2
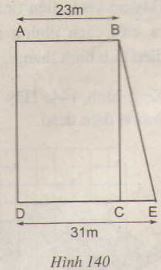
Hướng dẫn giải:
Gợi ý đáp án:
Ta có
\({S_{ABC{\rm{D}}}} = AB.A{\rm{D}} = 828{m^2}\)
\(\Rightarrow AD =\dfrac{828}{AB} =\dfrac{828}{23} = 36 \,(m)\)
Do đó diện tích của hình thang ABED là:
\({S_{ABED}} = \dfrac{{\left( {AB + DE} \right).AD}}{2} \,= \dfrac{{\left( {23 + 31} \right).36}}{2} = 972({m^2})\)
Bài 27 trang 125 sgk toán lớp 8 tập 1
Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước.
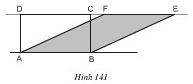
Hướng dẫn giải:
Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.
Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước:
- Lấy nột cạnh của hình bình hành ABEF làm một cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.
- Vẽ đường thẳng EF.
- Từ A và b vẽ các đường thẳng vuông góc với đường thẳng EF, chúng cắt đường thẳng EF lần lượt tại D, C. Vẽ các đoạn thẳng AD, BC. ABCD là hình chữ nhật có cùng diện tích với hình bình hành ABEF đã cho
Bài 28 trang 126 sgk toán lớp 8 tập 1
Xem hình 142 (IG// FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE.
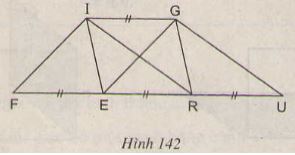
Hướng dẫn giải:
Ta có IG // FU nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h. Các hình bình hành FIGE, IGRE, IGUR có cạnh bằng nhau FE = ER = RU có cùng chiều cao ứng với cạnh đó nên diện tích chúng bằng nhau. Tức là SFIGR = SIGRE = SIGUR (h.FE)
Mặt khác các tam giác IFG, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình bình hành FIGE nên diện tích chúng bằng nhau:
SIFR = SGEU = SFIGE
Vậy SFIGE = SIGRE = SIGUR = SIFR = SGEU
Bài 29 trang 126 sgk toán lớp 8 tập 1
Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau?
Hướng dẫn giải:
Cho hình thang ABCD. Gọi M, N lần lượt là trung điểm của hay đáy AB, CD. Ta có hai hình thang AMND và BMNC có cùng chiều cao, có đáy trên bằng nhau AM = MB, có đáy dưới bằng nhau DN = NC. Vậy chúng có diện tích bằng nhau.
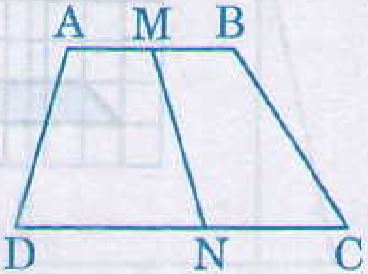
Bài 30 trang 126 sgk toán lớp 8 tập 1
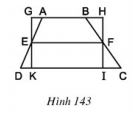
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
Hướng dẫn giải
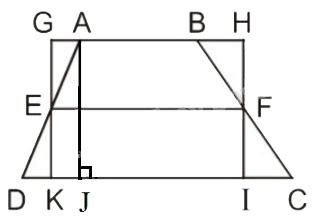
Ta có hình thang ABCD (AB // CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.
Xét hai tam giác vuông: ∆AEG và ∆DEK có:
+) AE = ED (do E là trung điểm của AD)
+) \(\widehat {A{\rm{E}}G} = \widehat {DEK}\) (đối đỉnh)
\(\Rightarrow ∆AEG = ∆DEK\) (cạnh huyền-góc nhọn)
Suy ra \({S_{AEG}}={S_{DEK}}\)
Xét hai tam giác vuông: ∆BFH và ∆CFI có:
+) BF = FC (do F là trung điểm của BC)
+) \(\widehat {B{\rm{F}}H} = \widehat {CFI}\)(đối đỉnh)
\(\Rightarrow ∆BFH = ∆CFI\) (cạnh huyền-góc nhọn)
\(\Rightarrow {S_{BFH}}={S_{CFI}}\)
Do đó \({S_{ABCD}} = {S_{AEKIFB}} + {S_{DEK}} + {S_{CFI}} \,= {S_{AEKIFB}} + {S_{AEG}} + {S_{BFH}} = {S_{GHIK}}\)
Nên:
\({S_{ABCD}} = {S_{GHIK}} =GH.HI= EF.HI\) (do GH=EF) mà \(EF = \dfrac{{AB + CD}}{2}\) (tính chất đường trung bình hình thang ABCD)
Do đó \({S_{ABCD}} = \dfrac{{AB + CD}}{2}.HI\)
Gọi AJ là chiều cao của hình thang ABCD thì AJ = HI, từ đó suy ra:
\({S_{ABCD}} = \dfrac{{AB + CD}}{2}.AJ\)
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
Bài 31 trang 126 sgk toán lớp 8 tập 1
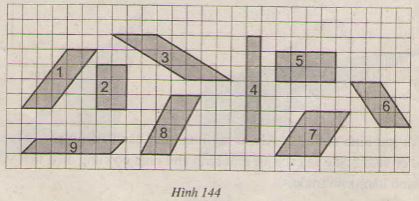
Xem hình 144. Hãy chỉ ra các hình có cùng diện tích (lấy ô vuông làm đơn vị diện tích)
Hướng dẫn giải:
Các hình 2,6,9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3, 7 có cùng diện tích là 8 ô vuông.
Hình 4 có diện tích là 7 ô vuông nên không có diện tích với một trong các hình đã cho.
........................
Giải Toán 8 bài 4: Diện tích hình thang được VnDoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho các em có thêm tài liệu tham khảo, đưa ra các phương pháp định hướng giải bài và làm bài tập cụ thể, thông qua giải bài tập các em nắm chắc kiến thức môn Toán lớp 8.
Ngoài Giải Toán 8 bài 4: Diện tích hình thang, các bạn có thể tham khảo thêm Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
