Đề thi học sinh giỏi tỉnh Nghệ An năm 2012 - 2013 môn Toán lớp 12 Bảng A (Có đáp án)

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi học sinh giỏi tỉnh Nghệ An năm 2012 - 2013 môn Toán lớp 12 Bảng A (Có đáp án).

Đề thi học sinh giỏi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH NGHỆ AN (ĐỀ THI CHÍNH THỨC)

KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 NĂM HỌC 2012 - 2013 MÔN THI: TOÁN - LỚP 12 BẢNG A (Thời gian làm bài 150 phút không kể thời gian giao đề)

Câu I: (3,0 điểm)

Cho hàm số có đồ thị (C) và điểm P(2; 5).

Tìm các giá trị của tham số m để đường thẳng d: y = -x + m cắt đồ thị (C) tại hai điểm phân biệt A và B sao cho tam giác PAB đều.

Câu II: (6,0 điểm)

1. Giải phương trình:

2. Giải hệ phương trình: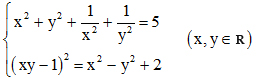

Câu III: (6,0 điểm)

1. Cho lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.

2. Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Mặt phẳng (α) đi qua trung điểm I của đoạn thẳng AG và cắt các cạnh AB, AC, AD tại các điểm (khác A). Gọi h_A, h_B, h_C, h_D lần lượt là khoảng cách từ các điểm A, B, C, D đến mặt phẳng (α).

Chứng minh rằng: .

Câu IV: (2,5 điểm)

Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm A(-1; -1) và đường tròn (T): (x - 3)² + (y - 2)² = 25. Gọi B, C là hai điểm phân biệt thuộc đường tròn (T) (B, C khác A). Viết phương trình đường thẳng BC, biết I(1; 1) là tâm đường tròn nội tiếp tam giác ABC.

Câu V: (2,5 điểm)

Cho các số thực dương a, b, c. Tìm giá trị nhỏ nhất của biểu thức sau: