Giải SBT Tin học 10 Kết nối tri thức bài 4

Với nội dung bài Giải sách bài tập Tin học 10 bài 4: Hệ nhị phân và dữ liệu số nguyên sách Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Tin học 10.

Bài: Hệ nhị phân và dữ liệu số nguyên

Câu 4.1 trang 10 SBT Tin học 10: Trong các lí do máy tính dùng hệ nhị phân, lí do nào kém xác đáng nhất?

A. Hệ nhị phân phù hợp với việc lưu trữ dữ liệu trong máy tính bằng dãy bit.

B. Việc thực hiện các phép tính số học trong hệ nhị phân khá đơn giản, dễ thực hiện hơn trên máy tính.

C. Hệ nhị phân là hệ đếm có cơ số nhỏ nhất.

D. Các trạng thái nhị phân cũng phù hợp với việc thể hiện đầu vào/đầu ra theo kiểu đóng mở của các mạch điện tử, được dùng làm cơ sở thiết kế các mạch điện xử lí các dữ liệu nhị phân.

Trả lời:

Đáp án đúng là: C

Hệ đếm nhị phân được dùng cho máy tính không phải vì lí do nó là hệ đếm có cơ số nhỏ nhất.

Câu 4.2 trang 10 SBT Tin học 10: Em hãy đổi biểu diễn các số sau từ hệ thập phân sang hệ nhị phân:

a) 14

b) 125

c) 217

d) 321

Trả lời:

a) 14₍₁₀₎ = 1110₍₂₎

b) 125₍₁₀₎ = 1111101₍₂₎

c) 217₍₁₀₎ = 11011001₍₂₎

d) 321₍₁₀₎ = 101000001₍₂₎

Câu 4.3 trang 10 SBT Tin học 10: Đổi biểu diễn các số sau từ hệ nhị phân sang hệ thập phân:

a) 10011.

b) 110111.

c) 1101101.

d) 10100010.

Trả lời:

a) 10011₍₂₎ = 1 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰ =19

b) 110111₍₂₎ = 55

c) 1101101₍₂₎ = 109

d) 10100010₍₂₎ = 162

Câu 4.4 trang 10 SBT Tin học 10: Thực hiện các phép tính cộng sau đây trong hệ nhị phân:

a) 11001 + 10110.

b) 101110 + 110001.

c) 1011001 + 1101.

d) 1100111 + 10110.

Trả lời:

Chú ý: Phép cộng cũng được thực hiện tương tự như trong hệ thập phân, thực hiện từ phải qua trái.

a) 11001 + 10110 = 101111

b) 101110 + 110001 = 1011111

c) 1011001 + 1101= 1100110

d) 1100111 + 10110 = 1111101

Câu 4.5 trang 10 SBT Tin học 10: Thực hiện các phép cộng theo quy trình sau:

- Đổi dữ liệu từ hệ thập phân sang hệ nhị phân.

- Cộng trong hệ nhị phân.

- Đổi kết quả từ hệ nhị phân về hệ thập phân.

a) 17 + 25.

b) 29 + 37.

c) 101 + 26.

d) 175 + 46.

Trả lời:

a) 17 + 25 ► 10001 +11001 = 101010 ► 42

b) 29 + 37 ► 11101 + 100101 = 1000010 ► 66

c) 101 + 26 ►1100101 + 11010 = 1111111 ► 127

d) 175 + 46 ►10101111 + 101110 = 11011101 ► 221

Câu 4.6 trang 11 SBT Tin học 10: Thực hiện các phép tính nhân sau đây trong hệ nhị phân:

a) 110 × 101.

b) 1011 × 1101.

c) 10101 × 1001.

d) 11001 × 10110.

Trả lời:

a) 110 × 101 = 11110

b) 1011 × 1101 = 10001111

c) 10101 × 1001 = 10111101

d) 11001 × 10110 = 1000100110

Câu 4.7 trang 11 SBT Tin học 10: Thực hiện các phép nhân theo quy trình sau:

- Đổi dữ liệu từ hệ thập phân sang hệ nhị phân.

- Nhân trong hệ nhị phân.

- Đổi kết quả từ hệ nhị phân về hệ thập phân.

a) 7 × 5.

b) 29 × 3.

c) 21 × 6.

d) 75 × 3.

Trả lời:

a) 7 × 5 ► 111 × 101 = 100011 ► 35

b) 29 × 3 ► 11101 × 11 = 1010111 ► 87

c) 21 × 6 ► 10101 × 110 = 1111110 ► 126

d) 75 × 3 ► 1001011 × 11= 11100001 ► 225

Câu 4.8 (*) trang 11 SBT Tin học 10: Máy tính không làm việc trực tiếp với hệ thập phân mà làm việc trong hệ nhị phân. Biểu diễn trong hệ nhị phân thường dài gấp 3 lần trong hệ thập phân, lại rất dễ nhầm lẫn. Người làm tin học thường làm việc với hệ đếm cơ số 16, còn gọi là hệ hexa. Em hãy tìm hiểu hệ hexa theo các gợi ý sau:

- Ngoài các chữ số truyền thống như 0, 1, 2, ..., 9 thì hệ hexa còn dùng những chữ số nào?

- Giá trị tương ứng của các chữ số trong hệ hexa tương ứng với các giá trị nào trong hệ thập phân và hệ nhị phân?

- Cách đổi biểu diễn giữa hệ nhị phân và hệ hexa.

Trả lời:

- Ngoài các chữ số truyền thống 0, 1, 2, ..., 9, hệ hexa còn dùng các chữ số mở rộng A, B, C, D, E, F có giá trị tương ứng với 10, 11, ..., 15 mà mỗi chữ số của hệ hexa thể hiện trong hệ nhị phân và hệ thập phân như sau:

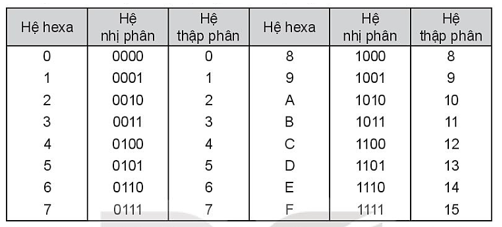
- Mỗi số đều có thể biểu diễn duy nhất trong hệ hexa bởi một dãy các chữ số của hệ hexa, một chữ số ở một hàng nào đó sẽ có giá trị gấp 16 lần chữ số đó ở hàng liền kề bên phải.

- Ví dụ 9BE sẽ có giá trị là 9 × 16² + 11 × 16 + 14 = 2494.

- Để đổi một số trong hệ hexa sang hệ nhị phân, em thay mỗi chữ số của số trong hệ hexa bởi đủ 4 chữ số của hệ nhị phân.

- Ngược lại, để đổi một số từ hệ nhị phân sang hệ hexa, kể từ dấu phẩy, tách thành từng nhóm đủ 4 chữ số nhị phân (nếu cần bổ sung thêm các chữ số 0 vào hai phía cho đủ 4 chữ số mỗi nhóm) rồi thay mỗi nhóm ấy bằng một chữ số của hệ hexa.

Ví dụ 110011011,111011 sẽ được tách thành 0001|1001|1011,1110|1100 và đổi thành 19B,EC.

Câu 4.9 (*) trang 11 SBT Tin học 10: Trò chơi đoán ngày trong tháng.

An bảo Bình, cậu hãy nghĩ đến một ngày trong tháng, tớ hỏi đúng 5 câu, cậu chỉ được trả lời đúng hay sai là tớ biết ngày cậu nghĩ. Bình nghĩ số 25.

- An hỏi: số đó bé hơn 16? Bình bảo Sai, An ghi vào sổ tay số 1.

- An hỏi: số đó bé hơn 24? Bình bảo Sai, An ghi vào sổ tay tiếp một số 1 nữa thành 11.

- An hỏi: số đó bé hơn 28? Bình bảo Đúng, An ghi vào sổ tay tiếp nhưng là số 0 thành 110. (Cứ nói sai là ghi 1, nói đúng là ghi 0).

- An hỏi: Số đó bé hơn 26? Bình bảo Đúng, An ghi vào sổ tay tiếp số 0 thành 1100.

- An hỏi: Số đó bé hơn 25? Bình bảo Sai, An ghi vào sổ tay tiếp số 1 thành 11001 và bảo số cậu nghĩ là 25, đây này 11001 chẳng phải là 25 trong hệ thập phân sao. Bình không hiểu tại sao lại thế. Em có thể giải thích cho Bình được không?

Trả lời:

Cách hỏi của An nhằm xác định từng chữ số trong biểu diễn nhị phân của số.

- Xét các số nhị phân có 5 chữ số. Số nhỏ nhất là 00000 là 0₍₁₀₎ và lớn nhất là 11111 là 31₍₁₀₎.

- Một số nhị phân có biểu diễn d₄d₃d₂d₁d₀ sẽ có giá trị là:

d₄ × 16 + d₃ × 8 + d₂ × 4 + d1 ×2 + d0.

- Vì thế nếu một số nằm trong khoảng từ 0 đến 31 mà nhỏ hơn 16 thì d4 phải là 0, ngược lại sẽ là 1. Vì thế câu hỏi đầu tiên của An nhằm xác định d4. (d4 = 1 vì số đã nghĩ không nhỏ hơn 16).

- Đối với d3, cần xác định số còn lại sau khi trừ đi 16, là nhỏ hơn 8 hay ngược lại. Điều này tương đương với việc xác định số đó có nhỏ hơn 16 + 8 = 24 hay không. (d3 = 1 vì số đã nghĩ không nhỏ hơn 24).

- Đối với d2 cần xác định số còn lại sau khi trừ đi 16 + 8, là nhỏ hơn 4 hay ngược lại. Điều này tương đương với việc xác định số đó nhỏ hơn 16 + 8 +4 = 28 hay không. (d2 = 0 vì số đã nghĩ nhỏ hơn 28).

- Đối với d₁ khi d₂ đã bằng 0 thì số chỉ có dạng d₄ × 16 + d₃ × 8 + d₁ × 2 + d₀ thì câu hỏi tiếp theo cần xác định số còn lại sau khi trừ đi 16 + 8 là nhỏ hơn 2 hay ngược lại. Điều này tương đương với việc xác định số đó nhỏ hơn 26 hay không. (d₁ = 0 vì số đã nghĩ nhỏ hơn 26).

- Còn với d₀, do d₁ = 0 nên lúc này số chỉ còn có dạng d₄ × 16 + d₃ × 8 + d0 thì câu hỏi tiếp theo cần xác định số còn lại sau khi trừ đi 16 + 8 là nhỏ hơn 1 hay ngược lại. Điều này tương đương với việc xác định số đó nhỏ hơn 25 hay không. (d₀ = 1 vì số đã nghĩ không nhỏ hơn 25).

⇒ Vậy chúng ta đã xác định được biểu diễn nhị phân của số Bình nghĩ.

>>> Bài tiếp theo: Giải SBT Tin học 10 Kết nối tri thức bài 5

Trên đây là toàn bộ lời giải Giải SBT Tin học lớp 10 bài 4: Hệ nhị phân và dữ liệu số nguyên sách Kết nối tri thức. Các em học sinh tham khảo thêm Tin học 10 Chân trời sáng tạo và Tin học lớp 10 Cánh Diều. VnDoc liên tục cập nhật lời giải cũng như đáp án sách mới của SGK cũng như SBT các môn cho các bạn cùng tham khảo.