Đề thi học sinh giỏi Giải toán trên Máy tính cầm tay cấp tỉnh Gia Lai môn Toán lớp 12 (2010 - 2011)

Vndoc.com xin gửi đến các bạn: Đề thi học sinh giỏi Giải toán trên Máy tính cầm tay cấp tỉnh Gia Lai môn Toán lớp 12 (2010 - 2011).

Đề thi học sinh giỏi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO GIA LAI (Đề thi chính thức)

KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY NĂM HỌC 2010 - 2011 MÔN: TOÁN LỚP 12 THPT (Thời gian làm bài 150 phút không kể thời gian giao đề)

Bài 1: (5 điểm).

Tìm tọa độ các điểm cực trị của đồ thị hàm số

Bài 2: (5 điểm).

Cho hình thang ABCD có đường chéo AC = 7, BD = 5, cạnh đáy CD = 1, góc giữa hai đường th ẳng AC và BD bằng 15⁰. Tính độ dài cạnh đáy AB.

Bài 3: (5 điểm).

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 4: (5 điểm).

Tính gần đúng nghiệm (độ, phút, giây) của phương trình

Bài 5: (5 điểm).

Giải hệ phương trình: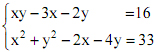

Bài 6: (5 điểm).

Cho hai đường tròn có bán kính bằng nhau và bằng 1, chúng đi qua tâm của nhau. Tính diện tích phần chung của hai hình tròn đó.

Bài 7: (5 điểm).

Tính các cạnh của hình hộp chữ nhật biết thể tích của nó bằng 15,625; diện tích toàn phần bằng 62,5 và các cạnh lập thành một ấp số nhân.

Bài 8: (5 điểm).

Trong hộp có 100 viên bi được đánh số từ 1 đến 100. Chọn ngẫu nhiên đồng thời 3 viên. Tính xác suất của biến cố: "Tổng 3 số trên 3 viên bi là một ố chia hết cho 3"

Bài 9: (5 điểm).

Trong mặt phẳng tọa độ Oxy, cho elip và đường thẳng (d ) : y = 2010x + 2011

a) Tìm tọa độ giao điểm A và B của (E) và (d).

b) Tìm tọa độ điểm M trên (E) sao cho tam giác MAB có diện tích lớn nhất.

Bài 10: (5 điểm).

Cho dãy số {X_n}, n thuộc N* được xác định như sau: x₁ = 2/3 và

Tính tổng của 2010 số hạng đầu tiên.